§ 1. Описание явлений

Встречаются различные по сложности уровни описания.

Форма и характеристики явления достаточны просты, чтобы их можно было удовлетворительно описать с помощью некоторого числа более или менее явных и легко представляемых в численном виде переменных.

Форма явления достаточно сложна, чтобы воспрепятствовать если не количественному описанию его, то по крайней мере удобной характеристике его значимых составляющих.

Наконец, явление может быть недоступно непосредственному наблюдению, и присутствие его может быть замаскировано другими сложными и независимыми явлениями.

Каждому из этих трех уровней свойственны свои типичные методы обработки, причем некоторые из них совсем недавно введены в физиологию.

А. Числовое преобразование переменных

Как мы видели, физиологические данные получают и хранят главным образом в форме зарегистрированных явлений, амплитуда которых изменяется во времени и которые объективируются в виде графических кривых разной степени сложности, поддающихся тем не менее описанию с помощью определения параметров времени, амплитуды и - дополнительно - формы.

а) Измерение времени не представляет в целом особых затруднений. Оно может осуществляться:

- либо с помощью измерения длины документа-записи; точность измерений зависит в таком случае от скорости записи явлений (развертки) и от толщины линии записи;

- либо путем непосредственного измерения временных интервалов, разделяющих два последовательных сигнала. Точность измерения зависит, разумеется, от четкости регистрации временных интервалов и точности используемых часов. Эти измерения могут быть непосредственно перенесены на шкалы и счетчики или же могут быть представлены в виде импульсов, хранящихся в целях их дальнейшей обработки либо на магнитной или перфорированной ленте, либо на механографической карте, либо в ячейках запоминающих устройств на ферромагнитных сердечниках.

б) Измерения амплитуды производятся более сложно, особенно в случаях, когда непосредственное измерение ее величины на графике-записи оказывается почему-либо недостаточным. Автоматическое определение амплитуды ставит проблему числовой транскрипции или цифрового представления величины пикового напряжения явлений. Различными способами эта проблема сводится к сравнению измеряемого напряжения с эталонным напряжением (принцип электронных вольтметров). Цифровое представление осуществляется с помощью измерения времени, необходимого для того, чтобы линейно возрастающее эталонное напряжение достигло величины изменяемого напряжения. Другой способ состоит в подсчете числа делений, необходимых для того, чтобы устройство, осуществляющее равномерное возрастание напряжения, привело эталонное напряжение к уровню, который надо измерить (см. рис. 8).

в) Характеристика формы полученных кривых может быть осуществлена с помощью различных способов в зависимости от поставленной цели, требуемой точности или предполагаемых приемов дальнейшей обработки.

Определение площади под кривой может быть осуществлено либо вручную, методами планиметрии, либо - более удобно и точно - с помощью электронного интегрирования (заряд емкости) предварительно выпрямленной кривой. Этот прием был применен Дэвисом (1942) для количественного описания элект-ромиограмм: заряд, поглощенный емкостью в заданную единицу времени, позволяет представить ЭМГ в виде пилообразной кривой с зубцами различной амплитуды, являющейся результатом суммирования сложных явлений, лежащих в ее основе. Еще более удовлетворительный способ (Дрогоцки, 1961, 1962) состоит в том, чтобы вызывать разряд емкости только тогда, когда накопленное напряжение достигает заданного уровня, в результате чего изменение кривой удается представить в виде более или менее быстрых колебаний разряда; преимущество этого метода в том, что мы получаем непосредственно используемые числовые параметры. Точность этих определений, разумеется, будет зависеть в первом случае от установленного для интегрального анализа времени разряда, а во втором - от выбранного эталонного напряжения (см. рис. 8).

Идентификация характерных точек кривой и их распределение во времени будет способствовать определению формы явления:

- пересечение с осью времени (точка изменения знака) дает возможность измерить частоту периодического явления;

- пики напряжения (точки изменения направления явления);

- точки перегиба (точки нулевого ускорения).

Все эти точки помогают выразить изменение явления в единицах времени (см. рис. 8).

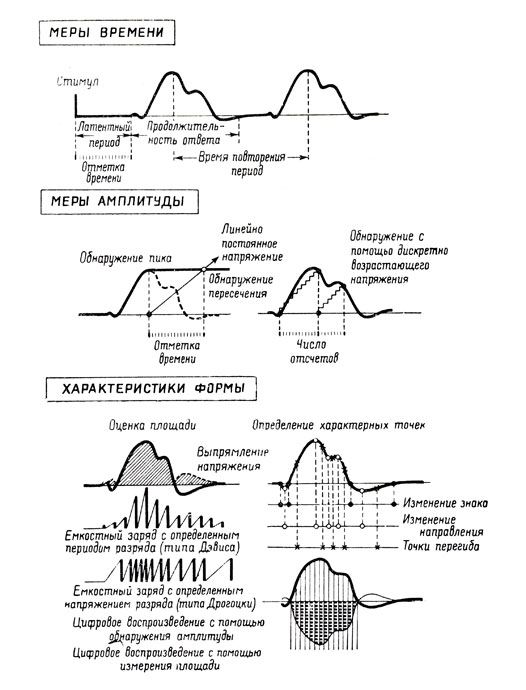
Рис. 8. Различные способы характеристики переменных (см. объяснения в тексте)

Временное квантование кривой и измерение амплитуд, соответствующих каждой выбранной точке, приводят к полному "цифровому представлению" кривой и, следовательно, к ее точному числовому определению (принцип аналого-цифрового представления).

Это говорит о широких возможностях, открывающихся в настоящее время в области численного представления данных в форме импульсов, хранимых и используемых в дальнейшем в целях более или менее сложной математической обработки.

Б. Анализ формы сложной волны

Он приобретает особое значение в случае определенных физиологических явлений. Формы полученных волн зачастую очень сложны (например, ЭЭГ). Хотя практически все полезные данные преобразуются в числа способами, которые мы только что описали, увеличение их количества не позволяло до последнего времени эффективно использовать их. В настоящее время эта проблема предстает в совершенно ином свете благодаря введению быстродействующих счетных устройств, которые позволяют производить математическую обработку волн такой формы и выявлять при этом параметры, с помощью которых становится возможным совершенно новое их описание.

Эти волны в каждом конкретном случае могут быть представлены либо систематическими функциями, для которых характерна воспроизводимость их во времени (периодические явления) (к ним относятся также функции, которые посредством аппроксимаций можно привести к систематическому виду), либо случайными функциями.

Поиски линейной характеристики этой функции, то есть такой характеристики, при которой общий ответ системы был бы равен сумме частных ответов составляющих ее элементов, представляют особый интерес в свете стремительного развития математических методов обработки линейных систем.

К сожалению, наиболее часто применяемая модель - это модель, использующая случайные функции, обработка которых много сложнее. Однако создание приемов обработки информации, совместимых с анализом линейных систем, позволяет надеяться на успех в этой области.

Мы не претендуем здесь на раскрытие этой проблемы и поэтому рекомендуем для более тщательного ознакомления с ней, например, совместную работу Дерна и Уолша (1964). Важность и размах, который приобретает в настоящий момент эта совсем новая область анализа физиологических показателей, оправдывают тем не менее этот короткий экскурс в область математических моделей, применение которых становится все более широким и находит отражение во внушительном числе недавно вышедших работ.

а) Обработка систематических функций. Гармонический анализ. Эти функции отражают систематический периодический характер воспроизведения изучаемого явления. Они могут находить свое выражение в форме так называемых синусоидальных функций. С помощью переменных (амплитуда, частота, фаза) можно охарактеризовать кривые ответа системы. Синусоидальные функции интересны тем, что их сумма, производная и интеграл также являются синусоидальными функциями той же частоты.

Линейность системы осуществляется только в том случае, если коэффициенты дифференциальных уравнений, описывающих ее, постоянны. В физиологических системах это наблюдается очень редко, поэтому так велико значение методов аппроксимирования, с помощью которых можно представить такие системы в виде линейной модели.

Схематически можно предложить три способа разложения сложных кривых, позволяющие подвергнуть их точному математическому анализу: разложение на синусоиды, на экспоненциальные и на ступенчатые функции.

Первый способ, более известный под названием "разложение в ряд Фурье", используется очень широко, и только он один будет рассмотрен здесь.

Всякую периодическую функцию, иначе говоря, такую функцию, значение которой повторяется через определенный интервал времени Т, называемый ее периодом, то есть f(t-T] =/(/), можно разложить в ряд Фурье:

f(t)=a₀/2+а₁cosω₀t+a₂cos2ω₀t+...+а_ncosnω₀t+b₁sinω₀t+b₂sin2ω₀t+...+b_nsinnω₀t ω₀=2π/T

Это означает, что сложную кривую можно рассматривать как сумму синусоидальных элементарных компонентов с частотой ω₀, 2ω₀, 3ω₀ и т. д. и амплитудой а₁, а₂,..., b₁, b₂.. . Как следствие этого кривую можно представить в виде спектра частот. Этим приемом особенно часто пользовались при первых попытках анализа электроэнцефалограмм (гармонический анализ).

Математические операции разложения в ряд Фурье могут быть заменены батареей избирательных фильтров (принцип анализатора Грея Уолтера). Однако они применимы, строго говоря, Только тогда, когда функция периодична (что, разумеется, не имеет места в случае ЭЭГ) и общая энергия функции (сумма квадратов ее амплитуд) конечна (в случае ЭЭГ она со временем возрастает). Необходимо также подчеркнуть и другую особенность: вычисления должны производиться в ограниченный период времени, что обязательно устанавливает верхний предел точности анализа частот (иллюзорными и даже опасными становятся, следовательно, попытки увеличения точности фильтрации за счет сужения полосы пропускания).

Можно также прибегнуть к разложению одного сегмента сложной кривой, считая в первом приближении этот сегмент одним циклом периодической функции. Для этого прибегают к разложению на синусоидальные функции в соответствии с преобразованием Фурье; математически такое разложение представляет собой интеграл ряда Фурье, Фактически эта операция сводится к преобразованию функции времени в функцию частоты, в результате чего кривая амплитуды явления перестает быть функцией времени и становится функцией частоты; мы получаем спектр амплитуды рассматриваемой функции.

Практические трудности, с которыми приходится сталкиваться при строгом применении этих методов, часто ведут к тому, что экспериментаторы не пользуются гармоническим анализом, а охотнее прибегают к более удобному моделированию случайными функциями.

б) Обработка случайных функций. Спектральный анализ. Смысл его состоит в том, что подыскиваются "некоторые" функции, с помощью которых можно описать "случайные" явления, с тем чтобы таким образом подвергнуть их математическому анализу. Мы вступаем здесь, разумеется, в хорошо знакомую психологу область статистических определений, по крайней мере в том, что касается дискретных переменных величин. Действительно, можно определить распределение вероятностей, если переменная х принимает конечное число дискретных значений.

Для непрерывных переменных величин определяют функцию плотности вероятности, которая является производной от ее функции распределения. Заметим, что гауссово распределение такой кривой служит правилом для большинства случайных переменных величин типа фонового шума. Среднее значение, среднее квадратическое отклонение и стандартное отклонение представляют собой характеристики, служащие основой для описания случайных функций.

В биологических экспериментах проблема приобретает новый аспект в результате введения переменной времени, оказывающей влияние на эволюцию формы сложной волны. Причем речь уже идет не о случайной функции, а о случайном процессе. Интересная ситуация возникает, когда характеристики этого процесса не зависят от начального момента времени. В таких случаях говорят, что имеет место стационарный случайный процесс, обладающий особым свойством, называемым эргодичностью (свойством среднего значения всех интервалов времени с вероятностью 1 быть равным среднему значению всех возможных выбранных функций в данный момент времени).

Если эти условия соблюдены, можно вычислить функцию автокорреляции процесса. Она представляет собой среднее значение произведения значений случайного процесса в два различных момента времени t₁ и t₂.

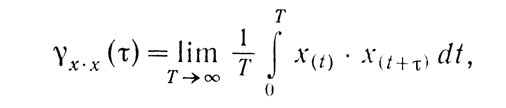
где τ есть запаздывание (t₂-t₁), а индекс х•х показывает, что вычисления относятся к той же самой функции x(_t), откуда и название - автокорреляция. Заметим, что

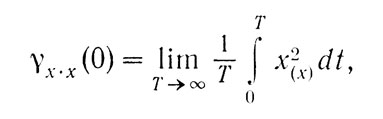
то есть для запаздывания, равного нулю, эта функция равна средней энергии функции x(_t).

Для некоторого запаздывания τ, γx•x(τ) измеряет статистическую связь, существующую между явлением в момент t и в момент t+τ. Эта связь убывает, если т возрастает и становится практически равной нулю начиная с некоторого значения τ.

С другой стороны, эта функция не зависит от момента, в который она рассматривается (стационарность), и зависит только от τ. Ее можно считать мерой скорости изменения функции, являющейся компонентой случайного процесса или, в другой форме, мерой частотной компоненты исходной функции (рис. 9).

Функция плотности спектра позволяет наилучшим образом отразить частотный состав исходной функции. Она представляет собой Фурье-преобразование функции автокорреляции. Она играет столь же важную роль для описания частотных компонентов исходной волны, как функция плотности вероятности для описания амплитудного состава волны; спектральная плотность - это представление распределения энергии в зависимости от частоты. Фоновый шум с постоянным значением функции плотности спектра для всех частот называется белым шумом.

Функция взаимной корреляции, или интеркорреляции, используется для сравнения двух случайных процессов

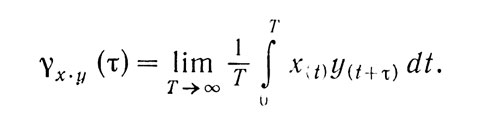
Ею измеряется статистическая связь между двумя функциями x(_t) и у (_t). Это выражение предполагает наличие канала передач или фильтра, соединяющего х и у. Функцию переноса этого фильтра можно определить как Н(_r).

Показано, что если x(_t) и у(_t) - случайные функции, то функцию переноса можно выразить отношением

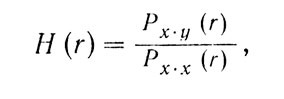
где Р_x•у означает Фурье-преобразование функции взаимной корреляции х•у, а Р _x•у - Фурье-преобразование функции автокорреляции х.

Преобразование Фурье этой функции взаимной корреляции представляет собой взаимную функцию плотности спектра. Эти последние функции позволяют, например, показать, что кривая у(_t), полученная с одного электрода, соответствует в среднем кривой x(_t), полученной с другого электрода, с запаздыванием, вызванным передачей. Изучение взаимной функции спектральной плотности дает сведения о преимущественных частотах, на которых осуществляется это соответствие. Можно вычислить также функцию передачи H(_r), являющуюся параметром фильтра, эквивалентного церебральной ткани, разделяющей два электрода.

Эти математические методы открывают широкие перспективы для анализа таких сложных явлений, как электроэнцефалограмма и электромиограмма. Они позволяют также по-новому охарактеризовать типы временной эволюции некоторых физиологических параметров (рис. 9). Нельзя, однако, недооценивать ограниченности гипотез, которые можно предложить с помощью этих методов, особенно в отношении устойчивости кривой. Однако постоянство изучаемых явлений может быть обеспечено большей частью только на короткие периоды времени, что предполагает ограниченное время вычисления. Отсюда необходимость прибегать к оценке допущенных ошибок измерения, что ставит перед нами как теоретически, так и практически еще плохо изученные проблемы.

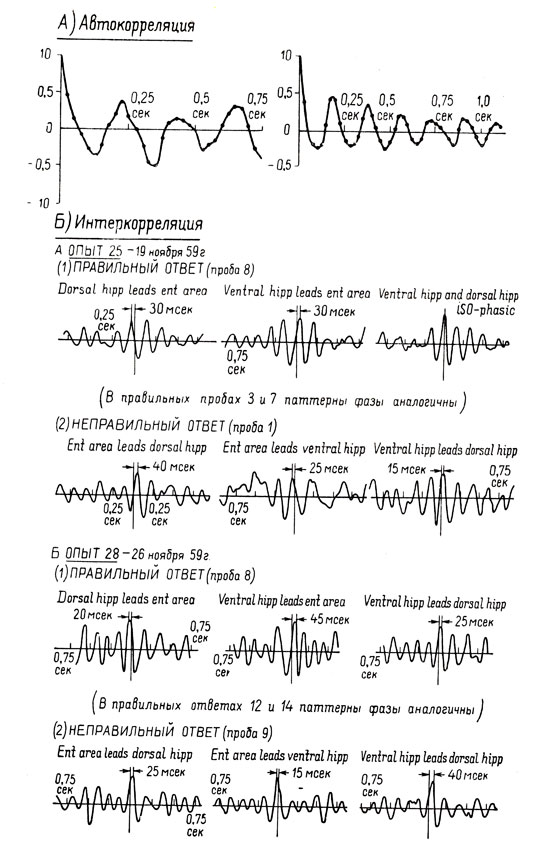
Рис. 9. Вверху: Автокорреляционный анализ кривой, полученной с помощью электродов, вживленных в область гиппокампа кошки в период ожидания предшествующий предъявлению стимулов (левая кривая), и в период раличения, начавшийся в момент предъявления стимула (правая кривая). В результате анализа удалось выявить неправильный ритм с доминирующей частотой 4 гц в период ожидания и правильный ритм с доминирующей частотой 6 гц в период различения. Внизу: Интеркорреляционный анализ (анализ взаимных корреляций) кривых, полученных с помощью электродов, вживленных в различные области обонятельного мозга: дорсальный гиппокамп (dorsal hipp); вентральный гиппокамп (ventral hipp) и энторинальную зону (ent. area) в ходе опыта по научению кошки дифференцировке. Анализ позволяет определить направление и величину сдвига фаз кривых, полученных от разных отведений. Наблюдается полная инверсия направления сдвига фаз в зависимости от правильности (1 и 3 строки) и неправильности (2 и 4 строки) реакций животного. Необходимо отметить стабильность результатов для различных групп ответов, наблюдавшихся в течение двух экспериментов, проводившихся с 7-дневным перерывом (по Эйди и сотр., 1961)

в) Выделение замаскированных сигналов в случайном явлении. Некоторые методы, разработанные в теории связи, предлагают различные способы обнаружения отдельных явлений, скрытых в сложном фоновом шуме.

Два вида этих методов можно с успехом использовать в целях обнаружения физиологических сигналов, скрытых внутри сложного явления и недоступных поэтому непосредственному изучению.

а) Распознавание типа (pattern recognition) применяется при обнаружении в случайном фоновом шуме скрытого сигнала, форма и длительность которого известны заранее. С помощью так называемого метода "согласованных фильтров" удается, например, автоматически опознавать на электрофизиологической кривой какого-либо явления характерные для него сигналы (например, патологические). Мы находим интересные применения этого метода в медицинской диагностике (Толль, 1964).

б) Изучение вызванных ответов касается систем, характеризующихся чисто случайной деятельностью, которую соотносят с набором стимулов, причем ответ на каждый из них выражается в виде вполне воспроизводимых сигналов, амплитуда которых, впрочем, настолько мала, что их невозможно опознать. Принцип метода выделения чрезвычайно прост, поскольку он заключается в нахождении среднего арифметического значения амплитуд ответов начиная с момента предъявления каждого стимула, так что совпадающие по фазе сигналы ответа складываются, в то время как случайные компоненты фонового шума имеют прогрессирующую тенденцию к нулевому среднему значению. Действительно, подсчитано, что отношение амплитуды искомого сигнала к амплитуде фонового шума растет как √N, где N - число стимулов. Этот метод в настоящее время пользуется большим успехом в электрофизиологии для обнаружения вызванных потенциалов (рис. 10).

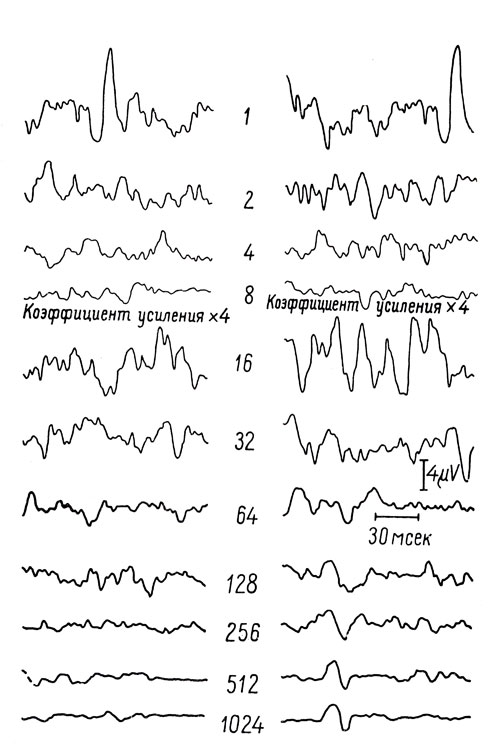
Pис. 10. Обнаружение сигнала, скрытого в фоновом шуме электроэпцефалограммы. Серия звуковых сигналов предъявлялась с частотой 5 в секунду Ответы регистрировались на уровне височных отделов коры. Результаты последовательного сложения 2, 4 ..., 1024 полученных ответов представлены в правой части рисунка (сложение начиналось всякий раз в момент предъявления стимула), в левой части рисунка представлены результаты сложения, начинавшегося независимо от момента предъявления стимула. В последнем случае наблюдается постепенное уплощение кривой в результате случайного распределения положительных и отрицательных потенциалов. Напротив, на правых кривых наблюдается постепенное выявление волны, хронологически связанной со стимулом, предъявление которого служит началом вычислительных операций; латентный период равняется приблизительно 30 мсек. Продолжая увеличивать число сложений, можно улучшить отношение амплитуды обнаруженного сигнала к амплитуде фонового шума на величину, равную корню квадратному из числа сложений. После восьмого сложения коэффициент усиления был умножен на 4, после чего амплитуде кривой соответствует калибровка в 4 м (по Гайслеру)

Точность анализа на практике все-таки подвержена влиянию различных факторов, таких, как нестабильность обнаруженного сигнала (что бывает часто) или независимость составляющих фонового шума (если период стимуляции слишком короткий) .

Можно рекомендовать определение для каждой точки средней величины, характеризующей форму обнаруженного сигнала, пределы достоверности его латентного периода и амплитуды (что до сих пор делается очень редко).