Эффективность экстраполяции времени встречи динамических объектов при различной асимметрии скорости их движения (М. М. Швец)

При решении оператором пространственно-временных задач типа многомерного слежения, требующих от него одновременного наблюдения за несколькими движущимися объектами, эффективность управляющих действий, как известно, зависит не только от числа объектов наблюдения, но также от их динамических характеристик: абсолютной и относительной скорости движения, абсолютного и относительного направления и пространственного расположения объектов в поле зрения оператора. Вместе с тем обширный класс задач указанного типа, где различные траектории движущихся объектов периодически пересекаются в определенные моменты времени, регистрируемые оператором, связан, очевидно, с экстраполирующим поведением, человека, т. е. со способностью более или менее успешно предвосхищать своими действиями развитие наблюдаемого процесса. Причем эффективность экстраполяции при решении таких задач также, по-видимому, зависит от перечисленных выше характеристик динамических объектов.

Для выяснения некоторых элементарных форм этой зависимости была использована одна из простейших экспериментальных моделей названного класса задач. Число движущихся точечных объектов в избранной модели равнялось двум; обе точки двигались равномерно и прямолинейно по горизонтали фронтальной плоскости наблюдения навстречу друг другу (одна - слева направо, другая - справа налево) до момента совмещения (встречи). Независимыми контролируемыми переменными являлись абсолютная и относительная скорость и время движения объектов, а следовательно их относительное пространственное расположение в поле зрения и местоположение точки встречи (совмещения) на заданной траектории. Основной зависимой переменной, измеряемой в эксперименте, было время экстраполирующей реакции человека на момент совмещения объектов (т. е. ошибка рассогласования между временем встречи объектов и временем реакции на момент встречи).

Методически эксперимент строился следующим образом. На горизонтальной светящейся шкале экрана длиной 400 мм, расположенной в 50 см от глаз испытуемого, одновременно и на равном расстоянии от середины шкалы (в 160 мм слева и справа) появлялись два неподвижных темных точечных объекта, которые по истечении 2с с момента появления начинали двигаться навстречу друг другу с различной абсолютной и относительной скоростью. Через 8 с после начала движения точки встречались в разных местах шкалы, исчезая одновременно в момент совмещения.

Таким образом, оба объекта вместе пробегали за время экспозиции одной задачи (10 с) 320 мм шкалы с постоянной во всех задачах суммарной скоростью сближения |V_л| + |V_п| = 40 мм/с.

Отношение их скоростей (|V_л|/|V_п|) принимало следующие 9 значений: 0/40; 8/32; 13,3/26,6; 17,1/22,9; 20/20; 22,9/17,1; 26,6/ 13,3; 32/8; 40/0. Так что коэффициент асимметрии задач по скорости движения объектов A_SV = |V_л| - |V_п|/|V_л| + |V_п| принимал также 9 различных значений: -1, -3/5, -1/3, -1/7, 0, 1/7, 1/3, 3/5, 1.

Задачи с различной асимметрией по скорости движения объектов предъявлялись испытуемым в случайном порядке с интервалом 2 с от окончания экспозиции одной до предъявления следующей задачи. От испытуемого требовалось как можно точнее регистрировать нажатием ключа момент совмещения объектов в каждой задаче. В экспериментах участвовало 10 испытуемых в возрасте от 22 до 35 лет с нормальным зрением. Каждый испытуемый в первой (предварительной) серии экспериментов отрабатывал все 9 задач по 10 раз. Таким образом, для каждой задачи было получено по 100 замеров времени экстраполирующей реакции (t_э).

Статистически обработанные данные первой серии экспериментов показали (рис. 1), что систематическая ошибка экстра-полирующей реакции (Δt_э) уменьшается приблизительно линейно с ростом левой асимметрии задач по скорости от 120 мс при A_SV (лев) = -1 до 40 мс при A_SV (лев) = 1. Это значит, что момент встречи (совмещения) в данных задачах экстраполируется наиболее эффективно при максимальной левосторонней асимметрии по скорости движения объектов и наименее эффективно - при максимальной правосторонней асимметрии.

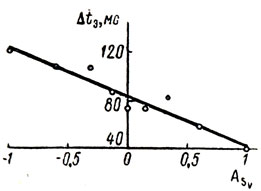
Рис. 1. Зависимость систематической ошибки времени экстраполирующей реакции от асимметрии движущихся объектов по скорости в первой серии экспериментов

Однако при анализе данных первой серии экспериментов возник вопрос, является ли полученная зависимость действительно результатом изменения относительной скорости движения объектов, или решающую роль в эффективности играет просто местоположение точки встречи (совмещения) объектов в поле зрения испытуемого, поскольку это местоположение также изменяется в данных экспериментальных условиях от крайних левой и правой точек рабочей части шкалы до ее середины (т. е. во втором случае систематическая ошибка экстраполирующей реакции может рассматриваться как функция расстояния точки встречи объектов от центра поля зрения, или как функция состояния объектов в момент реакции).

Чтобы выяснить это, было произведено усреднение систематической ошибки экстраполирующей реакции по равноудаленным от середины шкалы точкам встречи объектов. Полученная зависимость изображена на рис. 2. При этом оказалось, что различия ошибки реакции по расстоянию точки встречи объектов от середины шкалы намного ниже различий того же показателя по асимметрии скорости объектов. Кроме того, минимальная ошибка реакции соответствует крайним и средней точкам шкалы, а максимальная ошибка - точкам, расположенным между серединой и краями шкалы. Это позволило предполагать, что решающую роль в эффективности экстраполирующей реакции при данных условиях играет прежде всего динамическая асимметрия объектов (отношение их скоростей), а не положение точки их встречи в центрально-периферическом поле зрения.

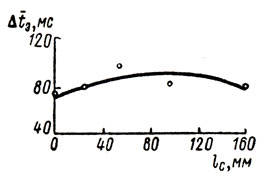
Рис. 2. Систематическая ошибка времени экстраполирующей реакции как функция расстояния места встречи объектов от середины шкалы в первой серии экспериментов

Однако с целью более тщательного исследования зависимости времени экстраполирующей реакции от двух указанных переменных (динамической и статической) была проведена вторая серия экспериментов на той же выборке испытуемых с некоторой модификацией экспериментальной программы. В этой серии ранее решавшиеся задачи, требовавшие от испытуемого лишь регистрации момента встречи объектов, равновероятно и случайно чередовались в программе с задачами, где при тех же начальных условиях (отношении скоростей) и той же конечной реакции (в момент встречи объектов) от испытуемого требовалось дополнительно обнаружить и зарегистрировать нажатием того же ключа случайную помеху на пути движения одного из объектов. Эта помеха имитировалась мгновенным исчезновением правого или левого движущегося объекта через 3 с с момента начала их движения. Причем через 0,5 с после исчезновения объект снова появлялся в соответствующей прошедшему времени точке своей траектории и продолжал движение до момента встречи. Помеха имитировалась в каждом из 9 вариантов задач первой серии, как справа, так и слева, с равной вероятностью. Таким образом, программа второй серии содержала 18 вариантов помех, различавшихся удаленностью места их появления от середины шкалы и лево- или правосторонним положением на шкале.

В этой серии, кроме времени экстраполирующей реакции на момент встречи объектов, регистрировалось число пропусков и обнаружений помех для каждой задачи по каждому из движущихся объектов.

На основании этого определялась эмпирическая вероятность обнаружения мгновенного изменения каждого движущегося объекта во всех задачах, или вероятность обнаружения в различных частях шкалы, что в свою очередь, как предполагалось, могло выявить структуру зрительного поведения в процессе решения данных задач (эффективность контролирования различных зон шкалы).

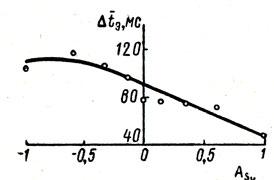
Рис. 3. Зависимость систематической ошибки времени экстраполирующей реакции от асимметрии движущихся объектов по скорости во второй серии экспериментов

Данные этой серии экспериментов удовлетворительно подтвердили полученную в первой серии зависимость систематической ошибки экстраполирующей реакции от асимметрии движущихся объектов по скорости их движения (рис. 3), хотя кривая этой зависимости обнаружила здесь менее линейный характер в области минимальной левосторонней асимметрии скоростей. Зависимость ошибки реакции от местоположения точки встречи объектов на шкале также сохранила ранее обнаруженную тенденцию (рис. 4). Однако различия ошибки по расстоянию точки встречи объектов от середины шкалы проявились в этой серии еще меньше.

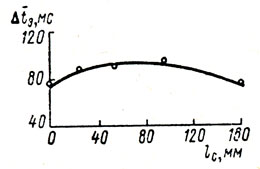
Рис. 4. Систематическая ошибка времени экстраполирующей реакции как функция расстояния места встречи объектов от середины шкалы во второй серии экспериментов

Анализ эмпирической вероятности обнаружения мгновенного изменения движущегося объекта в каждой задаче показал, что эта вероятность нелинейно уменьшается с увеличением расстояния точки появления помехи от середины шкалы (рис. 5). При этом средняя вероятность обнаружения мгновенного изменения объектов слева оказалась в 1,2 раза больше вероятности обнаружения справа, и максимальная вероятность обнаружения соответствует также левой части шкалы (т. е. вероятность мгновенного обнаружения изменения движущегося объекта также имеет в рассматриваемых задачах явно выраженную левостороннюю асимметрию).

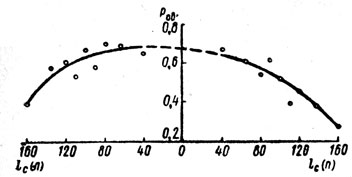
Рис. 5. Зависимость эмпирической вероятности обнаружения мгновенного изменения движущегося объекта от местоположения помехи относительно середины шкалы (влево и вправо) во второй серии экспериментов

Данный факт, очевидно, свидетельствует о том, что левая часть шкалы контролируется в процессе решения задач наиболее эффективно. В силу этого, казалось бы, экстраполирующая реакция на момент встречи объектов в левой части шкалы, т. е. в задачах с минимальной левосторонней асимметрией по скорости, также должна быть наиболее успешной. Однако экспериментальные данные выявили совершенно противоположную картину (рис. 1,3). Следовательно само по себе местоположение точки встречи объектов в поле зрения испытуемого, т. е. статическая характеристика задачи, не играет, по-видимому, решающей роли в эффективности экстраполирующей реакции на момент встречи.

Вместе с тем анализ вероятностной структуры обнаружения мгновенного изменения движущихся объектов в задачах с различной асимметрией по скорости (динамической асимметрией) выявил, что с уменьшением левосторонней асимметрии вероятности обнаружения правого и левого объектов все более уравниваются, хотя вероятность обнаружения каждого объекта в отдельности может расти. А это означает, что с уменьшением левосторонней динамической асимметрии растет эмпирическая средняя неопределенность (энтропия) мгновенного прослеживания каждого из объектов в данных задачах по функции:

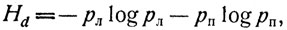
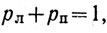
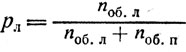
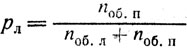
(p_л и p_п - вероятности обнаружения слева и справа в данной задаче; n _об.л и n_oб.п - число обнаружений слева и справа; H_d - средняя энтропия на динамический объект).

Расчет значений эмпирической средней энтропии на динамический объект в рассмотренных задачах показал, что средняя неопределенность динамического объекта растет с уменьшением левосторонней динамической асимметрии примерно потому же закону, что и ошибка экстраполирующей реакции (см. рис. 3, 6). Ранговый коэффициент корреляции значений энтропии и ошибки экстраполирующей реакции равен 0,77. На основании этого можно сделать вывод, поляции момента встречи двух движущихся объектов обусловлена прежде всего их динамическими характеристиками (асимметрией по скорости), которые задают различную меру неопределенности начальных условий решаемой задачи, являющуюся в свою очередь, как известно, ведущим условием успешности экстраполирующего поведения человека.

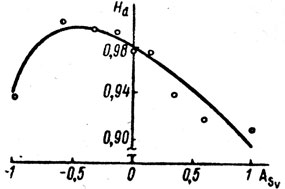
Рис. 6. Зависимость средней эмпирической неопределенности динамического объекта от асимметрии объектов по скорости движения во второй серии экспериментов

Результаты данного экспериментального исследования показали, кроме того, принципиальную возможность эмпирической относительной количественно-информационной оценки динамических задач, т. е. возможность их шкалирования по информационной мере, или мере сложности начальных условий. При этом наиболее простыми для экстраполяции оказались задачи с максимальной левосторонней асимметрией по скорости, которые требуют от человека меньшей информационной загрузки за счет достаточно высоко развитых графических навыков и навыков чтения, имеющих ту же динамическую асимметрию.