Е. А. Умрюхин. Основные направления математической психологии за рубежом

В США, Англии, Франции, Польше и других странах растет число публикаций, посвященных математическому моделированию и анализу психологических явлений. За последние годы появилось несколько крупных монографий и сборников работ по математической психологии [2, 10, 11, 16, 22, 24, 27]. Более трехсот статей опубликовано начиная с 1964 г. в "Журнале математической психологии", издаваемом в США. Периодические издания, посвященные этой теме, выходят и в других странах.

Математические методы, используемые в этих работах, становятся инструментом психологического исследования. Применение математики позволяет конкретизировать формулировки психологических закономерностей, проверять гипотезы" о сущности психологических явлений путем количественного сопоставления следствий из этих гипотез с экспериментальными результатами, получать количественные предсказания результатов психологических процессов при активном воздействии на них с целью их оптимизации.

Подробный анализ современного состояния работ в области математической психологии требует освещения многих аспектов этих работ, таких, как сфера применения математических методов, решаемые проблемы, практические достижения, особенности применяемого математического аппарата и ряд других. В кратком обзоре невозможно подробно рассмотреть все эти вопросы, поэтому главное внимание будет уделено лишь некоторым из них: исторической перспективе развития зарубежной математической психологии, соотношению различных тем в работах, особенностям конкретных задач, решаемых в последнее время. Последний вопрос будет проиллюстрирован примерами.

Рассматривая развитие работ по математической психологии в историческом плане следует в какой-то степени отличать их от работ по применению математики для обработки результатов психологических исследований. В этом отношении есть некоторая аналогия с другими областями науки. Признаны, например, как разные, хотя и пересекающиеся до некоторой степени, такие области науки, как химическая физика и физическая химия, отличают психофизиологию и физиологическую психологию [28]. Разница между этими науками, хотя на первый взгляд и тонкая, но все же вполне ощутимая. Так, химическая физика - это физика, изучающая физические явления, обусловливающие химические процессы, а физическая химия - это химия, пользующаяся для исследования химических явлений физическими методами. Точно так же математическая психология - это психология, использующая математику в качестве инструмента исследования, а психологической математикой можно было бы назвать области математики, которые стимулируются психологическими задачами и используются в анализе и обработке психологических результатов. Сюда можно отнести такие разделы математической статистики, как факторный анализ, дисперсионный, дискрименантный, кластерный анализ и другие подобные математические методы. Известно, что основополагающие работы в этих областях математической статистики, которые сейчас широко используются в самых различных науках, были сделаны за последние 50 лет либо психологами, либо математиками, занимающимися психологическими проблемами.

Математическая психология значительно более молода, чем психологическая математика. Если работы по факторному анализу начали интенсивно развиваться с начала нашего столетия (Ч. Спирмэн, К. Пирсон), то развитие работ по математической психологии началось с конца 50-х годов (Эстес [14], Буш и Мостеллер [5, 6, 7], Эдварде [12, 13], Рестл [26]). Единичные работы появлялись, правда, и раньше (Тэрстоун [30]), Эттлингер [15], Гулликсен [17]). Одной из первых была работа, сделанная нашим соотечественником Н. А. Романовым [1], в которой он предложил математическую модель условного рефлекса.

Интенсивное развитие математической психологии началось с работ, посвященных моделям обучения [5, 14], обнаружения и различения сигналов [6, 26, 29], выбора и принятия решений [12]. Развитию этих работ способствовал прогресс психологии и математики, практические потребности инженерной психологии, появление теории информации, кибернетики, развитие теории управления, применение ЭВМ, сложных систем управления и обнаружения.

Основной отличительной чертой работ в области математической психологии, выделяющих их среди работ по применению математики для обработки психологических результатов, было и является то, что в этих работах, формулировались в той или иной форме модели психологических явлений и закономерностей.

Степень соответствия модели существующему словесному описанию, с одной стороны, и реальности - с другой была разной для первых моделей и для последующих, но существенно, что увеличение этого соответствия было главной целью при разработках моделей.

Можно также отметить, что на первых этапах развития создавались модели, удовлетворяющие имеющемуся словесному описанию психологических явлений при сохранении той степени математической простоты, которая позволяла получить строгие и нетривиальные математические следствия. Такая постановка характерна, например, для первых работ по математическим моделям обучаемости [7].

Однако впоследствии на первый план все больше выступала вторая цель - соответствие модели реальному явлению. Происходит это за счет того, что усложняющаяся по мере своего развития модель по сложности своей концепции начинает удовлетворять самого строгого судью - психолога. После этого модель превращается из средства описания в инструмент непосредственного психологического исследования. Гипотезы о сущности психологических механизмов формулируются в виде конкретных предположений о значениях и связях параметров, включаемых в модель, и условия эксперимента определяются требованием проверки этих гипотез. В последнее время появляется все больше работ, в которых математические модели применяются именно таким образом [20, 23, 32]. Особенно это характерно для исследований в области моделирования обучения памяти. В некоторых работах делаются попытки связать представления о параметрах моделей с физиологическими механизмами, обеспечивающими психические процессы [4]. Один из конкретных примеров такой работы будет приведен ниже.

Печатным органом, наиболее полно представляющим работы по математической психологии за рубежом, является "Журнал математической психологии" (ЖМП), издаваемый в США. Для того чтобы более конкретно представить распределение усилий исследователей, публикующих свои работы в этом журнале, нами была проведена классификация работ, опубликованных в нем с начала его выхода, т. е. с 1964 г., и построено распределение работ по выделенным темам. Для учета динамики развития за эти годы данные были сгруппированы по трехлетним периодам 1964-1967 гг., 1968-1970 гг., 1971-1973 гг. (рис. 1). В основу классификации работ были положены основные направления развития математической психологии. Это соответствует выделению психологических проблем. Действительно, исследователи, из года в год печатающие статьи в ЖМП, посвящают свои работы какой-либо одной психологической проблеме, математические же методы применяются разные, в соответствии с развитием вопроса. Отдельные работы, посвященные развитию математического аппарата, всегда непосредственно связаны с возникающими исследовательскими задачами.

Из рис. 1 видно, что наибольший процент составляют работы по исследованию обучения и памяти. В этой области исследований основное внимание уделяется изучению динамики усвоения (постепенное усвоение или по закону: все или ничего), механизмам кратковременной и долговременной памяти, механизмам забывания, интерференции, переноса навыка, образованию и динамике следов памяти. Наиболее интенсивно на эти темы публикуют работы такие исследователи, как Аткинсон, Бернбах, Уикельгрен, Норман Д., Норман Ф., Грино и др.

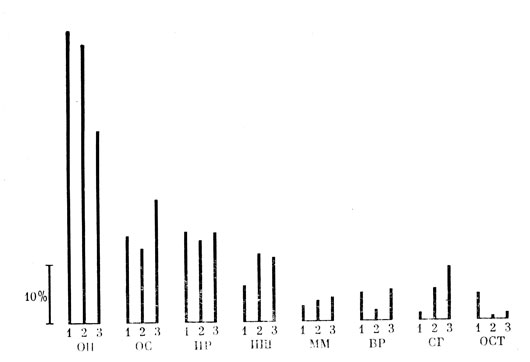
Рис. 1. Распределение в процентах работ, опубликованных в ЖМП по периодам: 1 - 1964-1966 гг.; 2 - 1967-1969 гг.; 3 - 1970 - 1972 гг. Выделены следующие направления работ: ОП - обучение и память; ОС - обнаружение сигналов; ИР - теория игр и принятия решений; ИШ - теория измерений и шкал; ММ - развитие математических методов; ВР - время реакции; СГ - социальное и групповое поведение; ОСТ - остальные темы

В первых работах использовались главным образом математические методы, основанные па применении классической теории вероятности и математической статистики: вычисление моментов распределений, ассимптотических значений величин, описывающих поведение испытуемого. Впоследствии наряду с этим стала широко использоваться теория марковских цепей, определение различных последовательных статистик. Появились также исследования, в которых в качестве средства моделирования используются алгоритмы, реализуемые с помощью вычислительных машин. Модели, построенные этим способом, относятся, пожалуй, к числу наиболее сложных. Примером могут служить модели памяти [18, 21].

Вычислительные машины используются также для проверки соответствия моделей экспериментальным данным и поиска параметров, дающих наилучшее соответствие. Применение ЭВМ особенно актуально в связи с тем, что уравнения, описывающие реальные экспериментальные ситуации, часто получаются слишком сложными для нахождения аналитических решений. Реализуемый с помощью больших ЭВМ метод сеток [3] заключается в том, что вся область допустимых значений параметров разбивается на достаточно малые участки и значения величин, которые служат критериями при сопоставлении с экспериментальными данными, вычисляются на каждом участке. При числе параметров больше трех вычислительная работа чрезвычайно громоздка и ее выполнение возможно только при наличии сверхмощных современных ЭВМ.

Вторую большую группу работ составляют работы по моделированию процессов обнаружения и опознания сигналов, направленные на решение конкретных задач инженерной психологии. Работы эти стимулировались также развитием таких областей математики, как теория принятия решений, теория информации, обнаружения сигналов на фоне помех. Несомненно взаимное влияние психологических и технических исследований в данной области.

Следующая по количественному представительству группа работ посвящена исследованию принятия решения в игровых ситуациях. В этих работах исследуются зависимости субъективных вероятностей исходов и полезностей от объективных вероятностей и ценностей, критерии оптимизации в реальных ситуациях принятия решения, индивидуальные особенности в принятии решения и другие вопросы. Значительные исследования выполнены на эту тему такими авторами, как Эдварде, Тверский и др. В качестве математического аппарата широко используется теория игр, теория автоматов, теория статистических решений, некоторые разделы теории управления.

Как было уже упомянуто выше, в большинстве работ, посвященных специально математическим вопросам, решаются задачи, связанные с конкретными исследованиями. Так, анализируются свойства различных распределений и статистик, применяемых для описания экспериментальных данных, ассимптотические свойства случайных процессов, решаются уравнения, описывающие экспериментальные ситуации. Вместе с тем имеются также работы, посвященные разработке специально математических проблем, которые связаны с описанием сложных психологических явлений. К таким работам можно отнести исследования метрики субъективных пространств, построение шкал, исследования графов, анализ размерностей и др. В указанном направлении работают такие авторы, как Фишбурн, Ганна, Осборн и др.

Для того чтобы посмотреть, проявляются ли какие-либо тенденции развития математической психологии в распределении работ по темам, это распределение, как уже было сказано, определялось по трехлетним периодам.

Из рис. 1 видно, что в последнем периоде (1971-1973 гг.) уменьшается доля работ, посвященных обучению и памяти, увеличивается же число исследований, связанных с инженерной психологией (ОС) и изучением социального и группового поведения (СГ). Это является отражением тенденции к увеличению числа прикладных работ, а также к усложнению моделей и за счет этого анализу более сложных явлений и процессов.

Для иллюстрации специфических особенностей решаемых проблем и применяемых методов ниже приводится более подробное изложение содержания нескольких работ, представляющих разные области исследования.

Первая из этих работ [31] посвящена исследованию принятия решения в ситуации риска. Исходным положением работы является теоретическая концепция о выделении двух главных факторов, определяющих принятие решения: полезности исходов и риска. С помощью математической модели исследуется возможность практического использования этих понятий в конкретной экспериментальной ситуации, решается вопрос о том, можно ли считать эти факторы независимыми.

Автор исходит из предположения, что объективные ценности V предметов преобразуются в субъективные полезности U, а объективные вероятности исходов р в субъективные вероятности s. Ставятся вопросы: каким образом связаны субъективные полезности U с объективными ценностями V, а также субъективные вероятности s с объективными p? Можно ли представить правило принятия решения как выбор альтернативы, для которой ∑U_is_i максимальна (i - номер исхода). Можно ли считать, что U и s независимы?

Автор разработал экспериментальную ситуацию, где в качестве испытуемых выбраны заключенные, с тем чтобы предлагаемые им для выбора объекты: (конфеты и сигареты) имели существенную субъективную ценность. Каждый испытуемый участвовал в экспериментах 4-х серий. В экспериментах испытуемым предлагалась возможность назначить определенную цену за демонстрируемое количество конфет или сигарет. Специальные меры принимались для того, чтобы назначаемая цена соответствовала действительному выбору.

В первой серии экспериментов испытуемым предлагалось назначить цены за разные количества конфет, во второй - за сигареты, в третьей - за сигареты или конфеты без риска, в четвертой серии испытуемому предлагались для оценивания разные количества конфет или сигарет с определенными вероятностями их получения. О значениях вероятностей испытуемый явно информировался. Испытуемый каждый раз должен был назначить ту наибольшую цену, за которую он согласен принять предложенное ему количество сигарет или конфет или участвовать в игре, в которой заданы вероятности исходов. Анализ полученных данных проводился с помощью моделей/ Было рассмотрено 5 моделей. Общим для всех пяти было предположение о выборе той альтернативы, для которой ∑Us максимально. В первой модели (EV) предполагалось U=V,s=р. Во второй модели (SEV) - U=V, s=f (р). В третьей модели (SEU) U=f₁(V), s=f₂ (р), кроме того: a) U не зависит от наличия риска и б) ∑s=1. В четвертой модели (Мх) было снято ограничение а), в пятой (М₂) ограничение б).

Таким образом, третья модель (SEU) является выражением предположения о некоторой трансформации объективных ценностей и вероятностей в субъективные, а четвертая и пятая - проверяют применимость понятий о полезности и субъективных вероятностях как некоторых инвариантах по отношению к условиям эксперимента.

Прием, использованный для выяснения справедливости тех или других гипотез, заключался в следующем. Величины, описывающие выбор U_i, s_i, оценивались из первых трех серий экспериментов, исходя из наилучшего соответствия рассчитанных и экспериментальных данных. Затем на основе полученных оценок для U_i и s_i рассчитывается выбор в 4-м эксперименте. Для разных моделей определяются соответствия между рассчитанными и экспериментальными данными, полученными в 4-м эксперименте.

По степени этого соответствия модели расположились в следующем порядке: М₂≥М₁≥SEU>SEV>EV. Знак > означает явно лучше, знак ≥ означает лучше для некоторых испытуемых. Данных было достаточно для того, чтобы сравнение можно было провести по каждому испытуемому отдельно. Выводы, которые делает автор, можно процитировать полностью: "После более чем 15-ти лет экспериментальных исследований принятия решения в ситуации риска данные в пользу описательной ценности модели SEU остаются сомнительными. Принимая во внимание, с одной стороны, крайнюю обобщенность модели и, с другой - экспериментальные ограничения, можно заключить, что вопрос о том, нужно ли отбросить модель полностью или полностью принять, не является главным. На самом деле основной проблемой является вскрытие того, какие из предположений модели оказываются верными или неверными в различных экспериментальных условиях. В представленном исследовании модель хорошо описывает отдельно случаи выбора без риска и с риском, однако, когда и те, и другие объединяются в одном описании, модель расходится с экспериментом. Таким образом, хотя полезность и субъективные вероятности аддитивны, и субъективные вероятности не зависят от типа выбираемых предметов, полезность не остается инвариантной по отношению к наличию или отсутствию риска. Однако ценность теории полезности для психологии определяется не столько точностью ее предсказания, сколько ее значением, как общей теоретической схемы для изучения индивидуального поведения в условиях выбора".

Из приведенной цитаты видно, что в данном случае математическая модель является инструментом чисто психологического исследования. Являются ли понятия субъективной вероятности и субъективной полезности адекватными при описании процесса принятия решения? Модель позволяет уточнить этот вопрос, показать в какой степени и в каких условиях эти понятия описывают реальный психологический процесс.

Как уже упоминалось, большое число работ посвящено изучению памяти. Главными вопросами, занимающими авторов этих работ, являются вопросы о существовании кратковременной и долговременной памяти, их объеме, механизмах переноса информации из кратковременной памяти в долговременную, механизмах забывания. Гипотезы о формах памяти получают в моделях конкретную интерпретацию, а сравнение теоретических результатов, полученных на моделях, с экспериментальными данными позволяет, с одной стороны, проверить содержательную формулировку гипотезы (например, существует ли промежуточная форма памяти), и, с другой стороны, для принятой гипотезы найти конкретные параметры механизма (например, объем, временпйе характеристики).

Примером такого типа работ является статья Калфи и Аткинсона [8]. Первый вопрос, на который авторы ищут ответ: существенно ли для объяснения процесса запоминания предположение о промежуточном состоянии памяти? Нельзя ли объяснить (т. е. воспроизвести на модели) результаты экспериментов без такого предположения?

Второй вопрос относится уже к выбранной конкретной модели, включающей представление о промежуточной форме памяти: влияет ли на скорость забывания усвоенного материала заучивание нового?

На первый взгляд, постановка подобных вопросов может показаться излишней. Действительно, большинством психологов принимается, без сомнения, существование кратковременной памяти с ограниченным объемом, а также существование ретроактивной интерференции, обусловливающей забывание старого материала при заучивании нового. Что же тогда исследовать?

Однако специфика работ, основанных на применении математических моделей, заключается в том, что они позволяют не только установить, какая из гипотез более верна, но и оценить количественно степень вероятности той или иной гипотезы.

В работе [8] построена трехэлементная модель памяти, являющаяся развитием более ранних моделей одно-и двухэлементных, опубликованных в [2].

Моделируемая ситуация включает эксперименты по заучиванию человеком парных сочетаний, слогов, букв, цифр.

В трехэлементной модели предполагается наличие трех состояний памяти в процессе усвоения парных сочетаний: первое - начальное состояние U, в котором правильный ответ может быть дан только случайно, второе состояние S - промежуточное или кратковременное запоминание - в этом состоянии возможно забывание сочетания с вероятностью f, вероятность правильного ответа в этом состоянии равна единице, если сочетание не забыто. Третье состояние L - состояние долговременного прочного запоминания, в котором всегда дается правильный ответ и забывания нет. Параметрами модели являются величины: с - вероятность запоминания пары, т. е. перехода в S при ее предъявлении, а - вероятность включения пары в долговременную память и f - вероятность забывания в состоянии S.

По числу несвязанных параметров я, с, f модель называется трехэлементной. Заучивание пар описывается с помощью марковского процесса, для которого могут быть вычислены определенные статистики, которые затем сравниваются с полученными в эксперименте.

Эксперимент заключался в предъявлении испытуемому для заучивания пар типа Q - R, где Q - две цифры, а R - одно из сочетаний RIX, FUB, GED. Пары предъявлялись в виде списков, включающих для разных групп испытуемых 9, 15 и 21 пару. Каждый список предъявлялся 10 раз без перерыва.

Для каждой пары учитывались ошибка или правильный ответ. Дальнейшая обработка данных определялась возможностью подсчета для модели определенных величин, в частности, частот сочетаний правильных ответов и ошибок для четырех последовательных предъявлений - 2-го, 3-го, 4-го и 5-го, а также 6-го, 7-го, 8-го и 9-го. Так, например, подсчитывалось, сколько раз встречалось сочетание ОППО, где О - ошибка, П - правильный ответ. Подсчитывалась частота подобных сочетаний для упомянутых последовательных предъявлений пар в эксперименте. Эти же величины определялись для разных моделей. Поскольку число различных сочетаний ошибок и правильных ответов в двух последовательностях из 4-х предъявлений значительно превышало число неизвестных параметров, подбор параметров осуществлялся по минимуму отклонения рассчитанных величин от экспериментальных, оцениваемого с помощью х2. Для нахождения минимума использовался уже упомянутый метод сеток. Разное в разных моделях число несвязанных параметров учитывалось числом степеней свободы.

Из полученных значений χ² видно, что линейная модель не согласуется с экспериментальными данными. Значение χ² далеко выходит за доверительную границу р< 0,001. Для модели "все или ничего" с одним параметром согласие с экспериментальными данными лучше, однако X² также выходит за границу p<0,001. Допустимое согласие получается для рассмотренной трех-эле-ментной модели LS-3 и для модели, которая является видоизменением LS-3, включающим предположение о зависимости вероятности забывания определенной пары от числа промежуточных предъявлений с момента запоминания этой пары до ее воспроизведения.

Таким образом, на поставленные в исследовании вопросы получен следующий ответ. Предположение о промежуточной форме запоминания является существенным для объяснения экспериментальных данных. Что же касается влияния на процесс запоминания промежуточных предъявлений, то хотя учет этого фактора и улучшает соответствие модели экспериментальным данным, по-видимому, в описанном эксперименте влияние этого фактора незначительно.

Еще одна работа [32] приведена для иллюстрации способа проверки соответствия модели описываемым явлениям, основанного на смысловой интерпретации параметров модели. Работа [32] посвящена исследованию динамики следа памяти.

При формулировании основных уравнений, описывающих образование и изменение следа памяти во времени, принимаются во внимание представления, основанные на физиологических механизмах памяти. Из основных аксиом, в которых учитываются консолидация следа во времени и влияние интерферирующей деятельности, получается уравнение l=λехр (-φ√t), где l - сила следа, λ - начальная сила следа при его образовании, ψ - скорость распада следа, пропорциональная степени сходства между заученным материалом и интерферирующим, t - время.

Для проверки модели проводятся эксперименты с вариациями условий, которые, исходя из предполагаемого смысла параметров, должны обусловливать их предсказуемые изменения.

Испытуемым предлагаются для заучивания цифры, причем варьируется время одного предъявления - 3,5 сек. в одном эксперименте и 7 сек. в другом.

Кроме того, после предъявления цифр в качестве интерферирующей деятельности испытуемому предлагается запоминать либо слова, либо наборы из шести символов, три из которых буквы и три - цифры. Предполагается, что начальное усвоение, при времени предъявления 7 сек, будет выше, чем при 3,5 сек. Предполагается также, что скорость распада следа будет выше в случае интерферирующей деятельности второго типа, т. е. при запоминании наборов символов, включающих цифры.

Подбор параметров модели осуществляется исходя из наилучшего соответствия предсказываемых результатов экспериментальным данным.

Оказывается, что получающиеся при этом значения параметров хорошо согласуются с предполагаемым их смыслом - значение ψ - увеличивается примерно в два раза для второго типа интерферирующей деятельности и зависит главным образом от нее, λ - уменьшается при уменьшении времени предъявления.

Приведенная работа иллюстрирует намечающуюся тенденцию применения моделей для интерпретации физиологических механизмов, обеспечивающих психические процессы. Следует заметить, что как рассмотренные работы, так и большинство работ, публикуемых в ЖМП, характеризуют скорее промежуточные этапы исследования проблем, чем законченные разработки.

Однако развитие работ идет чрезвычайно быстро. Модели усложняются, описывают все более широкий класс экспериментальных условий. Появляются также работы, направленные на решение практических вопросов. Важной областью практического применения математической психологии является инженерная психология. Другой проблемой является оптимизация обучения, усвоения нового материала. Имеется несколько работ, в которых на основе уравнений рассматриваются оптимальные стратегии обучения [9, 19], пока только в экспериментальных условиях.

Общее современное состояние исследований хорошо представлено в сборнике [22], в котором опубликованы обобщающие работы наиболее известных авторов, занимающихся математическим описанием обучения и памяти.

В плане дальнейшего развития этих работ характерна статья [25], в которой автор обращает внимание на необходимость отказа от многих упрощений, принятых в созданных моделях. В частности, утверждается, что память нельзя отрывать от целенаправленной познавательной деятельности, что в моделях необходимо учитывать активное отношение испытуемого к экспериментальной ситуации, его целевую установку, мотивы деятельности и т. д. Интересно, что к этим предпосылкам, которые близки к фундаментальному положению нашей отечественной психологии о необходимости рассмотрения всех психических явлений в аспекте целенаправленной деятельности, зарубежные авторы приходят, отталкиваясь от математического моделирования анализируемых психических явлений.

Резюмируя, можно отметить следующее. Математическая психология вторгается в самые разные области исследования: от простых условных рефлексов до социальных явлений. Однако в каждой области пока выбираются только такие ситуации, в которых есть возможность ограничить число переменных, описывающих процесс, и установить простые функциональные связи между ними. Поэтому фактическая область применения методов математической психологии пока сравнительно узкая. Однако результаты такого проникновения оказываются полезными. С помощью математических моделей удается в ряде случаев проверять различные гипотезы о психологических механизмах исследуемых процессов.

Главными задачами, которые ставят в настоящее время исследователи в области математической психологии, являются следующие: усложнение моделей за счет более глубокого отражения в них сущности психических процессов, учета качественной их стороны; создание для этого адекватного математического аппарата; уточнение условий, при которых оказывается справедливым то или иное предположение, проверяемое с помощью моделей.

В заключение хотелось бы в нескольких словах обрисовать перспективу развития математической психологии. Возможно, что сказанное ниже может показаться до некоторой степени фантазией. Однако можно напомнить начало развития математики и механики. Со времени появления дифференциального счисления до "открытия на кончике пера" новой планеты прошло около 200 лет. В настоящее время математическое описание психологических явлений находится на начальной стадии. Но темпы развития науки стали другие. И не исключено, что уже через 10-20 лет станут возможными открытия на "кончике пера" в психологии. Для завершения аналогии с развитием математики, механики, физики остается напомнить другое крупное событие в этой области. Принципиальная возможность расщепления атомного ядра с выделением огромных количеств энергии была определена теоретически более чем за 10 лет до практического осуществления. Овладение атомной энергией явилось одним из крупнейших достижений физики в управлении силами природы и предпосылкой к этому было создание теоретических моделей, уравнений, позволяющих получать варианты решений при различных условиях.

Психология стремится дать человеку средства управления психическими процессами. Не исключено, что именно математическая психология приведет к решающему сдвигу в этом направлении.