2. Теоретико-информационная модель деятельности оператора

Наиболее общее суждение о работоспособности операторов в рамках теоретико-информационного подхода может быть получено путем сравнения информации, которую оператор должен переработать на фиксированном отрезке времени для достижения конечной цели управления, и той информации, которую он фактически способен переработать за это время в конкретных условиях деятельности.

Оценки количества информации, которую оператор должен переработать в тех или иных условиях, будут рассмотрены в последующих параграфах настоящей работы.

Основной задачей данного параграфа является разработка такой модели деятельности оператора, которая позволяла бы получить оценки для фактически перерабатываемой им информации. При этом мы ограничимся здесь случаем простейшей структуры деятельности оператора, построенной на принципе априори предусмотренной реакции на каждый из сигналов из заранее известного алфавита.

Мы будем рассматривать один из самых важных для практики случаев, когда человека-оператора можно представить как стохастический блок в целостной системе контроля и управления. Задачей этого блока является выработка сигналов управления, т. е. построение специального взаимооднозначного отображения множества внешних сигналов, несущих информацию о состояниях объекта управления (L_x), на множество управляющих воздействий (L_у).

Главное, что отличает рассматриваемую структуру от других состоит в том, что множество различимых для оператора состояний информационной модели и множество различимых для объекта управляющих воздействий находятся во взаимнооднозначном соответствии. Другими словами, эта структура характерна тем, что любое различимое состояние информационной модели несет в себе всю необходимую и достаточную информацию для формирования соответствующего управляющего воздействия оператора.

В соответствии с принятыми исходными положениями приемлемая для практического использования математическая модель должна обеспечить: а) возможность оценки числа ЭО, реализуемых оператором на интересующем нас отрезке времени; б) оценку информативности каждого ЭО.

Предполагая использовать для этих целей указанную выше модель дискретного канала связи с дискретным временем, определим характеристики входного (L_x) и выходного (L_у) пространств событий канала.

По определению под пространством входных событий канала будем понимать множество различимых для оператора состояний совокупности индикаторов, индикационных устройств, размещенных на информационной модели системы.

Пусть n - общее число индикаторов рассматриваемой панели и q_i i=1, 2, ... n - число различимых для оператора состояний i-го индикатора. Тогда, используя известные теоремы комбинаторики, легко показать, что общее число различимых состояний такой многоэлементной панели дается формулой:

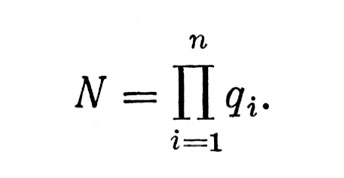
Обозначим через x_j (j=1, 2, ... N) произвольный j-й элемент входного пространства L_х канала или, что все равно, j-е различимое состояние информационной панели системы.

По аналогии с предыдущими рассуждениями под пространством выходных событий канала L_у, по определению, будем понимать множество различимых для объекта состояний совокупности органов управления, предусмотренных конструкцией пультов управления. Выше уже отмечалось, что в целесообразно спроектированной системе управления пространства L_х и L_у эквивалентны по числу элементов. Поэтому мы перенумеруем элементы пространства выходных событий L_у так, чтобы элемент у_j соответствовал тому управляющему воздействию операторов, которое должно быть реализовано при состоянии информационной панели X_j.

Для характеристики функционирования канала во времени введем на интересующем нас отрезке времени 0≤t≤Т такую упорядоченную систему моментов:

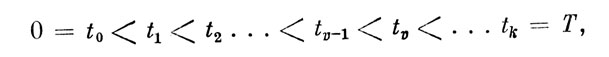
что протяженность произвольного v-ro ЭО оператора будет составлять величину

Тогда исчерпывающее статистическое описание пространства входных событий канала L_х может быть получено, если для любого j=1, 2, ..., N задать безусловные вероятности Р (хj;ν) реализации элемента x_j на отрезке времени соответствующему ν-му ЭО оператора в порядке следования ЭО с момента t=0.

По условию нормировки для любого произвольного ν-гo ЭО указанные выше безусловные вероятности реализации элемента x_j - из L_х удовлетворяют соотношению:

Для дальнейшего рассмотрения удобно трактовать вероятности Р (x_j;ν) как ν-проекции N-мерного вероятностного вектора различимых состояний информационной панели:

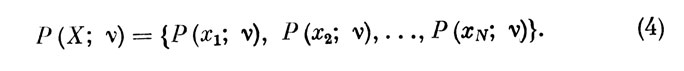
Пусть, далее, значения Р (yfiv) характеризуют безусловные вероятности реализации у_j-гo управляющего воздействия оператора на интервале времени, соответствующем ν-му ЭО.

Тогда :

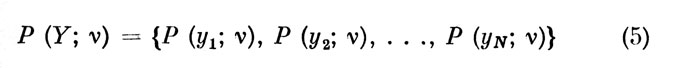
также можно рассматривать как N-мерный вероятностный вектор различимых управляющих воздействий оператора, соответствующих ν-му ЭО.

Опираясь на все предыдущие рассуждения в рамках рассматриваемой структуры процессов, мы можем выразить математическую модель деятельности оператора следующей формулой:

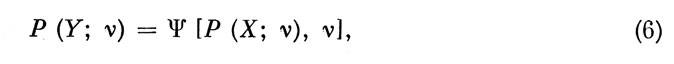
где ψ - символ в общем случае нестационарного преобразования дискретной последовательности различимых состояний информационной панели (элементов пространства L_x) в дискретную последовательность различимых для объекта управляющих воздействий оператора (элементов пространства L_у). Физический смысл этого преобразования достаточно очевиден. Действительно, как мы видели выше, по смыслу задачи, решаемой оператором в рамках рассматриваемой структуры деятельности и при отсутствии ошибок в формировании и реализации управляющего воздействия, оператор должен в ответ на каждое х_j-e состояние информационной панели с вероятностью единица реализовать соответствующее ему заданное управляющее воздействие у_j. Легко видеть, что в этом частном случае (6) принимает вид:

где M₁ - единичная матрица размерности N Х N.

В условиях реальной деятельности приходится считаться с наличием разного рода ошибок оператора, как некоторого звена управляющей системы. В терминах предлагаемой модели оператора появление указанных ошибок следует объяснять наличием ненулевых внутренних шумов канала связи. В силу этого при любом входном событии из L_x сохраняется ненулевая вероятность реализации любого из управляющих воздействий, предусмотренных конструкцией пульта управления системы, т. е. любого элемента пространства L_у.

Используя формулы полной вероятности для безусловной вероятности Р (у_j; ν) реализации у_j-гo управляющего воздействия на дискретном интервале времени, соответствующем ν-му ЭО оператора, можно написать:

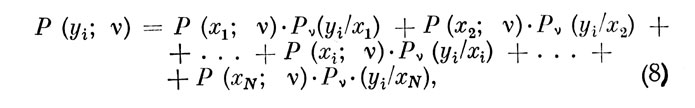
где i=1, 2, .., N, а индекс ν в условных вероятностях Pν(у_j/x_i) подчеркивает свойство нестационарности используемой математической модели канала, в силу которого указанные условные вероятности являются функциями порядкового номера эффективности отсчета, начиная с момента t=0.

На основе этой функциональной зависимости от номера ЭО представляется возможным учесть такие специфические характеристики оператора, как адаптация к ситуации, врабатываемость и утомляемость, способность к совершенствованию деятельности в процессе обучения и т.д.

Используя соотношение (8), выписанное для всех i=1, 2, .., N, нетрудно заметить, что в этом общем случае (6) приводится к виду:

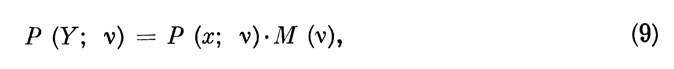
где М (ν) - матрица условных вероятностей размерности N X N. Структура этой матрицы имеет вид

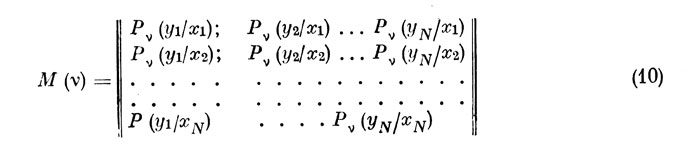
Матрица М (ν) из (10) удовлетворяет всем признакам стохастической матрицы, поскольку все ее элементы неотрицательны, не превосходят единицы и сумма элементов каждой строки равна единице. Эта матрица является специфической для каждого оператора в том смысле, что отражает его индивидуальные характеристики, связанные с приемом и переработкой информации в рамках рассматриваемой структуры деятельности. Более того, можно сказать, что эта матрица в свернутом виде отражает процессы подготовки, принятия и реализации решения на сенсорно-перцептивном уровне при решении задачи установления соответствия заданного типа между L_х и L_у. He менее важно и то, что она учитывает и весь комплекс условий предъявления и полезного использования информации. Конечно, лишь в той мере, в какой эти условия влияют на ошибочные действия оператора.

Отсутствие содержательных психологических моделей функционирования оператора в задачах такого типа не позволяет на данном этапе использовать аналитические методы расчета элементов матрицы М (ν). Однако в любом конкретном случае деятельности оператора матрица М (ν) без каких-либо принципиальных затруднений может быть получена экспериментально.

Попутно, в процессе указанных экспериментов выявляются и все имеющиеся недостатки в формировании информационной панели и пульта управления, а также появляется возможность сравнивать между собой различных реальных операторов и оценивать их близость к "идеальному".

Мы будем, в соответствии с логикой предыдущего изложения, считать, что "идеальный оператор" реализует заданное однозначное и безошибочное отображение входных сигналов - элементов из L_x на множество выходных управляющих воздействий - элементов из L_у. Тогда объективное суждение о недостатках конструкции системы и оценку функционирования реального оператора можно получить на основе сравнения экспериментально полученных матриц М (ν) с единичной матрицей той же размерности, отвечающей случаю идеального функционирования оператора.

Полученные выше математические модели деятельности операторов (7) и (9) вместе с матрицей (10) могут быть непосредственно использованы для оценки степени фактической информационной нагрузки реальных операторов.

Рассмотрим в этих целях произвольный ν-ный ЭО на отрезке времени функционирования оператора. Пусть хμ - состояние информационной панели, отвечающее этому отсчету. При формировании реакции на это состояние оператор, в силу наличия внутренних шумов, может допустить ошибку и ввести в объект любое из управляющих воздействий у_j, j= 1, 2, ..., N, предусмотренных конструкцией пульта управления. Распределение вероятностей этих воздействий в рамках используемой математической модели дается μ-oй строкой матрицы М (ν). Совокупность условных вероятностей этой строки матрицы определяет частную условную энтропию управляющих реакций оператора при фиксированном входном сигнале:

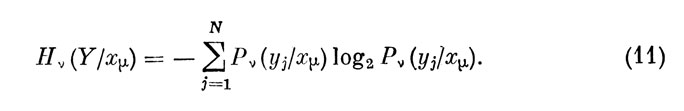
Если эту энтропию усреднить по всем возможным состояниям информационной панели на ν-м дискретном интервале с учетом вероятностей их реализации, то получим общую условную энтропию:

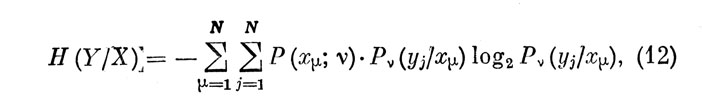
характеризующую среднюю неопределенность управляющих реакций оператора под действием внутренних шумов на ν-ом интервале.

Естественно, что при идеальном функционировании оператора частная и общая условные энтропии из (11) и (12) равны нулю, так как элементы любой строки матрицы М (ν), кроме диагональных, равны 0, а диагональные элементы равны 1.

Для определения информативности ν-гo ЭО, т. е. количества информации, которое оператор фактически перерабатывает на соответствующем отрезке времени, воспользуемся известной в теории информации формулой средней взаимной информации I_ν (У, X) между элементами входного и выходного пространств канала в виде:

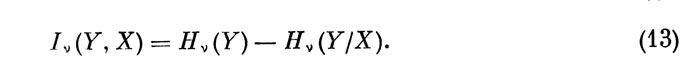
По определению энтропия H_ν (У) из (13) формируется на основе составляющих вектора Р (У, ν) в виде:

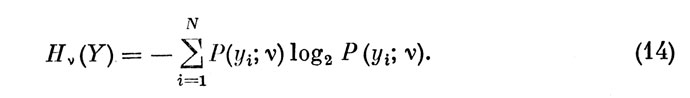
В свою очередь, вероятности Р (у_i, ν) находятся из соотношения (9), отражающего общий случай функционирования оператора.

Подставляя (12) и (14) в (13), получаем выражение для оценки количества информации, перерабатываемой оператором в течение ν-гo ЭО:

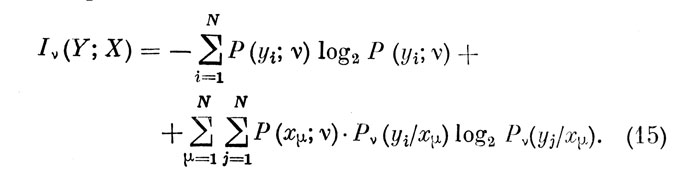
Из (15) легко видеть, что в случае безошибочного функционирования оператора на v-ом интервале количество обрабатываемой им информации равно:

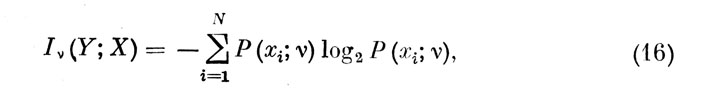
т. е. численно совпадает с энтропией различимых состояний информационной панели на отрезке времени, соответствующему ν-му ЭО.

Соотношения (15) и (16) позволяют непосредственно перейти к распространению теоретико-информационной модели деятельности оператора на конечные отрезки времени, охватывающие некоторую последовательность ЭО. Очевидно, что для этих целей приведенные выше соотношения должны быть дополнены соотношениями, которые характеризуют последовательность работы оператора во времени.

Основные трудности на этом пути обусловлены главным образом стохастическим характером процесса функционирования оператора. Учет этого обстоятельства приводит к необходимости считать временные затраты оператора на реализацию ν-гo отсчета случайными величинами, подчиненными определенным законам распределения. В рамках рассматриваемой структуры деятельности число различных в содержательном смысле ЭО, с которыми оператору приходится иметь дело, совпадает с числом элементов пространства входных событий L_x, т. е. равно N.

Поэтому для описания деятельности оператора во времени достаточно задать N функций распределения вероятностей временных затрат оператора на реализацию рассматриваемой совокупности ЭО.

Если при этом оказывается необходимым учесть еще и преобразование и изменение характеристик работоспособности оператора на отрезке времени функционирования вследствие обучаемости, усталости, под действием стрессоров и т. п., то параметры указанных распределений должны быть специфичными для каждого ν-гo отсчета. Поэтому необходимую исходную информацию для описания функционирования оператора во времени целесообразно представить в виде матричной функции распределения вероятностей

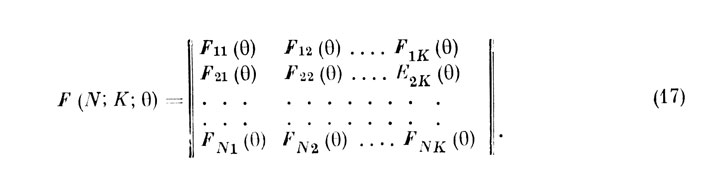
Матрица F (N; К; 6) имеет размерность N X К, причем нумерация строк матрицы совпадает с нумерацией элементов пространства входных событий L_x, а нумерация столбцов соответствует порядковым номерам ЭО, реализуемых оператором с момента t=0. Произвольный элемент Рц (6) матрицы по физическому смыслу представляет собой интегральный закон распределения временных затрат δ_ij на реализацию j-го ЭО, соответствующего элементу х_i пространства входных событий, т. е.:

Наряду с матричным интегральным законом распределения (17) будем далее рассматривать соответствующую ему матричную функцию плотности распределения вероятности:

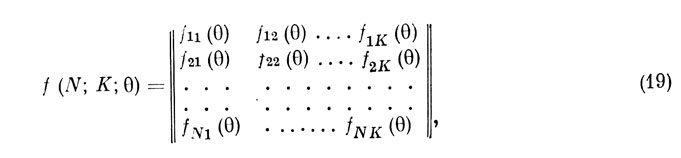
а также матричную характеристическую функцию:

По определению характеристической функции, произвольный элемент φ_μl (λ) матрицы (20) выражается через соответствующий элемент матрицы f (N, К; θ) из (19) следующим образом:

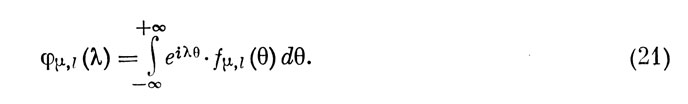
И в этом случае, как и прежде, из-за отсутствия необходимых теоретических данных не представляется возможным на данном этапе произвести аналитические расчеты элементов матриц (17), (19) и (20). Единственно возможный путь их практического определения в настоящее время состоит в сборе, систематизации и обобщении статистических данных по экспериментальным исследованиям деятельности операторов с использованием многоэлементных информационных панелей.

В заключении этого параграфа отметим, что полученные соотношения (15) и (16), рассматриваемые в совокупности с матрицами (17), (19) и (20) представляют собой все необходимые элементы информационного описания функционирования оператора в рамках рассматриваемой структуры деятельности и позволяют перейти к оценкам количества информации, перерабатываемой оператором па конечных отрезках времени.