3. Количественные оценки информационной загрузки оператора

(В настоящей работе основное внимание уделено определению количества информации, фактически перерабатываемой оператором. Вопросы, связанные с определением количества информации, необходимой и достаточной для управления с заданной точностью комплексом объектов, рассматриваются в [1, 5, 8]; а методы непосредственного определения количества информации, предъявляемой на информационной модели, - в работе [7], развивающей идеи [4])

Задачей настоящего параграфа является объективная оценка информационной загрузки операторов в системах контроля и управления различными реальными объектами. Объективные количественные оценки фактической информационной напряженности операторов являются необходимой исходной базой для оценки и прогнозирования характеристик работоспособности реальных операторов и качества их функционирования в системах контроля и управления. Они необходимы также для определения оптимальной структуры самой управляющей системы на основе решения задачи оптимального распределения функций, для выбора оптимальной структуры информационных панелей и пультов управления, для разработки оптимальных алгоритмов деятельности операторов в тех или иных конкретных условиях и т. д.

В общем решении этой проблемы целесообразно выделить некоторые типовые частные' случаи, различающиеся по принципам исследования, по необходимым исходным данным и конечным результатам.

Все многообразие возникающих здесь задач естественным образом разбивается на два больших класса. Первый класс охватывает задачи апостериорного информационного анализа уже свершившейся деятельности оператора и преследуют цели выявления его фактической информационной загрузки, которая привела к тем или иным результатам.

Второй класс задач связан с проблемой синтеза будущей деятельности оператора и имеет конечной целью прогнозирование того уровня информационной загрузки, которую оператор может фактически реализовать в тех или иных условиях. Задачи прогнозирования информационной загрузки операторов в условиях будущей деятельности являются, несомненно, гораздо более сложными и специфичными но сравнению с задачами анализа. Исследования показывают, что второй класс задач в связи с этим целесообразно также разбить на подклассы, различающиеся спецификой функционирования объектов контроля и управления. В частности, специального рассмотрения заслуживают задачи прогнозирования загрузки операторов в тех случаях, когда управляемые объекты работают по жесткой временной или по жесткой логической программам. Естественно, что такие программы, в известной мере, детерминируют деятельность операторов и в связи с этим изменяют общий уровень его информационной загрузки. Очевидно также, что оба эти подкласса задач существенно отличаются от общего случая стохастического функционирования объекта управления, когда оператор лишен какой-либо детерминированности в схеме развития процесса и во времени, и в пространстве входных событий. В качестве примера рассмотрим две из указанных задач.

Апостериорные оценки информационной напряженности оператора в системе контроля и управления

Апостериорные оценки фактической информационной напряженности операторов имеют большое практическое значение во всех тех случаях, когда приходится анализировать их деятельность для выявления причин, приведших к срыву в работе или к каким-либо другим нежелательным последствиям.

В качестве необходимых исходных данных для такого анализа на основе введенной выше информационной модели оператора необходимо иметь:

- хронометраж прошедшей деятельности оператора, позволяющий, в частности, определить общее число реализованных им ЭО, а также привязку каждого из них к оси времени;

- данные об ошибочных действиях оператора, позволяющие определить как общее число ошибок, так и распределение на рассматриваемом отрезке времени функционирования;

- статистические характеристики объекта управления в той мере, в какой это необходимо для получения вероятностного вектора Р (X; v) его различимых состояний для любого v-ro отсчета из множества отсчетов, реализованных оператором.

Пусть мы имеем Ω (Т) - множество ЭО, фактически реализованных оператором на отрезке времени 0≤t≤Т, и ω (Т) ∈ Ω (Т) - подмножество безошибочно реализованных отсчетов. Тогда количественная оценка информации с учетом (16) может быть представлена в виде:

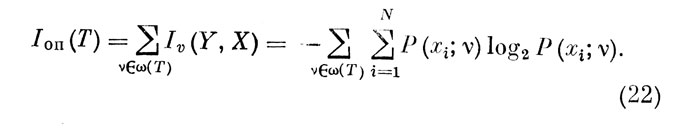
Количество информации, потерянное оператором на том же отрезке времени (под влиянием внутренних шумов канала):

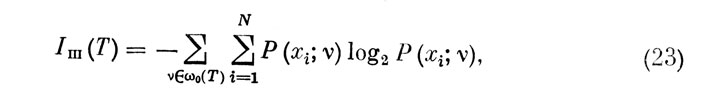
где ω₀(Т)=[Ω(Т) - w(T)] - подмножество ошибочных ЭО операторов.

Объективную оценку качества функционирования оператора на отрезке времени О≤t≤Т можно построить путем сравнения его с "идеальным оператором", т. е. сопоставив количество информации, фактически переработанное оператором по (22), с тем, которое он должен был переработать для достижения конечной цели контроля и управления. При этом можно выяснить, являются ли допущенные оператором срывы в работе следствием его информационной перегрузки (сопоставив полученные результаты с имеющимися данными о предельной пропускной способности оператора). Попутно при таком же анализе находятся те интервалы времени, на отрезке 0≤t≤Т, которые являются наиболее напряженными в информационном отношении, а также те состояния информационной панели, которые представляют наибольшие трудности для оператора при приеме и переработке входной информации.

Следует заметить, однако, что в общем случае информация, фактически перерабатываемая оператором па конечном интервале времени, может отличаться от необходимой и достаточной не только за счет потерь, прямо обусловленных его ошибочными реакциями. Более существенными в ряде случаев могут оказаться потери, связанные с недостаточным быстродействием оператора, когда фактически реализованное им количество ЭО оказывается значительно меньше необходимого. (Оценки необходимого числа ЭО рассматриваются далее). Это обстоятельство также необходимо учитывать при оценке качества деятельности реального оператора и всей системы контроля и управления в целом.

Прогнозирование уровня информационной загрузки оператора в системах с объектами, функционирующими по жесткой временной программе

Специфика рассматриваемого класса задач обусловлена тем, что контролируемые процессы объекта детерминированы во временной области. Любая программа такого рода определяется заданием на отрезке 0≤t≤Т некоторой упорядоченной последовательности фиксированных моментов времени 0=t₀<t₁<..._k=Т, которые соответствуют программным переходам объекта из одного различимого состояния в другое. Стохастичпость программы в этих условиях порождается тем, что для любого из указанных выше моментов времени может сохраняться ненулевая вероятность перехода объекта в любое из N различимых состояний, где N определяется по формуле (1). Каждый момент t_i в рамках рассматриваемого подхода естественно отождествлять с моментом начала соответствующего ЭО. В свою очередь, интервалы времени Δ_ν=t_ν-t_ν-1 между соседними переходами определяют время, которым оператор располагает для реализации ν-гo отсчета, а сумма ∑^k_ν=1Δ_ν характеризует отрезок времени, на котором рассматривается деятельность оператора.

При прогнозировании информационной загрузки оператора в данном случае целесообразно выделить два этапа. Первый из них естественным образом связывается с прогнозированием числа ЭО, которое оператор способен реализовать на отрезке 0≤t≤Т. При этом условимся считать ν-й отсчет нереализованным, если за отводимое время Δ_ν оператор не смог обработать предъявляемую информацию и сформировать ответную реакцию. В противном случае ν-й отсчет будем считать реализованным. Однако вследствие наличия внутренних шумов оператора эта реализация может быть, в свою очередь, правильной и ошибочной.

Поэтому вторым этапом прогнозирования информационной загрузки будет прогнозирование информативности каждого ν-гo отсчета оператора с учетом прогноза его ошибочных действий.

Таким образом, в качестве исходных данных для решения поставленной задачи необходимо иметь:

- заданную последовательность фиксированных моментов времени t-n i = 1, 2, . . ., К, характеризующую рассматриваемую временную программу функционирования объекта;

- статистические характеристики исследуемого объекта, достаточные для определения вероятностного вектора его различимых состояний Р (X; ν) на любом интервале Δν отрезка 0≤t≤Т;

- обобщенные статистические данные по временным затратам оператора на реализацию ЭО в виде матричной функции F (N; К; θ) из (17);

- обобщенные статистические данные по ошибочным действиям оператора при работе с рассматриваемой информационной панелью в виде матрицы условных вероятностей М (v) из (10).

Тогда, используя принятые ранее обозначения, условие реализуемости произвольного v-ro ЭО в указанном выше смысле можно представить в виде:

δ_ν≤Δ_ν для всех ν= 1, 2, ..., К.

Пусть А_ν - случайное событие, отвечающее выполнению этого условия. Найдем его вероятность. Из предыдущего ясно, что условные вероятности Р [Aν/(x_i;ν)], характеризующие реализуемость ν-гo отсчета, при условии, что на отрезке Δ_ν объект может находиться в любом из N различных состояний, даются ν-м столбцом матрицы F (N; К; θ) из (17), если во все элементы этого столбца подставить θ=Δν:

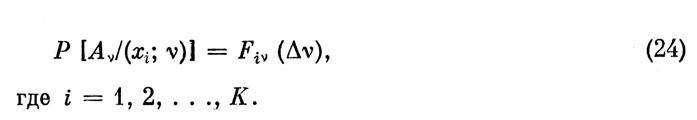
Тогда, используя (4) и формулу полной вероятности, находим безусловную вероятность реализации ν-гo ЭО в виде:

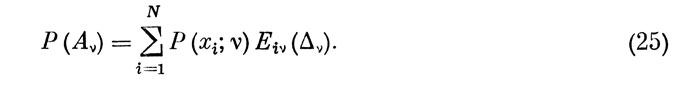
Пусть теперь А_ν - событие, противоположное A_ν. По физическому смыслу А_ν соответствует случаю, когда оператор при реализации ν-гo отсчета не уложился в располагаемое время.

Из (25) вероятность этого события:

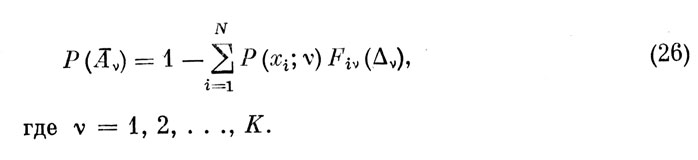
Таким образом, каждый из К ЭО, предусматриваемых рассматриваемой программой, может быть реализован оператором с вероятностью Р (А_ν) и не реализован с вероятностью Р (A_ν). В силу этого общее число вариантов реализации программы равно:

Ф(К)=2^К. (27)

Для оценки вероятности каждого варианта, а также для последующего перехода к оценке количества информации, которое оператор фактически перерабатывает в рамках того или иного варианта, важно знать, какой именно из последовательных ЭО будет реализован оператором, а какой нет. С этой целью введем специальную систему кодирования ЭО и вариантов реализации программы. Пусть gν, ν=1, 2, ..., К - "вес" ν-гo ЭО определяется соотношением:

и пусть G_в.п. - "вес" варианта реализации программы, причем

Из (28) и (29) легко видеть,, что GB.U. принимает целочисленные значения на отрезке 0≤G_в.п.≤2^К-1. Поэтому значения G_в.п. из указанного промежутка вполне могут быть отождествлены с порядковыми номерами вариантов реализации программы оператором.

Так, например, значению G_в.п.=0 соответствует случай, когда оператор не смог реализовать ни одного ЭО из предусмотренных программой. Значению G_в.п.=1 соответствует случай, когда реализован лишь первый ЭО и т. д.

Основное достоинство введенного способа кодирования выявляется в результате представления любого G_в.п. из указанного выше промежутка в двоичной системе счисления. Действительно, двоичное выражение G_в.п. содержит К двоичных разрядов, причем номера разрядов справо налево совпадают с порядковыми номерами ЭО. Значащие цифры каждого разряда в соответствии с (28) и (29) указывают, реализован соответствующий ЭО или нет. Поскольку в рамках модели канала без памяти последовательные ЭО статистически независимы, то вероятность того или иного варианта реализации программы Р (G_в.п.) выражается произведением К сомножителей типа Р (Аν) или Р (Aν) в зависимости от того, содержат ли ν-й разряд двоичного выражения G_в.п. в качестве значащей цифры единицу или нуль. В соответствии с этим, например,

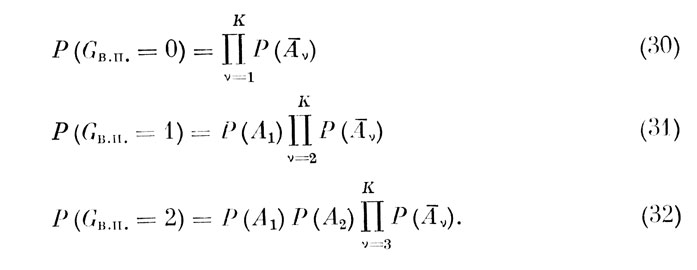
Для получения оценок количества информации, фактически перерабатываемой оператором при различных вариантах реализации программы, введем в рассмотрение систему из Ф (К) множеств со (G_в.п.). Элементами каждого из множеств со (G_в.п.) являются порядковые номера ЭО, реализуемых оператором в рамках данного G_в.п. -го варианта программы, или порядковые номера разрядов в двоичных выражениях GH.n., содержащих единицы в качестве значащих цифр.

Искомая оценка фактически перерабатываемой оператором информации по G_в.п.-му варианту реализации программы на основании (15) может быть представлена в виде:

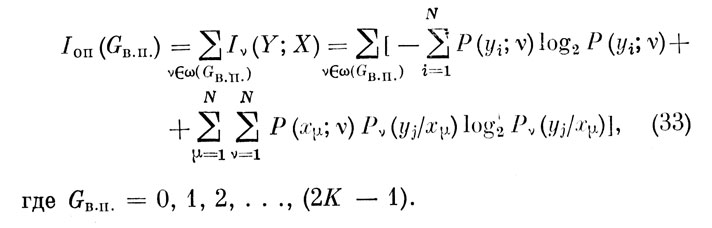
Таким образом, количество информации, которое фактически перерабатывается оператором в рамках любой программы из класса программ, детерминированных во времени, оказывается дискретной случайной величиной. Значения этой величины определяются соотношением (33) при различных значениях бв.п.. Вероятности реализации этих величин однозначно связаны с вероятностями вариантов реализации программы и определяются соотношениями типа (30 - 32), выписанными для соответствующих G_в.п.. Варианты реализации программы оператором несовместны и составляют полную группу событий, поскольку нетрудно показать, что:

Действительно, справедливость равенства (34) для К=1 очевидна, так как в этом случае программой предусматривается лишь один эффективный отсчет оператора. В принципе возможны лишь два варианта выполнения программы, когда этот отсчет реализуется оператором и когда не реализуется. Левая часть (33) содержит всего два слагаемых, которые в сумме дают единицу как вероятности противоположных событий.

Пусть теперь (33) справедливо для некоторого К=m, т. е.:

Используя индукцию по К, покажем, что (34') справедливо и для К=m+1.

Для доказательства заметим, что в силу (27) увеличение числа ЭО в программе на единицу приводит к увеличению числа вариантов реализации программы в два раза. При этом каждый вариант продолжается на (m+1)-й отсчет двояким образом, в зависимости от того, реализуется он оператором или нет. Учитывая это обстоятельство, разобьем множество вариантов реализации программы из (m+1) отсчетов на два подмножества:

Ф(m+1)=Ф₁(m+1)+Ф₂(m+1). (35)

Условимся считать, что подмножество Ф₁(m+1) содержит лишь те варианты, в которых (m+1)-й отсчет не реализуется оператором. Тогда Ф₂(m+1) содержит все варианты, в которых (m+1)-й отсчет является реализованным. Подмножество Ф₁ и Ф₂ эквивалентны между собой по числу элементов. Следовательно, учитывая процедуру формирования слагаемых в левой части (34), можем написать:

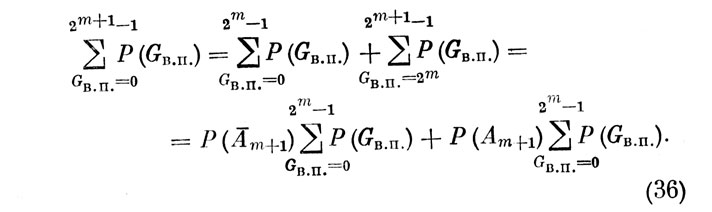
Отсюда, учитывая (34) и тот факт, что события А_m+1 и A_m+1, противоположны, получаем:

что и требовалось доказать.

Варианты реализации любой программы из рассматриваемого класса программ, детерминированных во времени составляют полную группу несовместных событий. Поэтому соотношение (34) совместно с соотношениями (30-33), выписанными для всех 0≤G_в.п.≤2^K-1, определяют дискретный ряд распределения количества информации, перерабатываемой оператором при реализации любой программы из рассматриваемого класса. Интегральная функция распределения случайной величины имеет вид:

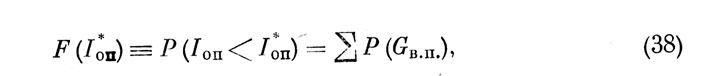
где суммирование ведется по всем G_в.п., удовлетворяющим условию I_оп(G_в.п.)<I_оп

Итак, класс программ, детерминированных во времени, является весьма благоприятным с точки зрения прогнозирования характеристик информационной загрузки операторов. Используя введенное выше аналитическое описание модели канала, для любой программы этого класса, оказывается возможным прогнозировать интегральный закон распределения количества информации, перерабаты ваемой оператором.

В настоящей работе мы рассмотрели апостериорные оценки информационной загрузки оператора и один из конкретных примеров прогноза информационной загрузки оператора в системах, работающих по жесткой временной программе. Другие примеры информационных оценок операторской деятельности в системах контроля и управления детально анализируются О. В. Ронжиным [10].

Здесь нам хотелось подчеркнуть перспективные возможности применения расширенного аппарата теории информации для оценки операторской деятельности в широком классе задач контроля и управления с опорой на исходные психологические данные. Естественное развитие указанного здесь подхода может идти по двум важнейшим направлениям.

Первое из них предполагает дальнейшее развитие и применение метода интегральных информационных оценок с последующим усложнением модели канала связи, включением памяти и последействия в канале. Этот путь дает возможность построить удовлетворительные описания надежности и эффективности работы человека-оператора в реальных системах контроля и управления; он позволяет получать сравнимые описания функционирования "человеческой" и "технической" части всей системы. При наличии достаточно полного эмпирического материала - инженерно-психологических и экспериментально-психологических данных о работе оператора при приеме и переработке сигнальной информации,- изложенный здесь метод дает возможность эффективно прогнозировать реальные информационные загрузки операторов в системах.

Второй путь связан с теоретико-психологическим анализом, экспериментально-психологическим обоснованием и использованием предложенной здесь модели "идеального оператора". Структурный анализ особенностей сенсорно-перцептивных процессов и построение формальных моделей этих процессов дает возможность получать использованные в данной работе матрицы, характеризующие работу оператора, не только эмпирическим, но и расчетным путем. Эта работа требует глубокого анализа собственно психологических особенностей познавательных процессов, поиска методов эффективной и экспрессной оценки важнейших параметров этих процессов и факторов направленного изменения их.

Таким образом, в дайной статье мы наметили один из возможных вариантов синтеза интегральных информационных оценок деятельности человека-оператора с оценками локальных структурных особенностей психических процессов, ответственных за протекание этой деятельности.

В заключение отметим наиболее важные, на наш взгляд, прикладные результаты изложенного подхода.

1. Проведенное исследование показывает возможности использования информационных методов для оценки входной и выходной информации в системах контроля и управления. Непременным условием применения этих методов в психологии является: учет структуры изучаемого процесса; учет качественных характеристик воспринимаемой и перерабатываемой информации; учет временной неопределенности потоков информации. Чем более глубоко будут учтены эти условия, тем более корректно использование принципов и методов теории информации.

2. Предложенный метод может быть использован как для оценки эффективности реально работающего оператора, так и для некоторого прогноза эффективности его деятельности. Кроме того, этот метод можно использовать в качестве предварительной основы для синтеза реальных систем контроля и управления, при оценке временной динамики и особенностей деятельности оператора при работе с реальными информационными моделями в системах контроля и управления, а также для оценки самих информационных моделей с точки зрения эффективности их конструкции для операторов данного класса. Таким образом, можно оцепить степень согласования данной информационной модели с характеристиками информационной способности данного оператора.

3. Наконец, анализ предложенной теоретико-информационной модели позволяет выработать базу для сравнения реальных операторов с идеальным по виду матрицы М (ν) (10) и оценить качество работы, сравнивая их матрицы М (ν) между собой. Таким образом, несмотря на некоторую обобщенность модели, которая отражает интегральные характеристики деятельности оператора, она вполне может быть использована для нормативной оценки как операторов, так и информационных моделей в системах контроля и управления сложными объектами.