2. Формирование функции прогноза

Традиционное решение задачи диагностики или прогноза методами многомерного корреляционного анализа сводится к нахождению уравнения множественной линейной регрессии (УМЛР) вида

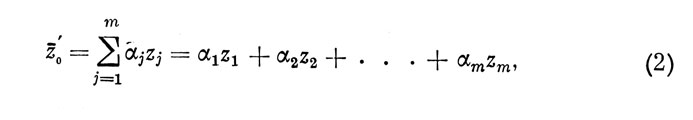
которое позволяет определить среднее ожидаемое (в вероятностном плане) значение оценки z_0i. индивида i по внешнему критерию при данной совокупности значений z_1i z_2i ... z_mi оценок индивида по m признакам (индекс i в формуле (2) опущен). Здесь α₁, α₂, ..., α_m - коэффициенты регрессии, а все индивидуальные оценки выражены в нормированном виде в соответствии с равенством

где x_j и σ_j соответственно обозначают среднее значение и среднеквадратическое отклонение совокупности оценок всех индивидов выборки объемом N по признаку j.

Эффективность УМЛР оценивают по величине коэффициента множественной корреляции (КМК)

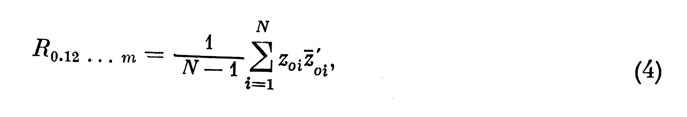
который по смыслу можно определить как коэффициент линейной корреляции между фактическими оценками индивидов z_0i по внешнему критерию и соответствующими им прогнозируемыми значениями z_0i, вычисленными с помощью УМЛР (2).

Обычно стремятся к получению УМЛР, позволяющего оценивать прогнозируемое значение критерия с помощью минимального числа т самых существенных признаков. Такое УМЛР является значительно более устойчивым и удобным для реализации, чем базирующееся на большом числе признаков. Поскольку два любых корреляционно связанных признака заключают в себе некоторую долю общей для них информации, и тем большую, чем выше коэффициент корреляции между ними, то добавление к уже отобранным каждого нового признака вносит все меньший дополнительный вклад в общую эффективность прогноза. Поэтому важное значение для минимизации числа т имеет порядок отбора признаков для их включения в систему УМЛР.

Первый (по значимости) признак легко выделить по наибольшей его корреляции с внешним критерием. Отбор последующих признаков в принципе возможен следующим образом. Поочередно рассматриваются УМЛР, образованные сочетанием первого признака с каждым из остальных, и для всех парных вариантов рассчитывается КМК. Максимальное значение последнего позволяет выявить второй (по значимости) признак. Затем поочередно рассматриваются УМЛР, получаемые при сочетании первых двух отобранных признаков с каждым из оставщихся, и по наибольшей величине КМК находится третий (по значимости) признак и т. д. С каждым новым отобранным признаком прирост КМК будет все меньшим, и когда он становится статистически незначимым отбор можно считать завершенным.

Подобная методика отбора наиболее существенных признаков весьма трудоемка. Значительно проще задача решается методом "просеивания" переменных, предложенным Н. А. Багровым [3] и основанным на последовательном построении матриц частных коэффициентов корреляции после каждого шага отбора признаков для УМЛР.

Суть метода "просеивания" переменных поясним на примере корреляционной матрицы, приведенной в табл. 3, а. В одной половине матрицы записаны условные обозначения коэффициентов корреляции, а в другой - соответствующие им численные значения, полученные на выборке из 78 студентов физкультурного ВУЗа, для конкретного комплекса признаков, которым условно присвоены индексы 0, а, б, в, г и д. Поставим цель сформировать УМЛР, позволяющее прогнозировать успехи студентов в метании копья, исходя из их веса и роста, а также спортивных результатов в спринтерском беге на 100 м, прыжках в высоту и длину.

В столбце "0" матрицы 3,а находим наибольший коэффициент корреляции с критерием, который отвечает признаку (а); присваиваем последнему № 1. Следовательно, r₀₁=0,531. Затем строим новую корреляционную матрицу (табл. 3, б), в которой признак а - 1 исключен, а элементами являются частные коэффициенты корреляции (ЧКК) между остальными признаками, вычисленные из условия исключения влияния признака № 1 по известной формуле

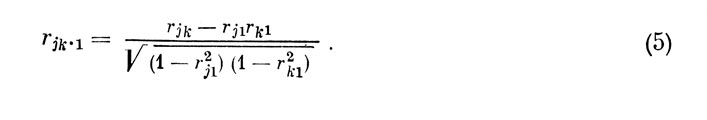
По столбцу "0" этой матрицы определяем признак (г), который имеет наибольший ЧКК с критерием и, следовательно, является вторым по значимости; заменим его индекс на № 2. Тогда r_02•1=0,369. После этого строим следующую корреляционную матрицу (табл. 3, в), в которой исключен и признак № 2, а элементами являются ЧКК,

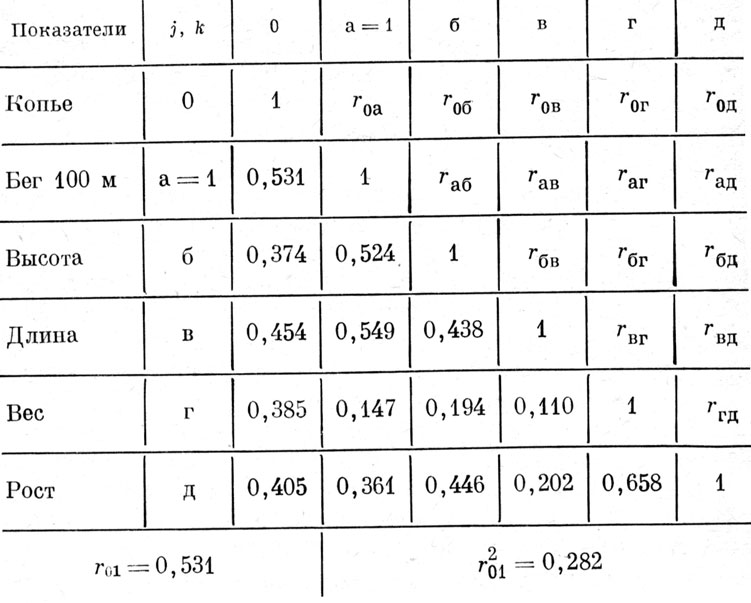
Таблица 3. Корреляционные матрицы. а)

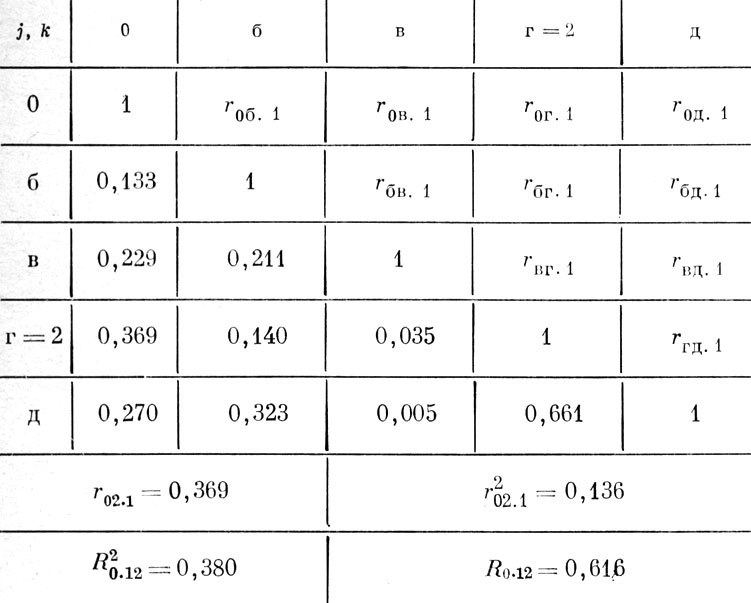
Таблица 3. Корреляционные матрицы. б)

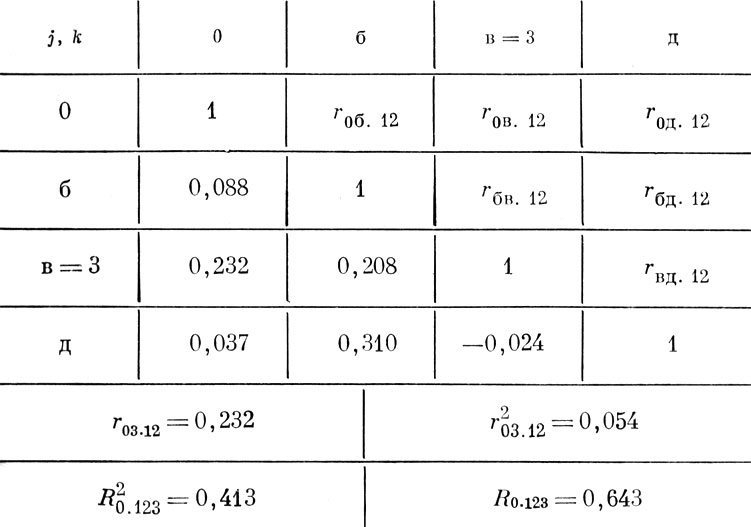
Таблица 3. Корреляционные матрицы. в)

Таблица 3. Корреляционные матрицы. г)

Таблица 3. Корреляционные матрицы. д)

вычисленные из условия исключения влияния признаков № 1 и 2 по формуле

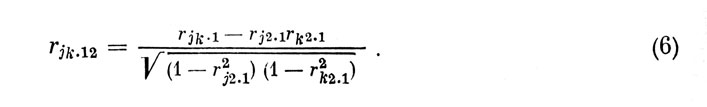
По максимальной величине r_03•12=0,232 находим третий по значимости признак в. Затем аналогичным образом (табл. 3, г, д) находим четвертый (д) и пятый (б) по значимости признаки.

Рассмотренный метод требует проведения однообразных и сравнительно простых вычислений ЧКК. Его трудоемкость прогрессивно возрастает с увеличением числа учитываемых признаков. Но практически не требуется процесс ранжирования признаков по значимости доводить до конца, как мы это делали выше в примере. Если после каждого шага отбора вычислять КМК, то отбор признаков можно прекращать, когда прирост последнего станет незначительным.

Если вычисление КМК производить по известным из математической статистики формулам, как это предполагает Н. А. Багров, то резкое усложнение последних с ростом числа признаков заметно снижает преимущества метода "просеивания". Однако имеется возможность существенно упростить вычисление КМК, используя промежуточные результаты, получаемые в процессе ранжирования признаков по значимости.

Определим зависимость между квадратами смежных значений КМК, разделенных одним шагом ранжирования признаков. После первого шага, когда выделены признаки №. 1 и 2, имеем:

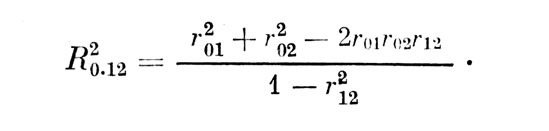
Это выражение можно привести к более простому виду:

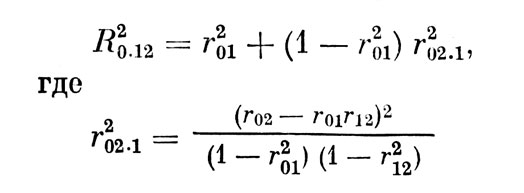
есть квадрат наибольшего ЧКК первого столбца таблицы 3,6. После следующего шага преобразований, приводящего к выделению признака № 3, получаем:

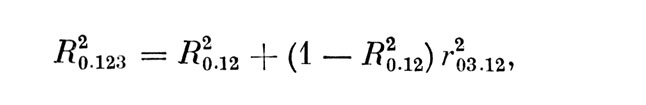
где ЧКК r_03•12 находится из табл. 3, в. В общем случае, при оценке существенности j-го признака

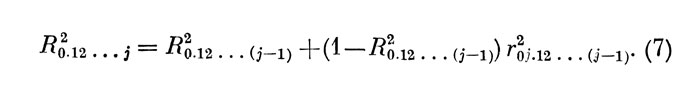
Следовательно, для определения КМ К необходимо знать его значение, предшествующее последнему гаагу преобразований, и ЧКК между критерием и последним оцениваемым признаком при исключении влияния всех ранее отобранных признаков.

Данные вычислений КМК для рассматриваемого примера приведены под соответствующими матрицами табл. 3. Из них видно, что для прогноза средних значений критерия успешности в метании копья наиболее информативными являются оценки по трем признакам: бегу на 100 м и прыжкам в длину испытуемого и его собственному весу, которые в совокупности обеспечивают получение КМК R _0•123=0,643.

В большинстве практических случаев число существенных для УМЛР признаков колеблется в пределах от двух до пяти; это позволяет производить необходимые расчеты по предлагаемой методике, пользуясь лишь простейшими вычислительными средствами.

После окончательного отбора т признаков, для завершения формирования УМЛР (2) остается произвести расчет коэффициентов регрессии α₁ α₂, ..., α_m. Классические формулы расчета, предложенные Г. Крамером [4], при m>3 становятся настолько сложными, что практически требуют применения ЭВМ. Однако, используя данные последовательно получаемых при методе "просеивания" корреляционных матриц, можно предложить более простую методику вычислений.

Ниже приводится (без выводов) сводка расчетных формул (для различных значений m≤5). Расчет во всех случаях начинается с последних значений коэффициентов регрессии, например при m=5 коэффициенты рассчитываются в следующем порядке: α₅, α₄, α₃ α₂ α₁

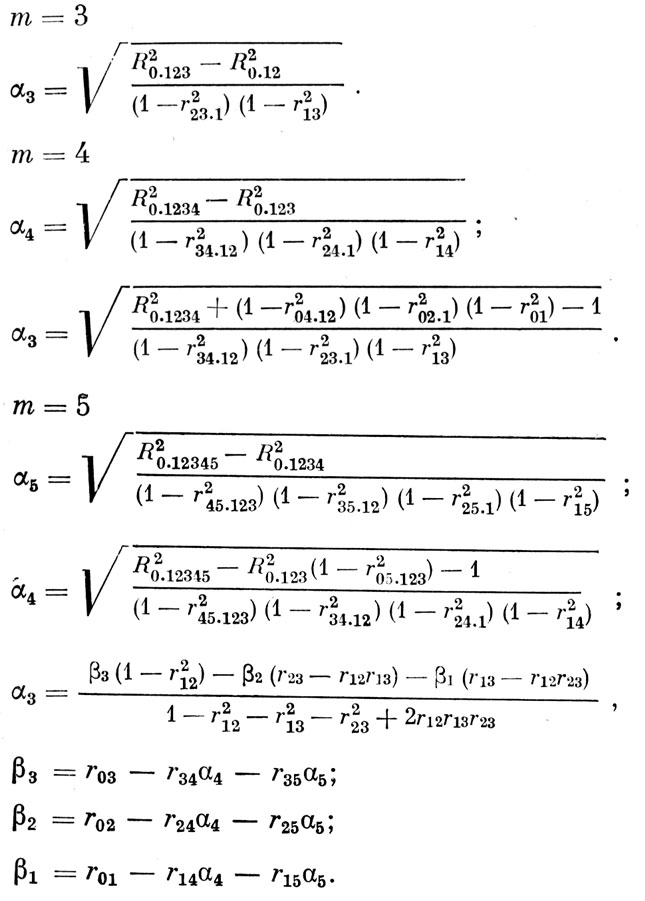
Сводка расчётных формул (для различных значенийm=5)

При любых значениях m коэффициенты α₂ и α₁ находятся по формулам:

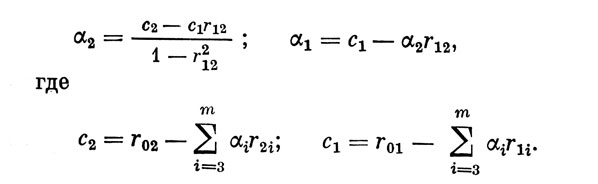
Для численного примера, соответствующего корреляционной матрице табл. 3, а, УМЛР получилось следующее:

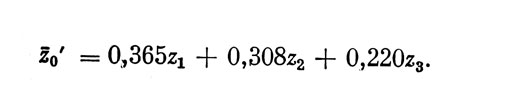
Таким образом, формирование функции прогноза можно свести к следующим действиям: 1) по данным откорректированной корреляционной матрицы методом "просеивания" производится ранжирование признаков по степени их значимости (относительно критерия успешности); 2) в процессе ранжирования признаков после каждого шага определяются КМК; 3) по окончании отбора самых существенных признаков рассчитываются коэффициенты регрессии УМЛР.