1. Корреляция исходных данных

Многомерный корреляционный анализ, как известно, базируется на расширенной корреляционной матрице

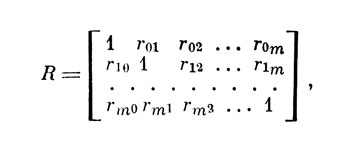
включающей в себя все парные коэффициенты корреляции между (m+1) признаками (переменными, показателями), измеренными у индивидов некоторой представительной выборки. Индекс "0" относится к внешнему критерию (например, профессиональной успешности), подлежащему диагностированию или прогнозированию, остальные индексы - к признакам, которые предположительно (на основе прошлого опыта, литературных данных, теоретических изысканий или интуиции исследователя) могут служить для предвидения оценок по внешнему критерию.

Поскольку реальная значимость каждого признака может быть выявлена лишь в ходе исследования, то первоначальный комплекс признаков берется обычно заведомо избыточным с учетом возможности его последующей коррекции. Само собой разумеется, что для всех выбранных признаков шкалы измерений и условия, в которых осуществляются наблюдения или испытания индивидов выборки, должны обеспечивать получение адекватных результатов.

Строго говоря, правомерность применения корреляционного анализа ограничивается лишь такими комплексами переменных, совокупности оценок которых распределены по нормальному закону, а корреляционная связь между оценками каждой пары переменных носит линейный характер. Данные экспериментальных исследований всегда в большей или меньшей степени отклоняются от указанных требований, и задачей исследователя является оценка допустимости наблюдаемых отклонений для каждого признака. Однако многие исследователи, учитывая трудоемкость проведения соответствующих проверок, попросту их игнорируют и тем самым способствуют отбору некорректных признаков. Но и те исследователи, которые затрачивают большой труд на тщательную проверку закономерностей эмпирических распределений и их сравнение с нормальным (а это требует вычисления коэффициентов асимметрии и эксцесса, критериев согласия и т. д.), а также на проверку линейности всех парных корреляционных связей (посредством вычисления корреляционных отношений и коэффициентов нелинейности), не всегда достигают цели, поскольку им приходится иметь дело с новым огромным массивом цифровых данных, требующим сложного квалифицированного анализа.

Процесс коррекции первоначального комплекса признаков может быть значительно упрощен, если его производить на уровне корреляционной матрицы (1). Прежде всего следует выявить и исключить из комплекса малоинформативные признаки, коэффициенты корреляции которых с внешним критерием малы, например меньше половины от второго по величине значения в первой строке матрицы (1). Затем можно выделить пары взаимно дублирующих признаков, коэффициент корреляции между которыми весьма высок (порядка 0,8 и выше), а по отношению к любому другому признаку - примерно одинаков; один из элементов каждой такой пары подлежит исключению.

С целью выявления целесообразных приемов предварительного анализа и обработки исходных данных для выборки из 258 человек, проверенных по комплексу из 36 психофизиологических и антропометрических признаков, показателей физического развития и критерию успешности, нами были построены полигоны эмпирических распределений оценок и вычислены в трех вариантах корреляционные матрицы: непосредственно по экспериментальным оценкам и оценкам нормализованным, т. е. искусственно приведенным к нормальному закону распределения (коэффициенты корреляции Пирсона), а также по оценкам, преобразованным, в ранговые, т. е. приведенным к равномерному распределению (коэффициенты корреляции рангов). Оказалось, что аналогичные коэффициенты корреляции всех трех вариантов в большинстве случаев имеют близкие численные значения даже при весьма различающихся распределениях эмпирических оценок, часто далеких от нормального закона. Из 630 трех-вариантных значений коэффициентов корреляции лишь в 26 случаях величины последних для различных вариантов заметно различались, причем эти коэффициенты корреляции оказались связанными с одной и той же группой из пяти признаков, распределения оценок которых обладали определенными особенностями.

Обобщение полученных результатов привело нас к заключению, что коэффициенты корреляции мало зависят от характера распределения оценок исследуемых признаков в средней их области, в частности от модальности кривых распределения, при условии, если эти кривые не имеют резко асимметричной формы с максимумом в граничной точке или вблизи нее. Большие ошибки могут создавать граничные оценки, резко отличающиеся численно от основной массы оценок по данному признаку. Эти оценки не обязательно относятся к категории промахов; при объективных физиологических обследованиях и испытании физических свойств нередко приходится сталкиваться с отдельными экстремальными (в масштабе исследуемой выборки) индивидуальными данными или результатами. Если отклонение этих оценок от средних значений в несколько раз превышает среднеквадратичное отклонение или имеется значительное число оценок с большим отклонением, то некоторые коэффициенты корреляции, вычисленные по эмпирическим данным, могут заметно отличаться от значений, получаемых при упорядочении этих данных посредством их ранжирования или нормализации.

При предварительном просмотре экспериментальных данных следует выявлять подобные экстремальные ("выскакивающие") оценки [2]; если они не являются промахами, то не обязательно исключать их из рассмотрения, допустимо изменить их численную величину, приблизив ее к значению ближайшей к ним оценки. При большом числе экстремальных оценок может оказаться рациональной замена экспериментальных оценок ранжированными. Искусственная же нормализация оценок, по нашим наблюдениям, не дает ощутимых преимуществ по сравнению с их ранжированием.

Сравнение аналогичных коэффициентов корреляции, вычисленных соответственно по экспериментальным и ранжированным оценкам, и анализ одномерных и двумерного распределений сопоставляемых признаков приводят к следующим выводам:

1) если указанные коэффициенты корреляции примерно одинаковы, то возможные отклонения в закономерностях распределений и линейности связи данных признаков практически несущественны;

2) если указанные коэффициенты корреляции данного признака заметно различаются между собой и ато имеет место по отношению ко многим признакам исследуемого комплекса, то можно предположить, что этот признак имеет резко аномальное распределение оценок и его следует исключить;

3) если существенное различие указанных коэффициентов корреляции наблюдается лишь по отношению к нескольким признакам комплекса, то можно ожидать, что корреляционная связь с последними у данного признака резко нелинейная. Если нелинейная связь обнаруживается по отношению к внешнему критерию, то признак следует исключить.

Здесь и далее мы рассматриваем лишь принципиальную сторону вопроса и не касаемся конкретных количественных норм оценки существенности различий между аналогичными коэффициентами корреляции, поскольку этот вопрос требует специальных исследований.

Таким образом, если вычислять корреляционную матрицу в двух вариантах, базирующихся соответственно на совокупностях экспериментальных и ранжированных оценок, то сравнение аналогичных коэффициентов корреляции позволит быстро выявить некорректные признаки, заменяя сложный и утомительный анализ закономерностей распределений и парных корреляционных зависимостей. Но ранжирование оценок признаков, особенно при большом числе последних и крупной выборке, хотя и не требует высокой квалификации работника, занимает немалое время, даже при использовании ЭВМ. Поэтому возник вопрос о возможности замены экспериментальных оценок простыми модифицированными, сохраняющими исходную (или обратную ей) иерархию оценок, но пе требующими ранжирования. С целью проверки такой возможности для нескольких комплексов признаков, характеризуемых различными закономерностями распределения оценок, были рассчитаны парные коэффициенты корреляции в 49 вариантах. Им соответствовали следующие семь нелинейных модификаций оценок каждого признака (обозначая экспериментальные оценки через х): х, 1/x, √х, x², 1/x², ln x. При этом были получены результаты, аналогичные случаю использования ранжированных оценок.

Чтобы оценить, хотя бы качественно, мощность предлагаемого метода проверки корректности признаков, приведем два примера.

1. Коэффициенты корреляции между результатами в метании копья (у) и весом испытуемых (х), вычисленные в 49 указанных выше вариантах для выборки из 78 студентов физкультурного ВУЗа (распределения оценок обоих признаков не имеют заметных экстремальных особенностей) (табл. 1).

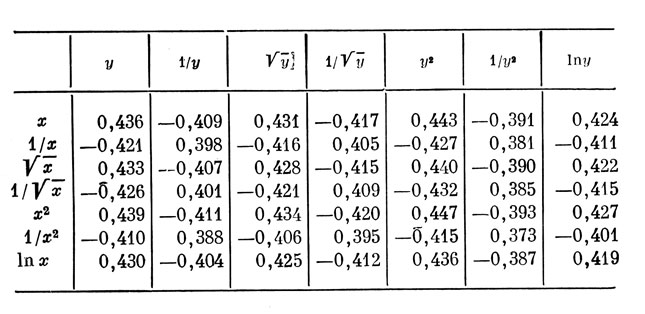
Таблица 1. Коэффициенты корреляции между весом х и результатами у спортсменов

2. Коэффициенты корреляции между ранжированными оценками профессиональной успешности (у) и результатами бега па 400 м (х), вычисленные для выборки из 75 курсантов технического училища (связь между этими оценками резко нелинейная) (табл. 2).

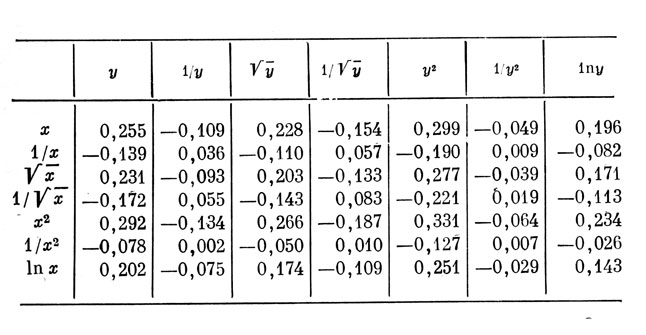
Таблица 2. Коэффициенты корреляции между результатами бега х и оценками профессиональной успешности

Достаточно высокой чувствительностью к аномальностям распределений оценок и линейностей связи обладают коэффициенты корреляции, вычисленные на основе обратных значений экспериментальных оценок (1/у, 1/x), расчет которых не представляет большого труда. Они при проверке корректности признаков вполне могут заменить коэффициенты корреляции, базирующиеся на ранжированных оценках. При этом, конечно, необходимо, чтобы шкалы оценок всех признаков не содержали градаций, равных нулю или близких к нему.

Таким образом, в результате анализа вычисленной в двух вариантах корреляционной матрицы можно избавиться от многих первоначально выбранных малоинформативных, взаимнодублирующих и некорректных признаков, что облегчит дальнейший труд по выработке оптимального решения.