История развития теоретических идей на примере моделей обнаружения сигнала

По нашему убеждению, от центральной модели - обнаружения сигналов, при достаточно простых дополнительных предположениях, можно перейти к описанию сенсорных процессов в задачах, связанных с дифференциальными порогами и с некоторыми абсолютными порогами ощущений. Далее я хотел бы коротко остановиться на общей структуре тех процессов, которые составляют основу психологического материала в описаниях ситуаций обнаружения сигналов. Для этого обратимся к схеме, представленной на рис. 1.

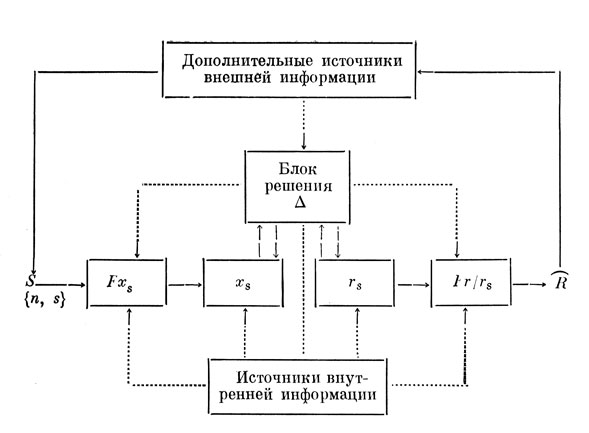
Рис. 1. Схема анализа сенсорно-перцептивных процессов

Существует некоторое ограниченное множество внешних сигналов S, которое тем или иным образом отображается в множество впечатлений или психических образов внешних сигналов - ощущений. Далее, существует некий аппарат или блок решения, который на основании имеющегося сенсорного материала вырабатывает множество возможных ответных реакций или возможные формы поведения. Кроме того, существует источник внутренней информации, и он генерирует ту информацию, которая поступает в работающую систему (сенсорный процесс) через другие психические структуры. И, наконец, существуют источники дополнительной внешней информации.

Естественно, что выходная информация, связанная с результатами ответных реакций, в том или ином виде возвращается на вход работающей системы, образуя (возможно, частично) замкнутый контур циркулирования информации. Понятно, что любые потоки информации, внешние или внутренние, определенным образом детерминируют работу системы и отдельных ее блоков и тем самым влияют на течение сенсорного процесса.

Приведенная схема позволяет грубо оценить состояние моделирования сенсорной системы на психофизическом уровне в настоящее время. Источники внутренней информации объединяют различные системы, связанные с работой мнемических, регуляционных и прогнозирующих механизмов, включая особый мотивационно-оценочный механизм. В различных моделях (мы частично увидим это далее) рассматриваются различные источники внутренней информации, при этом оговариваются некоторые особые свойства их. Под внешней информацией понимается обычная входная информация, которая является результатом потенциальных и реальных изменений состояний внешней среды, в том числе под влиянием ответных реакций самого организма. Конечно, сюда же включается та информация, которая поступает в виде потока специальных сигналов "обратной связи" - в виде непосредственных изменений некоторых состояний внешней среды или в виде информации от учителя (в широком смысле), оценивающего результаты реального или возможного поведения.

В задаче обнаружения сигналов множество состояний среды, определяющее главное содержание психического отражения, т. е. собственно сенсорный материал, составлено из двух основных подмножеств. Первое содержит различные динамические состояния шума, фона и разного рода помех, второе - объединяет различные сигналы, подлежащие обнаружению или выделению из этого фонового окружения. Чаще всего подмножество подлежащих обнаружению сигналов состоит из одного элемента.

Выходное множество ответных поведенческих реакций также может быть разбито на два (или более) подмножества: можно разделять определенные реакции в ответ на наличие сигнала и определенные реакции в ответ на отсутствие сигнала. Чаще всего выходное множество содержит два элемента: например, вербальные реакции "да, сигнал был", "нет, сигнала не было".

Важно отметить, что указанные выше разделения входного и выходного множеств в задачах обнаружения не являются классическими разбиениями: в большинстве практически полезных случаев выделенные подмножества имеют ненулевое пересечение.

Проблема возможного дальнейшего расщепления входного и выходного множеств, т. е. случай, когда подмножества сигнала и подмножества ответных реакций содержат более чем по одному элементу, не представляет принципиального интереса для нас. Она заключается в том, что при этом происходит перераспределение процессов, связанных с организацией и принятием решения, и для качественного анализа нашей задачи не является важной. Поэтому мы остановимся на задаче обнаружения, имеющей самую простую структуру, т. е. когда входное множество содержит один сигнал на фоне шума или его отсутствие, а выходное - составлено из двух допустимых реакций: да - нет.

Мы рассмотрим, как описывают психофизические модели работу сенсорной системы в такой ситуации и в каком приближении к реальности они находятся.

Подавляющее большинство моделей (некоторые из них мы будем рассматривать далее), как это пи странно, описывают, в основном, работу блока принятия решения. Практически мы не можем назвать ни одной модели, специально анализирующей процесс, который является главным при описании психического отражения, именно - особенности оператора преобразования физических характеристик множества внешних сигналов в их психические образы. Ясно, что в таком случае довольно сложно говорить о том, как моделируется процесс трансформации внешних воздействий в психические образы и о том, каковы особенности этой трансформации.

Итак, оказывается, что основные модели различным образом описывают работу блока принятия решения. Наиболее веским аргументом в пользу именно такого рассмотрения сенсорных процессов является, на наш взгляд, следующее положение. Ситуация, которая возникает при обнаружении и различении сигналов, затрагивает очень малую область изменения внешних воздействий. Другими словами, это - ситуация, когда от наблюдателя требуется заметить некоторые, относительно небольшие отклонения параметров внепших сигналов. Поскольку, как уже отмечалось ранее, вопрос о свойствах оператора преобразования сводится к вопросу об организации и метрике сенсорного пространства, постольку в данной ситуации при некоторых простых предположениях мы можем допустить линейное представление рассмотренного выше оператора. Тогда проблема отображения фактически снимается, так как между множествами внешних воздействий и их психических образов постулируется в первом приближении линейная связь, а это может означать простое изменение масштаба результата отображения. В этом случае задача резко упрощается. Результат отображения простого одномерного воздействия мы будем обозначать далее как хⁱ_s и ось x_s будем интерпретировать прямо в терминах сенсорных образов. Проблема отображения теперь сводится просто к тому как определять и фиксировать расстояние на указанной оси. Эта проблема решалась в существующих моделях обнаружения и различения при помощи некоторых разумных постулатов, которые, однако, потенциально подвержены критике (и в действительности критиковались с позиций психофизического шкалирования).

Но прежде чем перейти к обсуждению самих моделей, мы бы хотели напомнить некоторые экспериментальные факты и те эмпирические характеристики, которые выделены при исследовании сенсорных процессов в рассматриваемом аспекте.

Во-первых, речь идет об известном свойстве вариативности реакций, которое часто интерпретируется как следствие вариативности значений S в множестве сенсорных образов или как доказательство вариативности ответов сенсорной системы на постоянное внешнее воздействие (см. прежде всего [25]).

Во-вторых, это экспериментально наблюдаемое наличие некоторого порога срабатывания наблюдателя, т. е. наличие некоторой критической точки (зоны) разделения, именно - той границы, которая позволяет нам разделять ответ "да" и ответ "нет". Значит, следует предполагать, что в самой сенсорной системе в целом существует некая точка, которая позволяет вырабатывать такие ответы.

Эти два факта вместе с их интерпретацией позволяют нам изобразите ситуацию обнаружения или различения в множестве x_s так, как показано на рис. 2. В связи с тем, что множества, которые мы пока не интерпретируем строго, имеют некоторую область пересечения, ситуация оказывается не вполне определенной. Здесь существует принципиальная возможность получения ошибочных ответов; по логике самой ситуации реакции наблюдателя или любой другой решающей системы должны быть связаны с ошибкой. Напомню, что расщепление множества ответных реакций здесь особой роли не играет. Если даже, например, мы введем сомнительные ответы как еще один класс допустимых ответов, то получим теоретически ту же самую картину, но уже для большего количества реакций (см. рис. 3).

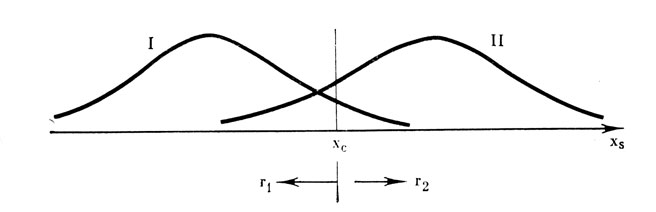
Рис. 2. Изображение ситуации обнаружения или различения в сенсорном пространстве при двух допустимых реакциях r₁ и r₂ ∈ R

И, наконец, третий важный факт заключается в том, что на результаты деятельности наблюдателя влияют вероятностные характеристики внешнего воздействия. Наличие априорной информации, так же как и информации в виде обратной связи, изменяет поведение наблюдателя. Таким образом, практически любая информация, поступающая из внешней среды, может в значительной мере определять изменение ответов наблюдателя.

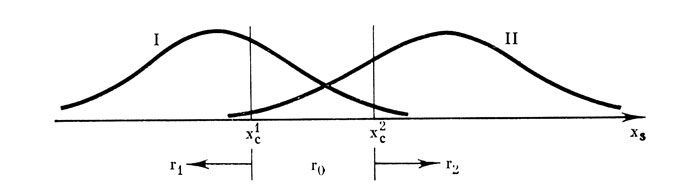
Рис. 3. Изображение ситуации обнаружения при трех допустимых реакциях r₁, r₀ и r₂ ∈ R

Вот те основные факты, которые были выявлены в процессе исследований сенсорных процессов и которые необходимы для дальнейшего изложения материала.

Коротко оценивая историю развития моделей, мы позволим себе выделить две главные группы моделей, которые были построены в результате многочисленных исследований сенсорных процессов [2, 9, 16, 18]. Эти две главные группы образуют модели, которые являются, в известном смысле, продолжением уже традиционного спора о том, существует или не существует собственный порог сенсорной системы. В них порог рассматривается, с одной стороны, как произвольно регулируемая разделяющая граница, а с другой - как собственная, хотя и флуктуирующая, характеристика сенсорной системы.

Во всяком случае, феноменально пороговой или некоторой разделяющей "границей в одной группе моделей объявляется та пороговая характеристика, которая обосновывается в традиционных представлениях как пятидесятипроцентная (или иногда в модификациях метода - семидесятнпятипроцентная) точка на кривой накопленных частот ответов (см. рис. 4). Однако в этих моделях она, эта точка, рассматривается как операционная характеристика наблюдателя.

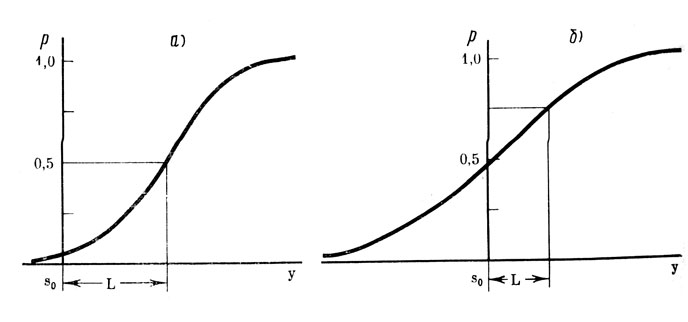
Рис. 4. Кривая частот накопленных ответов в психофизическом пороговом эксперименте по различению (психометрическая кривая). а - для метода констант при трех категориях ответов. Порог определяется как точка, соответствующая р=0,5; б - то же для двух категорий ответов. Порог L определяется как точка, соответствующая р=0,75

Другие модели исходят из принципа дискретности как основного принципа работы сенсорной системы, т. е. пороговые свойства рассматриваются как внутренне присущие сенсорной системе, и сама сенсорная система описывается как более или менее сложный пороговый элемент. Это означает, что есть определенный порог срабатывания сенсорной системы: в пределах кванта между двумя соседними порогами все внешние воздействия и раздражения оказываются неразличимыми и одинаково сигнальными или несигнальными. Величины этих порогов соответствуют ненулевым энергиям внешних воздействий.

К первой группе моделей относится, в частности, широко известная модель Светса [17] и некоторые другие, разработанные в рамках радиотехнической статистической теории обнаружения сигнала. На рис. 2 приведена ситуация распределения сенсорных событий при обнаружении сигнала в интерпретации указанных моделей.

Ко второй группе относятся несколько весьма разноплановых моделей, например, такие, как нейроквантовая модель Стивенса и др. [16], высокопороговая модель Блеквелла [14], модель Люса [19]. На рис. 5 приведена возможная иллюстрация распределения сенсорных событий для предположений модели Люса.

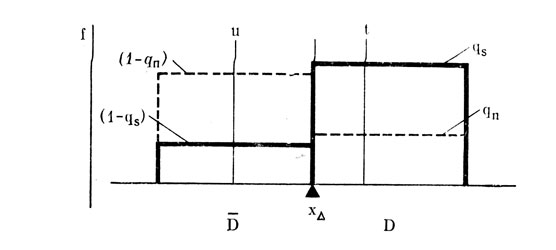
Рис. 5. Возможная иллюстрация распределения вероятностей сенсорных событий в модели Люса. Ось абсцисс не имеет отчетливой интерпретации в терминах сенсорных событий. Параметры t и u объясняются в тексте

В качестве примера моделей первой труппы мы частично рассмотрим нашу редакцию модели, разработанной в рамках статистической теории обнаружения сигналов в психофизике [5]. Эта модель предполагает следующее. Эффекты от внешних воздействий в сенсорной системе распределены нормально и аддитивны. Внешние помехи представляют собой белый шум. Оператор преобразования внешних воздействий в субъективные впечатления линеен относительно математических ожиданий эффектов в сенсорном пространстве.

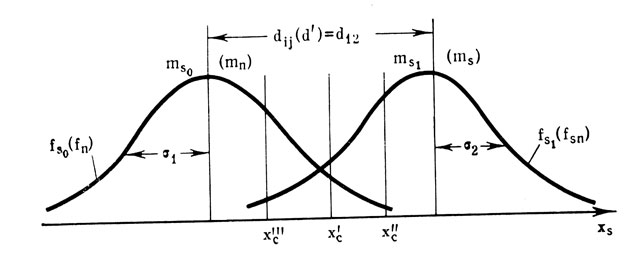
Рис. 6. Иллюстрация ситуации обнаружения (символы в скобках) и различения сигналов в сенсорном пространстве для моделей первой группы

Тогда события в сенсорном пространстве при обнаружении строго детерминированного единичного сигнала на фоне шума могут быть описаны с помощью двух распределений (см. рис. 6). Одно распределение f_n - описывает сенсорные эффекты от внешнего шума, второе - f_Sn - от смеси сигнал + шум. Необходимо отметить, что впервые аналогичная интерпретация сенсорных событий для несколько отличного класса задач была предложена в работах Терстона [25, 26]. Ее фактическое развитие в работах Светса и др. было предпринято без ссылки на Терстона и связано с отказом от некоторых важных с точки зрения психофизики предположений Терстона. Выдвинутые Светсом и другими новые предположения в ряде случаев оказываются менее приемлемыми.Одновременно, Терстон предложил рациональный способ оценки сенсорных расстояний между двумя сенсорными событиями, которые описывают математическое ожидание сенсорных эффектов внешних воздействий; это расстояние строится в терминах стандартных отклонений распределений сенсорных событий:

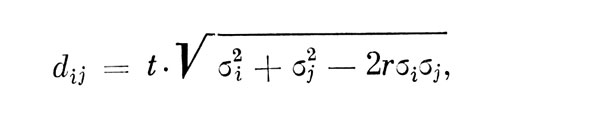
где t=Ф^-1(р) (Ф^-1(р) обозначает оператор нахождения аргумента нормального распределения, р - частота предпочтения S_j к S_i); r - коэффициент корреляции S_i и S_j. Таким образом, удобной мерой сенсорных расстояний является величина d_ij=F(S_j)- F(S_i)/σ_ij, нормированная по стандартному отклонению %. Так, вместе с предположением о линейности оператора отображения F внешних воздействий в сенсорные эффекты, решается вопрос о метрике оси xs (рис. 6). Если обозначить оператор отображения F (S), то метрика d{j в одномерном случае дает:

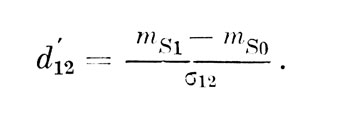
Для ситуации простого обнаружения детерминированного сигнала на фоне белого шума имеем (с учетом результата, описанного в работе [6]):

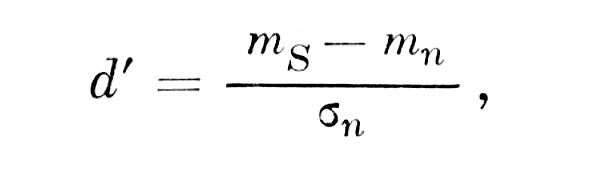
что в точности совпадает с гипотетической мерой Светса и другими.

Пусть в ситуации, изображенной на рис. 6, существует некоторая критическая точка х_с, разделяющая множество х_S на два подмножества в соответствии со следующим правилом δ:

если х_S≤х_с, то следует отвечать "нет";

если х_S≤х_с, то следует отвечать "да".

Тогда задача становится вполне понятной и может быть описана формально. Понятно, что реализация записанного выше правила связана с работой блока решения, изображенного на рис. 1. Это правило будем называть правилом принятия решения наблюдателя в задаче простого обнаружения в процедурах с двумя допустимыми ответами. Понятно также, что порогом наблюдателя в операционном смысле является величина внешнего воздействия, соответствующая положению разделяющей границы или критической точки х_с на оси х_S. Сама критическая точка делит множество всех сенсорных эффектов x_S так, что все впечатления, величины которых не больше х_с относятся наблюдателем к помехе и вызывают ответ "нет, сигнала не было"; все значения x_S, превышающие х_с относятся к впечатлениям от сигнала и вызывают ответ "да, сигнал был".

Таким образом, если в рассматриваемой ситуации существует ненулевое пересечение распределений f_n и f_sn, то существуют четыре возможных исхода наблюдения: правильное обнаружение у/s, пропуск сигнала n/s, ложная тревога у/n и правильное отрицание n/n. Наличие такого пересечения и составляет существенную особенность всех пороговых ситуаций, в том числе и ситуации обнаружения.

Мы уже говорили о том, что в данной ситуации нет возможности выполнить однозначное и правильное разделение множества сенсорных событий. Принципиально возможны различные положения разделяющей границы на оси х_S, например х_с, х"_с, х"'_с и т. д. (см. рис. 6). Анализ моделей позволяет утверждать, что положение разделяющей границы, определяющее результат наблюдения, зависит не только от характеристик указанных множеств на оси x_s, но также от априорной информации о вероятности появления сигнала и от заданной объективно (или выработанной) субъективной значимости или стоимости результатов наблюдения (т. е. каждого из исходов наблюдения, указанных выше). Как ясно видно из рис. 6, одновременная максимизация обнаружения и минимизация ошибок при заданном распределении событий невозможна. При уменьшении ошибок ложной тревоги увеличивается количество пропусков и наоборот. Таковы свойства объективной ситуации.

Перераспределение значимости исходов обнаружения или перераспределение анриорных вероятностей может привести к сдвигу критической точки х_c в ту или другую сторону, однако, не вполне ясно, почему это происходит и как именно движется разделяющая граница. Вопрос заключается в том, как все-таки наблюдатель решает эту задачу.

Ответ на поставленный вопрос предполагает, что наблюдатель выбирает тот или иной критерий оценки эффективности собственной деятельности, и этот критерий находит свое отражение в моделях, которые внимательно рассматривает процесс решения. Можно показать, что единственным важным требованием к критерию решения в разных моделях является требование унимодальности некоторого функционала К, описывающего критерий оценки на множестве x_S, или на некоторых заранее определенных подмножествах его. Понятно, что таких критериев можно найти великое множество, и новый вопрос заключается в том, каким критерием реально пользуется человек-наблюдатель в реальных задачах такого типа.

Большинство моделей первой группы, которые мы рассматриваем в этой части работы, задают критерий эффективности решения внешним образом, исходя из некоторых разумных соображений. После этого на модели и в экспериментах рассматривается, как должен и как меняется реально операциональный порог или положение разделяющей границы на сенсорной оси при изменении значимости (стоимости) различных исходов наблюдения или при изменении вероятностей появления сигнала и шума. Это известные результаты, и заинтересованному читателю можно рекомендовать указанные ранее обзоры [2, 16, 18} и монографии [17].

Итак, мы вкратце завершили описание моделей первой группы на примере одной обобщенной редакции модели обнаружения. В чем заключаются наиболее принципиальные допущения, в чем можно видеть психофизическую содержательность модели, что положено в основу ее рассмотрения?

Эти вопросы достаточно важны, поскольку дальше идет обычная формализация, результаты которой могут быть верны или не верны, полезны или нет, в зависимости от того, как даны и что содержат ответы на эти вопросы.

Прежде всего, выясняется, что в данной модели сенсорная система не обязана иметь собственного порога, существенно ограничивающего психологическое содержание сенсорного материала, поскольку предполагается непрерывность множества х_S в локальной пороговой области сенсорного пространства. Операциональный и - феноменологический - порог х_с есть построенная на этом непрерывном множестве x_S разделяющая граница двух классов эффектов.

Второе допущение предполагает, что впечатления от шума и сигнала нормально распределены, т. е. что сенсорные образы шума и смеси сигнал + шум таковы, что их значения в множестве х_S подчиняются гауссовскому распределению плотности вероятностей. Кроме того, впечатления от сигнала и шума аддитивны, некоррелированы и имеют одинаковую дисперсию. Последнее, впрочем, не является критическим, так как можно рассмотреть случай, когда сигнал имеет собственную нестабильность, является нормально распределенным по уровню, и тогда дисперсия смеси будет возрастать с ростом сигнала [5].

Можно показать, что все эти допущения являются фактическим следствием, в большинстве случаев неявного, предположения о линейности оператора отображения внешнего воздействия в сенсорное пространство и выбранной модели сигнального входного процесса [5].

Другой класс допущений связан с представлением о роли решения в детерминации поведения. Здесь предполагается, что правило принятия решения фиксировано и известно экспериментатору или исследователю. За исключением работы Забродина [5] предполагается также, что критерий эффективности решения фиксирован и известен. При этом для работы модели (и наблюдателя) необходимо знание априорных вероятностей входных событий и внешним образом заданных стоимостей возможных исходов наблюдения. Тогда условием устойчивой работы наблюдателя является работа в области экстремума выбранного функционала K, описывающего критерий эффективности решения.

Таковы наиболее существенные допущения, положенные в основу рассматриваемого варианта модели работы наблюдателя в задаче обнаружения. Насколько верно и полно они охватывают существенные особенности сенсорных процессов, настолько этот вариант модели или его модификации приемлемы для психофизика.

Можно выдвинуть следующие возражения против моделей, изложенных выше.

Во-первых, в таком описании модели дается, к сожалению, только интегральный результат деятельности, т. е. не может быть учтена вероятная внутренняя динамика процесса. Эксперименты, которые служат основным подтверждением моделей этой группы, в подавляющем большинстве случаев проводятся на тренированных наблюдателях. Мы склонны предполагать, что в этих случаях человек-наблюдатель искусственно "загоняется" в рамки того критерия, который выбран исследователем. В то же время лучшие экспериментальные результаты отличаются от теоретических предсказаний примерно на 3-6 децибел. Однако это количественное расхождение не слишком большое, и оно скорее всего связано с целым рядом дополнительных предположений, принятых при построении модели "идеального наблюдателя" на базе рассмотренной модели сенсорных процессов. Это расхождение связано с неверными оценками параметров ситуации и самой модели в той части, которая касается свойств оператора отображения внешних воздействий в сенсорное пространство.

Может вызвать сомнение предположение о непрерывности и гауссовом характере сенсорных впечатлений, поскольку в любом случае они представляют собой либо результат интегрирования импульсных нервных процессов, либо сами эти процессы, особенно в случае сенсорных шумов. Кроме того, характеристики этих образов существенно нестационарны [3, 12]. Вероятно, если в реальном процессе действует достаточно большая популяция элементов системы, можно допустить и непрерывность множества х_S и нормальное распределение характеристик сенсорных образов (в том числе, собственного шума сенсорной системы). Однако там, где емкость воспринимающей системы мала, вероятно, нельзя говорить ни о нормальности, ни о непрерывности x_S. В свое время мы предлагали [5] ввести такое понятие, как непрерывность сенсорной оси почти наверное. Это означает, что с течением времени любое значение сенсорного эффекта может возникнуть с вероятностью, близкой к единице.

Теперь рассмотрим вопрос о критерии эффективности решения К. Наши эксперименты и анализ других данных [7] показывают, что наблюдатель не всегда придерживается фиксированных критериев, принятых в моделях обнаружения сигнала [15, 17]. Если наблюдатель работает в естественных условиях, то он не обязательно использует критерий, принятый в упомянутых выше моделях. Если наблюдатель находится в условиях эксперимента, то он может начать работать с более простым и/или более привычным ему критерием, и только затем в процессе эксперимента может перейти к критерию, заданному схемой эксперимента,- в процессе обучения и/или под влиянием экспериментатора.

Возникают, таким образом, две дополнительные задачи: во-первых, анализ собственных характеристик решающей системы наблюдателя, а во-вторых - анализ процесса обучения. Первая задача более подробно описана в работе Забродина [11]; при обсуждении второй следует прежде обратиться к моделям второй из выделенных ранее групп.

Вторая группа моделей рассматривает, в некотором смысле, противоположные свойства сенсорных процессов. Наиболее представительный вариант такой модели был предложен Р. Люсом [19], и он в настоящее время расценивается как классический вариант моделей обучения в сенсорных процессах, совпадающий по духу с идеями Эстеса, Аткинсона и других, (смотри, например, [1]).

Эта модель рассматривает обучение наблюдателя в общих чертах в той же схеме решения, что и предыдущие, но при этом частично отвлекается от того, какова действительная природа сенсорных событий и каковы их характеристики, т. е. отказывается от анализа свойств множества x_S. В модели Люса вводятся лишь два возможных состояния сенсорной системы, определяемые ее собственным порогом и интенсивностью входного сигнала: состояние обнаружения D и иеобнаружения D, соответственно (см. рис. 5).

Таким образом, постулируется наличие собственного порога сенсорной системы x_Δ, делящего эффекты всех возможных воздействий на два класса D и D. В таком случае, отвлекаясь от внутреннего содержания сенсорной информации, Люс (и некоторые другие) предполагает неразличимость сенсорных событий в указанных областях D и D в полном соответствии с логикой пороговой концепции. Это утверждение в некотором смысле эквивалентно предположению о прямоугольном характере плотностей распределения вероятностей сенсорных событий - ответов сенсорной системы на внешние воздействия.

Если вслед за Люсом признать возможность превышения порога впечатлениями от шума с вероятностью q_n, и впечатлениями от сигнала с вероятностью g_s, превышающей q_n, то ситуация простого обнаружения, которую мы анализируем в настоящей работе, будет выглядеть в точности так, как показано на рис. 5. При этом ось абсцисс, по-видимому, не имеет отчетливой интерпретации в терминах собственно сенсорных событий. Отвлекаясь от собственных характеристик сенсорного пространства (за исключением признания порога и вероятностных описаний классов D и D), указанные исследователи используют эту модель в дальнейшем для построения динамики некоторого решающего механизма наблюдателя в задаче сенсорного научения при обнаружении. Необходимым условием работы модели и наблюдателя в данном случае является наличие обратной информации и подкрепления ответов наблюдателя. В качестве подходящего математического аппарата выбраны линейные рекуррентные алгоритмы, предложенные для психологических задач в работах Буша, и Мостеллера [4].

Общая логика работы такого механизма описывается в виде следующих соотношений:

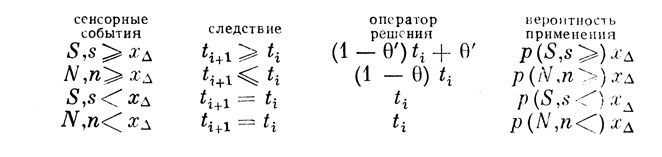
Здесь s - сигнал, n - шум, S, n≥x_Δ - состояние обнаружения, S, n<x_Δ - состояние необнаружения. θ', θ - параметры подкрепления, i - шаг. t обозначает некоторый параметр решающего механизма, который в данном случае в точности совпадает с вероятностью ответа "да", если сенсорная система находится в состоянии обнаружения D. Совершенно аналогичная схема составляется для оператора и, который также совпадает с вероятностью ответа "да", но в случае, если сенсорная система находится в состоянии необнаружения D.

Поскольку сенсорные события неразличимы между собой как в состоянии D, так и в состоянии D, указанные операторы t и u фактически описывают работу механизма решения в ситуации вероятностного угадывания. В этом случае наблюдатель рассматривается как играющий автомат, а сама модель может быть с равным успехом применена к ситуациям вероятностного прогнозирования последовательностей двух событий.

Как мы видим в случае простого обнаружения, состояния сенсорной системы исчерпываются парой D и D. Поэтому полное описание поведения наблюдателя в данной задаче исчерпывается системой двух зеркально отображающих друг друга схем типа приведенной выше. В стационарном режиме работы при достаточной длине последовательности входных событий, т. е. при неизменных вероятностях входных событий p_s и р_n и при неизменных параметрах подкрепления, операторы t и u описываются аналогичными условиями перехода от i-гo шага к i+1, а последовательность реакций наблюдателя представляет собой две независимых марковских цепи (для состояний D и D, соответственно). Условие перехода для t записывается в следующем виде:

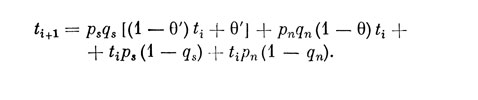
Предельный преход к установившемуся режиму при t->∞ дает следующее значение для математического ожидания t:

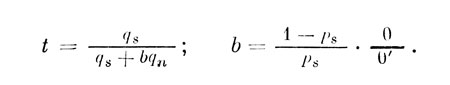
Обсуждая основные особенности модели, напомним еще раз, что в основу модели были положены допущения о строго пороговом принципе работы сенсорной системы и неразличимости сенсорных событий в окрестности порога в пространстве сенсорных событий.

Не вдаваясь в детальный анализ модели, отметим наиболее существенные и попятные психофизику соображения, связанные с изложенным выше пониманием работы наблюдателя.

Экспериментальные результаты, полученные на тренированных наблюдателях, показали, в частности, что пороговая модель Люса и модель, построенная Светсом и др. в рамках статистической теории обнаружения сигнала, дают одинаково хорошее описание поведения наблюдателя. Во всяком случае обычные методы статистической проверки не позволяют отдать предпочтение ни той, ни другой.

Таким образом, вопрос о существовании порога сенсорной системы пока остается открытым. Однако существуют некоторые веские соображения о серьезных проблемах внутри самой модели Люса. В частности, неясно, каким образом происходит переход от работы наблюдателя в области обнаружения D к области необнаружения D. Из модельного описания, заключающегося в решении двух указанных выше схем работы решающего механизма, такой переход никак не следует. Точка х_Δ - собственного порога сенсорной системы является критической точкой для предложенной системы алгоритмов и не допускает перехода из D в D. Поэтому необходим дополнительный внемодельный механизм, обеспечивающий этот переходный скачок из D в D и обратно. В то же время такой переход достаточно легко осуществляется реальным наблюдателем, судя по экспериментальным данным.

Поскольку необходимым условием работы такой модели является наличие подкрепления и обратной информации, постольку неясно, как может самообучаться реальный оператор. Однако такое самообучение мы наблюдаем в любой экспериментальной ситуации сходного типа.

Наконец, несмотря на то, что фундаментальной характеристикой модели Люса являются именно динамика научения, к сожалению, нет реальной возможности проследить сам факт обучения в модели, ибо она, как и модели статистических теорий обнаружения, основное внимание уделяет интегральным конечным результатам научения, - в конечных формулах параметр обучения явно не присутствует - дано лишь отношение параметров подкрепления θ и θ'.

Отмеченные выше проблемы, возникшие при сравнительном анализе истории развития моделей обнаружения в психофизике, частично снимаются в наших работах [3, 5-10]. Так, например, в качестве исходных предположений были выбраны следующие:

- субъективное сенсорное пространство обладает динамичной топологией и метрикой, которые подчиняются, в известной мере, условиям поставленной задачи наблюдения;

- оператор отображения внешних воздействий в сенсорные образы F (x_s/s) изотопен и действует так, что сенсорные оси непрерывны почти наверное; понятно, что и сам оператор может зависеть от структуры решаемой задачи (это следует частично из предыдущего);

- результаты работы наблюдателя в неопределенной ситуации, например, при наличии ненулевого пересечения образов входных воздействий при обнаружении и различении, определяются особенностями блока решения;

- блок решения обеспечивает выбор подходящих правил решения и критериев оценки эффективности наблюдения под влиянием внешних и внутренних источников информации; при этом внешние объективные условия и внешняя информация являются ведущей детерминантой работы блока;

- реальный наблюдатель работает оптимально, точнее субоптимально в смысле некоторого функционала, отражающего принятый им критерий качества; работа блока решения строится с учетом всей входной информации, следовательно, функционал качества определяется на множестве сенсорных образов входных воздействий с учетом внешней и внутренней внесепсорной информации.

Понятно, что блок решения выбирает потенциальные результаты решения, оценивает их и возможные способы их достижения. Выбранные потенциальные результаты реализуются некоторым выходным оператором, который известным образом отображает множество выбранных и допустимых потенциальных результатов на множество реальных результатов - ответных реакций. В простейших случаях можно полагать этот оператор оператором взаимнооднозначного отображения или даже рассматривать его как оператор тождественного преобразования F (r/r_s).

Теперь, если взять в качестве исходного то представление о сенсорных событиях, которое было показано на рис. 6, то с учетом наших основных предположений и тех замечаний, которые были высказаны ранее при описании и анализе рис. 6, можно кратко записать формальный вид модели применительно к пороговым задачам:

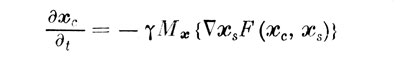
или в дискретном времени:

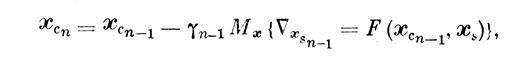
где n - интервал времени с начала работы; х_с - текущее значение разделяющей границы в сенсорном пространстве, γ - параметр обучаемости, точнее, показатель адаптивных способностей системы наблюдения, М_х {•} - знак оценки математического ожидания по доступной наблюдателю статистике сенсорного образа входных событий, F (x_c, х_s) - функционал, отражающий оценку качества решения при текущем значении разделяющей границы.

В данной модели х_с описывает положение разделяющей границы в векторной форме, поскольку рассматривается многомерный случай. Условие оптимальности обеспечивает остановку движения разделяющей границы в области экстремума математического ожидания функционала качества, как это легко видеть из приведенных выше формул. Целесообразно потребовать, чтобы экстремум функционала качества находился в области пересечения сенсорных образов разделяемых классов событий и учитывал статистику этих сенсорных образов.

Можно показать, что сами статистические описания сенсорных образов при некоторых дополнительных ограничениях на свойства оператора отображения внешних воздействий могут быть построены с помощью алгоритма, аналогичного тому, который получается при дискретном времени для х_сn. В этом случае алгоритм поиска разделяющей границы, что в общем естественно, работает на более высоком уровне, используя результаты алгоритма, строящего сенсорный образ. Тогда функционал качества, как это показано в нашей работе [5] целесообразно выбирать в виде среднего суммарного взвешенного расстояния от положения разделяющей границы до центров сенсорных образов разделяемых классов событий:

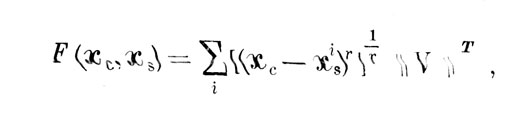
где r - натуральное число, ¶V¶^T - транспонированная матрица весовых коэффициентов. Там же показано [5], что реальные наблюдатели работают с критериями, для которых r=1, 2. В другой работе [7] показано, что при надлежащем выборе F (x_c, х_s) и при изменении только матрицы субъектившлх стоимостей наблюдения можно получить разные известные критерии оптимального наблюдателя. Так, например, для r=1 функционал качества можно привести к следующему виду:

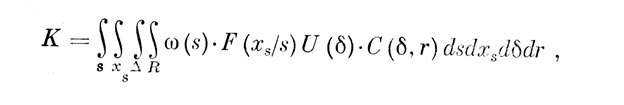
где ω (s) - функция характеризующая статистику входных воздействий, ω (s)=p_sf_sn+(1- р_s)f_n; F_s(x_S/S) - оператор отображения объективного входного воздействия в его субъективный сенсорный образ; U (δ) - функционал на множестве решающих правил δ; С (δ, r) - определенная на множество Δ X R матричная функция веса или стоимости исходов наблюдения; R - множество допустимых выходных реакций.

Используя указанный функционал К для описания приведенной выше ситуации обнаружения сигнала при допущении линейности оператора F (x_s/s), можно получить оценки граничных условий, при которых предложенная здесь модель наблюдателя в точности совпадает с моделью типа Люса. При других ограничениях эта модель в точности совпадает с моделью типа Светса и др.

Резюмируя изложенный в данной работе материал, необходимо еще раз подчеркнуть полезность применения и анализа математических моделей в целях психологического исследования. Так как математические модели и их основания в наиболее чистом виде отражают теоретические представления авторов об особенностях и природе моделируемых феноменов, теоретическая и экспериментальная проверка и анализ основных допущений и предположений моделей позволяют значительно глубже проникнуть в существо самих моделируемых процессов.

Поиск формальных описаний, инвариантных в широком классе условий, дает возможность найти фундаментальные законы самих явлений. Оценка параметров формальных описаний позволяет построить систему количественных признаков, допускающих адекватное измерение и сравнение реальных моделируемых объектов. Оценка инвариантности выделенных параметров для одного и того же реального объекта в разных условиях и задачах функционирования открывает подход к установлению закономерных связей и отношений в исследуемых явлениях. Наконец, как в нашем случае, построение новых моделей намечает перспективную программу экспериментальных исследований, взаимосвязанных в рамках конкретной теоретической концепции.

Ближайшие задачи теоретических и экспериментальных исследований в области сенсорной чувствительности направлены на дальнейшую проработку рассмотренных выше проблем.