3. Энергетическая статистическая теория

Эта, излагаемая ниже, теория базируется на основных свойствах слухового анализатора, именно на способности суммировать по частоте и по времени, а также на статистическом характере связи между стимулом и вызванным им ощущением.

3.1. Свойства анализатора. Прежде чем переходить к построению теории, остановимся коротко на основных свойствах слухового анализатора.

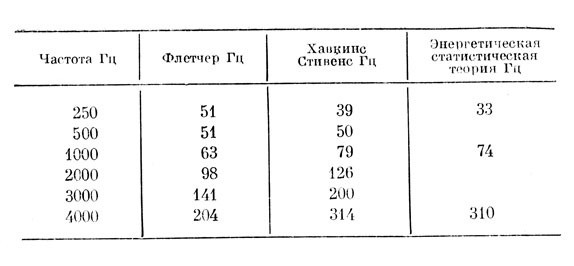
3.1.1. Суммирование по частоте. Известно, что маскирующее действие на синусоидальный сигнал оказывают не все спектральные составляющие шума, а лишь те из них, которые попадают в относительно узкую область вокруг маскируемого тона; эти спектральные компоненты оказывают суммарное действие при маскировании тона, что выражается известной концепцией критических полос, выдвинутой Флетчером [7]. Величины критических полос для разных" частот, экспериментально полученные Флетчером, приведены в таблице вместе с примерно такими же данными, полученными в работе Хавкинса и Стивенса [13]. Другие экспериментальные данные близки к упомянутым, однако некоторые превышают их более чем в два раза [28]. Подробные сведения по этому вопросу на русском языке можно найти в достаточно полном обзоре [4]. Здесь хотелось бы добавить следующее.

Причина упомянутых расхождений, на наш взгляд, прежде всего в двойственном характере определения критической полосы, данном Флетчером. С одной стороны, это - та ширина полосы, уменьшение которой начинало приводить к уменьшению маскирующего действия шума (при его неизменной спектральной плотности мощности). С другой стороны, это - частотная полоса, в которой мощность шума равна мощности тона на пороге маскировки. Флетчер полагал эти два определения тождественными. Однако некоторые данные (см. [4]) позволили выдвинуть гипотезу о фильтре уха, рассматривая его не как идеальный полосовой фильтр, а как RLC фильтр, с плавным затуханием на краях полосы пропускания. Если принять эту гипотезу, то определения Флетчера нельзя считать тождественными, и становится понятным расхождение результатов, полученных при следовании разными экспериментальными путями, продиктованными этими двумя определениями. Действительно, расчеты показали, что ширина эквивалентной полосы такого RLC фильтра, рассчитанная по экспериментальным данным, имеющим завышенный характер, хорошо согласуются с экспериментальными данными Флетчера, Хавкинса и Стивенса (табл.) и других. [4]. Это дает основание полагать, что маскирующее действие шума может оцениваться произведением его спектральной плотности мощности на ширину критической полосы, примерные значения которой даны в первых двух столбцах упомянутой таблицы.

Объективность требует отметить, что существует и другая точка зрения, согласно которой расхождение экспериментальных результатов объясняется действием некоторого механизма настройки; этот механизм можно представить в виде фильтра, меняющего свои характеристики в зависимости от задачи [4]. Отсюда непосредственно последовал вывод о том, что понятие критической полосы, равно как и ее измерение, вообще не имеет смысла [23]. Эта гипотеза, выдвинутая авторами теории обнаружения в психофизике, была для них весьма утешительной, поскольку оправдывала игнорирование, при построении теории, концепции критических полос.

3.1.2. Суммирование по длительности. Экспериментальный оныт показывает, что слышимость звука зависит от его длительности. Измерение абсолютных порогов тональных импульсов показало, что при уменьшении длительности импульса для его слышимости необходимо увеличение интенсивности. На рис. 3 представлена усредненная нами по восьми различным исследованиям (см. библиографию к работам [5, 27]) кривая слышимости тонального импульса в зависимости от его длительности: на оси ординат отложена логарифмическая величина отношения интепсивностей Е_τ/Е_∞, где Е_∞ - интенсивность стационарного тона, Е_τ - интенсивность стационарного тона, из которого вырезан тональный импульс длительностью τ. Аналогичная кривая получена при обнаружении тонального импульса на фоне шума (см. библиографию к работам [5, 6]).

Оказалось, что при длительностях тонального импульса менее 0,1 с указанная зависимость (рис. 3) представляет собой отрезок прямой с наклоном примерно 3 дб на удвоение длительности. Это показывает, что решающим фактором слышимости кратковременных тональных импульсов является энергия сигнала, т. е. произведение интенсивности сигнала на его длительность; уменьшение длительности вдвое компенсируется увеличением интенсивности вдвое, т. е. на 3 дб.

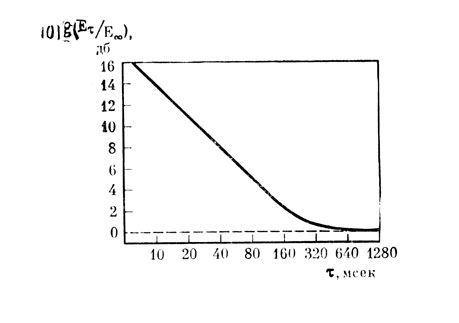
Рис. 3

Ряд экспериментов [10, 16] показал, что обнаружение тонального импульса длительностью до примерно 0,1 с действительно определяется его энергией: при сохранении неизменным произведения интенсивности на длительность порог обнаружения не изменялся.

Эта особенность слухового анализатора позволила сделать предположение о его интегрирующей способности, наиболее наглядным подтверждением которой является эксперимент по оценке слышимости двух коротких импульсов [29]; абсолютный порог слышимости последовательности из двух импульсов с временным интервалом менее 0,1 с не зависел от величины этого интервала и был ровно на 3 дб ниже, чем при относительно больших (более 0,5 с) временных интервалах.

Представление о слуховом анализаторе как об интеграторе звуковой энергии, справедливое для коротких тональных импульсов, плохо описывало, однако, свойства анализатора при больших длительностях импульсов. Наиболее правдоподобное объяснение этому явлению дал еще Мансон [18]. Предположив интегрирующую способность центральной нервной системы, он показал, что отклонение от закона интегрирования может быть вызвано адаптационным эффектом при передаче импульсов по нервному волокну. Эта гипотеза была впоследствии развита и подтверждена топкими физиологическими экспериментами (см. библиографию к работе [22]).

Из сказанного понятно, почему в обнаружении используются кратковременные тональные импульсы (обычно 0,1 с): слышимость таких импульсов хорошо оценивается энергетически.

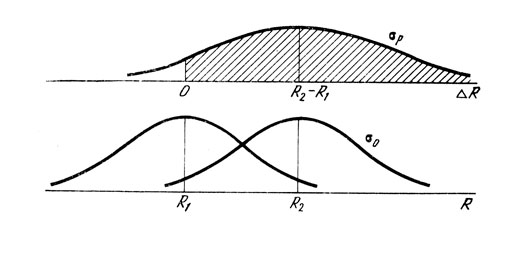
Рис. 4

3.1.3. Статистический характер ощущений. Терстоном [26] была создана статистическая модель, приложимая к результатам различения сигналов и постулирующая статистический характер связи между предъявленным стимулом и вызванным им сенсорным эффектом. Суть ее состоит в том, что ощущения, вызванные многократным предъявлением наблюдателю одного и того же физически детерминированного стимула (например, тонального сигнала), не фиксированы па сенсорной оси, а распределены на ней но случайному закону. Сравнительная оценка двух стимулов в методе парных сравнений графически иллюстрируется рис. 4. На оси R представлены распределения ощущений от предъявлений двух стимулов; R₁ и R₂ - модальные (наиболее часто встречающиеся) ощущения. Результат сравнения частных ощущений от предъявлений этих стимулов описывается распределением ощущений различия на оси ΔR. Если предъявление пары стимулов вызвало одно и то же ощущение, то ощущение различия равно нулю и различение в этом случае невозможно. Наиболее часто встречающимся ощущением различия будет, естественно, разность между модальными ощущениями (R₂-R₁). Вообще если ощущение различия - положительно (вероятность этого равна площади заштрихованной области под кривой распределения), то, по Терстону, это приводит к правильному суждению относительно величин стимулов, если отрицательно, то к неправильному.

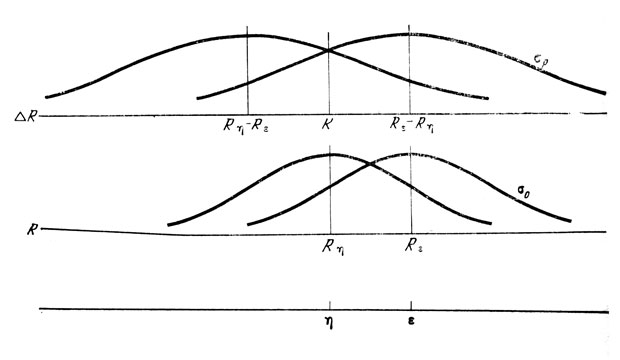
Рис. 5

Психофизическое уравнение Терстона было им дано в следующем виде:

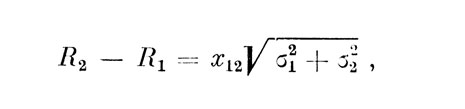
где σ²₁ и σ²₂ - дисперсии ощущений, вызванных предъявлением соответствующих стимулов (для интенсивности звука, как показано в работе [1], σ₁=σ₂), x₁₂ - выраженная в единицах стандартного отклонения величина /?2 - Rlt вычисляемая по доле правильных ответов; другими словами, x₁₂ находится из соотношения

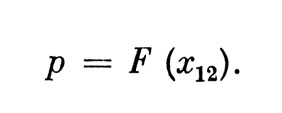
Нетрудно заметить, что психофизическое уравнение Терстона совпадает с выражением для сенсорного расстояния в обнаружении. Действительно, после замены х12 на d' и σ₁, σ₂ на σ₀ уравнение Терстона принимает вид:

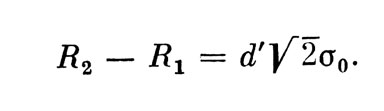
Имея в виду, что для нормальных распределений σp=d'√2σ₀ получаем:

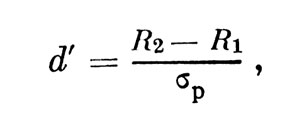
т. е. формулу (1).

Существенное различие между теориями заключается лишь в том, что статистический характер ощущений в модели Терстона связывается не со статистикой сигнала (как в обнаружении), а со случайным характером флюктуации в сенсорной системе.

3.2. Вывод основной формулы. Если теория идеальных наблюдателей, игнорируя свойства анализатора, базировалась исключительно на статистике сигнала, то в основу энергетической статистической теории положено допущение, что случайный характер достаточно широкополосного шума не имеет значения для наблюдателя. Учитывая способность анализатора интегрировать по времени и частоте, случайные колебания шума оцениваются в нашей модели как стационарные с той же спектральной плотностью мощности (Ток шумов на выходе идеального полосового фильтра с шириной полосы Δf, равной критической полосе, будет флюктуировать с периодом Г, равным 1/(0,64Δf) [3]. На частоте 1000 Гц, принимая Δf=70 Гц, имеем Т=20 мс. Эта величина довольно велика, и было бы, строго говоря, неточно утверждать, что энергия шума на выходе полосового фильтра постоянна во времени. Здесь предполагается лишь, что этими флюктуациями можно пренебречь по сравнению с флюктуациями сенсорного характера) и с маскирующим эффектом, прямо пропорциональным энергии шума в критической полосе, т. е. произведению ширины критической полосы на спектральную плотность мощности шума.

Положив, что случайный характер достаточно широкополосного шума на слуховой анализатор влияния не оказывает, мы свели, таким образом, ситуацию обнаружения сигнала на фоне шума к ситуации различения двух сигналов, отличающихся величиной одного параметра.

Методу вынужденного выбора в обнаружении соответствует метод парных сравнений в различении (сравни рис. 1 и рис. 4). Исходя из этого сходства, мы могли бы воспользоваться для дальнейшей формализации выражениями (1) и (2), заимствовав их из теории обнаружения. Нам, однако, нет необходимости апеллировать к сходству этих методов, поскольку, как указывалось выше, психофизическое уравнение Терстона, сформулированное для метода парных сравнений, дает, в единообразной символике, те же формулы.

Связь сенсорной величины R с энергией стимулов может быть установлена следующим образом.

Пусть η и ε - уровни энергии стимулов, отложенные на оси уровней s (рис. 5), а σ_р и σ₀ - физические величины на оси уровней энергии, соответствующие сенсорным величинам σ_р и σ₀. Согласно закону Фехыера (модальное) ощущение пропорционально уровню (логарифму) интенсивности стимула (Закону Фсхнсра в последние десятилетия противопоставляется степенной закон Стивенса; однако он оказался уязвим для критики, и ревизия этого закона, в частности, в отношении экснери. ментов на воспроизведение, сделала его весьма близким закону Фехнера [25]), откуда следует

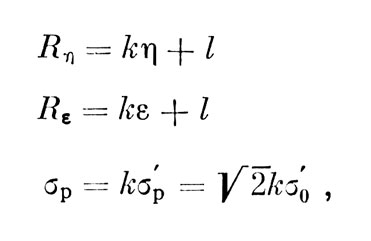
где k и l - константы; для последующих преобразований необходимо, чтобы ар была независимой от уровня интенсивности, что требует выполнения не только закона Фехнера, но и закона Вебера (Действительно, из закона Вебера следует, что Rε-Rη/σ_p=const при ε-η=const. Используя закон Фехнера, имеем k(ε-η)/σ_p=const при ε-η=const. Откуда следует, что σ_р=const).

Из (1), используя последние формулы, получаем искомую связь:

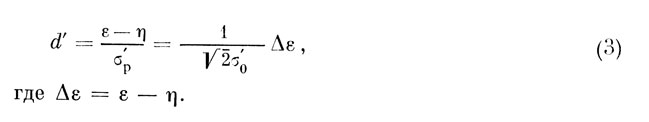
Для конкретизации формулы (3) выразим Ае через входящие туда величины.

Как указывалось выше, маскирующий эффект определяется величиной N_K=N₀•Δf, где Δf - число герц в критической полосе; следовательно N_K можно рассматривать как спектральную плотность мощности шума в Δf раз большую, чем N0, и называть приведенной спектральной плотностью мощности шума. Если интенсивность тонального сигнала (измеренная при достаточно большой его длительности) выражается величиной Е∞, то в случае короткого по длительности (τ) сигнала, его воздействие определится, согласно вышесказанному, энергией τЕ∞.

Наиболее общий вид выражение (3) получит для пьедестал-эксперимента. В этом случае, имея в виду, что сигнал и пьедестал (с энергией, соответственно, E_s и Е_р) - одной частоты и начальной фазы, и, следовательно, когерентны, можно записать:

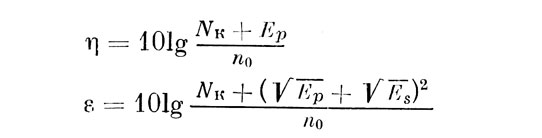
и, следовательно,

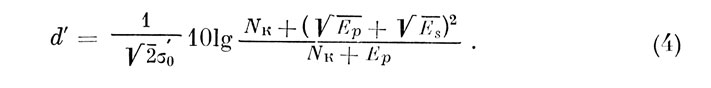
При отсутствии пьедестала (Е_р=0), имеем ситуацию простого обнаружения, для которого

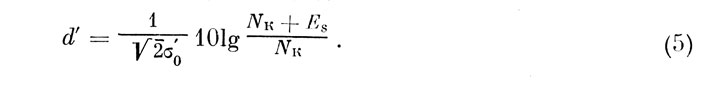
При Е_р>>N_K последней величиной можно пренебречь и мы приходим к выражению для различения двух стимулов:

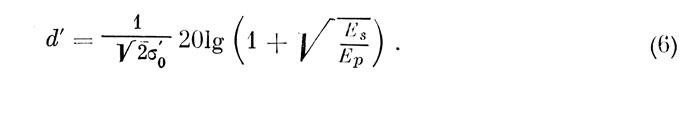
3.3. Качественный анализ формулы. Если Ег> рассматривать как параметр, то наиболее общая форма зависимости d' от E_s (4) представляет собой набор психометрических функций. Оценим крутизну психометрический кривых при изменении параметра (Е_р).

Для простого обнаружения (Е_р=0) при малых E_s/N_K имеем

Для различения при Е_р>>N_K и при малых E_s/N_K имеем:

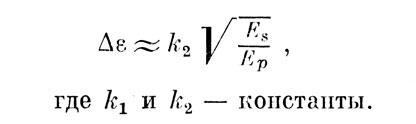
где k₁ и k₂ - константы.

Из последних формул видно, что психометрическая кривая для различения - более пологая, чем для простого обнаружения. Крутизна кривой для пьедестал-эксперимента занимает, очевидно, промежуточное положение.

Изменение величины σ₀ не сказывается на крутизне психометрической кривой; оно лишь сдвигает кривую вдоль оси абсцисс. Действительно, из (5) и (7) для простого обнаружения следует обратная пропорциональная зависимость между σ'₀ (в дб) и Е., (в линейных величинах). Поскольку при построении психометрических кривых на оси абсцисс откладывается уровень сигнала (в дб), постольку увеличение в k раз σ'₀ приведет к сдвигу на - 10 lgk психометрической кривой вдоль оси. Проведя аналогичные рассуждения для различения, получим сдвиг на величину - 20 lgk.

Для качественного анализа взаимного расположения психометрических кривых при изменении параметра (Е_р), достаточно исследовать выражение под знаком логарифма в (4); это выражение можно записать в виде:

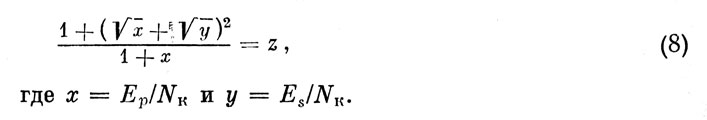
Частная производная от z по х (в предположении, что у=const), имеющая вид

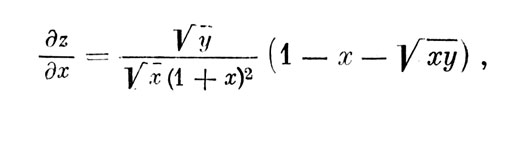
обращается в пуль при условии

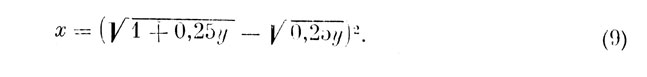
Поскольку при переходе через эту точку производная dz/dx меняет знак с + на - (или, что то же самое, вторая производная по х - отрицательна), постольку (9) дает необходимое и достаточное условие максимума исследуемой функции при каждом фиксированном у.

Подстановка (9) в (8) дает, таким образом, линию максимумов. Из (9) видно, что при любом у найдется некоторое х, при котором (8) достигает максимума по х. При у -> ∞ величина х, удовлетворяющая (9), стремится к нулю; при у -> 0, х -> I. Если х>1, то (8) не имеет максимума по х, так как условие (9) невыполнимо. Отсюда следует, что каждая из кривых при х ≤1 касается линии максимумов, определяемой подстановкой (9) в (8), лишь в одной точке.

Совместное исследование выражений (4, 9, 8) показало, что касание психометрических кривых кривой максимумов в практически важной области р (0,6÷0,9) имеет место при относительно малой величине у. Полагая у=0, из (9) получаем х=1, т. е. кривой максимумов может практически служить психометрическая кривая при х=1 (Е_р=N_K). При этом условии порог обнаружения достигается при наименьшей величине у=E_sN_K (При практически получаемых σ'₀ минимум порога обнаружения (т. е. величина у, при которой соответствующая психометрическая кривая касается кривой максимумов в точке с ординатой 0,75) достигается при х=0,9≈1).

3.4. Определение параметров формулы. Анализ полученных формул показывает, что для их использования необходимо задаться величинами, связанными со свойствами слуха: Δf и σ'₀, поскольку физические параметры - спектральная плотность мощности шума и энергия сигнала - измеряются инструментально.

Однако прежде чем использовать эти формулы, необходимо убедиться в их правомерности или, по крайней мере, в их продуктивности, что удобнее сделать, обратив задачу: по надежным экспериментальным данным определить искомые величины (Δf и σ'₀).

В уравнение (6) входит лишь одна из этих величин (σ'₀), и, следовательно, она может быть определена по результатам экспериментов на различение.

Величина Δf наряду с σ'₀ входит в уравнения (4) и (5). Это дает нам реальную возможность проверить правомерность предложенных формул, вычислив эту величину из результатов эксперимента по простому обнаружению и по пьедестал-эксперименту независимо, с помощью, соответственно, формул (5) и (4). Кроме того, выбрав указанный путь, мы можем оценить, насколько правдоподобны вычисленные величины Δf в сравнении с данными, полученными из прямых экспериментов (табл. 1).

В литературе, описывающей экспериментальные исследования, обычно приводятся величина порога обнаружения. Чтобы использовать эти данные, определение искомых величин будет производится нами также используя пороговые значения.

Для определения величины σ'₀ достаточно знать пороговое приращение энергии (Δε)пop, связь которого с σ'₀ определяется формулами (2) и (6) при р=0,75 как

В работах, содержащих экспериментальные данные различения сигналов частоты 1000 Гц, длительностью 0,1 с, даны следующие величины (Δε)пор : 0,5 дб [14] и 0,7 дб [16] (В этих работах использовался метод вынужденного выбора в ситуации различения. Выбор именно этих данных объясняется следующими причинами. Оценки пороговых величин, приводимые в литературе, как уже отмечалось выше, являются проявлением не только сенсорных свойств наблюдателя, но также влиянием внесенсорных факторов, улавливаемых в колебаниях критерия в процессе эксперимента [1]. Это влияние в существенной мере определяется методикой эксперимента. Поэтому мы используем данные различения, полученные методом вынужденного выбора, в надежде, что загрубление оценок внесенсорными факторами в различении и в обнаружении при идентичной экспериментальной методике будет проявляться примерно в одинаковой мере, и оценка, по крайней мере, величины Δf будет близка к действительной. Можно было бы воспользоваться результатами экспериментов, проведенных по методу констант, являющемуся вариантом метода парных сравнений, однако, не говоря о принципиальных трудностях получения таким путем величины σ'₀, вызванных влиянием колебаний критерия наблюдателя, существенно меньших при использовании метода вынужденного выбора [1], следует указать, что достоверных данных по измерению дифференциальных порогов методом констант в литературе нет. Это объясняется тем, что начиная с Риза [21] в аналогичных измерениях использовался почти исключительно модуляционный метод [5], несопоставимый с методом констант). Выбрав среднее из них, имеем:

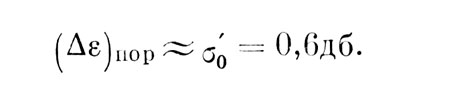
Исходя из универсальности выражения (3), вычисление величины Δf может быть произведено из уравнения, образованного приравниванием приращения энергии (Δε)пор для простого обнаружения определенной выше величине (Δε)пор. Таким образом, из уравнения (5) на пороге обнаружения имеем:

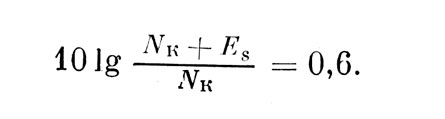
Откуда следует, что η_k-ε_s=8,2 (дб), где η_k=10 lg N_K/n₀, ε_S=10 lg Е_s/n₀.

Используем теперь данные по простому обнаружению, указанные белыми кружками на рис. 2; величине р=0,75 соответствует ε_s-η₀=10,5 дб. Сопоставляя это с последним выражением, имеем η_k=η₀+18,7; с другой стороны, согласно концепции критических полос η_k=η₀+10lgΔf. Следовательно, Δf=74.

Переходя к пьедестал-эксперименту, имеем

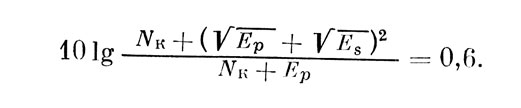
Используя данные пьедестал-эксперимента (ε_s-η₀=2,5 и ε_p-η₀=25) и его результаты, изображенные черными кружками на рис. 2, имеем Δf=73,3.

Таким образом, мы получили, что величины Δf, определенные из падежных экспериментальных данных с использованием предложенной нами теории, практически совпали для двух экспериментов разного рода (простое обнаружение и пьедестал-эксперимент), что свидетельствует об универсальности теории. Кроме того, полученный результат (Δf=74) поразительно близок к наиболее проверенным экспериментальным данным (Флетчер: 64 Гц, Хавкинс, Стивене: 79 Гц), и это позволяет положительно судить о правомерности теории.

Расчеты аналогичным нутом на других частотах с использованием данных, заимствованных из работ [11, 14], дали результат, сконцентрированный в таблице, третий столбец (Данные первой из цитируемых работ для 1000 Гц несколько отличаются от использованных нами ранее [8] и потому вычисленное значение Δf для 1000 Гц оказалось равным 69. Учитывая, однако, незначительность поправки, мы оставили в таблице величину 74 для лучшего согласования с контекстом). Нетрудно заметить, что теория одинаково хорошо работает на разных частотах.

3.5. Построение психометрических кривых. Определив, таким образом, параметры сг0 и Л/, мы можем построить, используя (4), психометрические кривые при 0≤Е_р<∞.

В частности, психометрическая кривая для простого обнаружения строится с помощью выражения (5) при σ₀=0,6 дб и 10 lg Δf=19 дб (сплошная кривая 1 на рис. 2; напомним, что штриховая кривая - предсказанная теорией идеального наблюдателя-психометрическая кривая). Психометрическая кривая для пьедестал-эксперимента при тех же σ₀ и Δf и при ε_р-η₀=25, рассчитанная с помощью (4), приведена па том же рисунке (кривая 2). Как видно из рис. 2, предложенная нами теория дает психометрические кривые, хорошо объясняющие экспериментальные данные как для простого, так и для пьедестал-эксперимента.

Если в качестве параметра рассматривать величину ε_р-η₀, то, используя формулу (4), при тех же σ₀ и Δf можно построить сеть психометрических кривых (рис. 6; направление стрелок указывает рост параметра, штриховая линия - предсказанная теорией идеальных наблюдателей кривая). Крайняя правая кривая на рис. 6а соответствует простому обнаружению (ε_р-η₀=-∞). При увеличении параметра кривые сдвигаются влево до тех пор, пока не будет выполнено равенство ε_р=η_к. Физически это вполне понятно; ведь добавление синусоидального сигнала в фазе к синусоидальному пьедесталу вызывает при достаточно малых уровнях пьедестала существенно большее приращение Δε, чем добавление того же сигнала к шуму. При дальнейшем росте параметра кривые смещаются вправо (рис. 66). Рост параметра, как и показывало проведенное ранее качественное исследование, сопровождается увеличением крутизны кривых до тех пор, пока величина N_K не окажется пренебрежимо мала по сравнению с Е_р. С этого момента, как это видно из рис. 66 и из анализа формулы (6), имеет место закон Вебера.

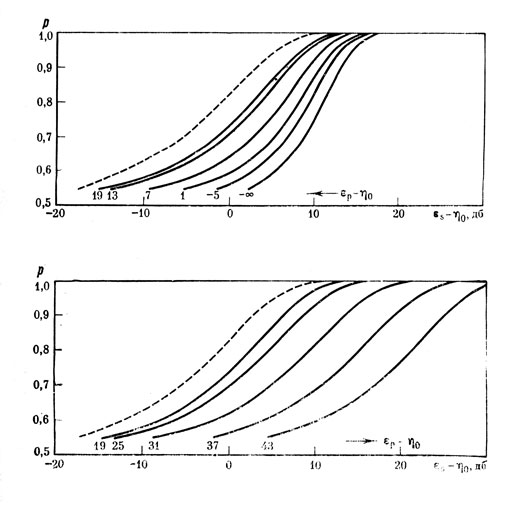
Рис. 6а и 6б

3.6. Снова о теории идеальных наблюдателей. Если теперь вернуться к теории идеальных наблюдателей, то становится ясным одно замечание Грина. Как мы уже упоминали, он утверждал, что психометрическая кривая для пьедестал-эксперимента по его данным оказывается сдвинутой на величину от 3 до 6 дб относительно теоретической; величина сдвига зависела от уровня пьедестала. Наша теория объясняет это наблюдение. Действительно, из рис. 6 видно, что результаты, указанные Грином, должны получаться при уровне пьедестала от 10 до 25 дб относительно спектральной плотности мощности шума; а при ε_р-η₀=19 дб экспериментальная кривая должна быть сдвинута относительно теоретической (штриховая линия) примерно на 3 дб. При других величинах ε_р сдвиг оказывается большим.

В литературе экспериментальные результаты, получаемые в пьедестал-эксперименте, иногда изображаются в виде зависимости р от уровня пьедестала (см. например, [14, 20]). Именно такая зависимость для любого уровня сигнала легко получается из рис. 6 при фиксировании некоторого значения ε_s-η₀(рис. 7; при ε_р-η₀=5 дб).

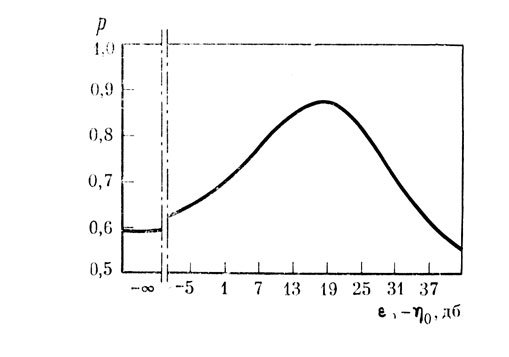
Рис. 7

В работе [20] сделана попытка объяснить такой экспериментально полученный ход кривой. За основу была взята наиболее правдоподобная энергетическая модель идеального наблюдателя, в которой для согласования с экспериментальными данными Грина, цитируемыми выше, была подобрана величина W, равная 1350 Гц. Это позволило объяснить восходящий участок кривой на рис. 7. При дальнейшем росте ε_р-η₀ энергетическая модель идеального наблюдателя давала, однако, монотонное возрастание кривой при асимптотическом приближении к горизонтали.

Чтобы объяснить экспериментально получаемый ниспадающий участок кривой, авторам пришлось вслед за Таннером [24] ввести в модель "внутренний шум", в результате чего модель при определенных условиях допускала закон Вебера. Не говоря уже о том, что концепция определенным образом меняющегося "внутреннего шума" не подтверждена, как указывалось выше, некоторыми экспериментальными результатами, обоснования требует также использование энергетической модели идеального наблюдателя для обнаружения тонального сигнала на фоне шума. Напомним, что эта модель была введена лишь для случая обнаружения шума на фоне шума [9,12]. Между прочим, в этой последней работе можно отметить аналогичное противоречие. Введя энергетическую модель для шумового сигнала (глава 6), авторы без всяких оговорок используют ее для ситуации обнаружения тонального сигнала на фоне шума (глава 8). Это, однако, не логическое упущение, а скорее сознательное замалчивание противоречий. Дело в том, что энергетическая модель идеального наблюдателя, в отличие от других моделей, предсказывает в простом обнаружении прямую пропорциональную зависимость d' и E_s, подтверждаемую экспериментальными данными.

3.7. Абсолютный и дифференциальный пороги. В теории обнаружения Светса и др. проводится четкая мысль об идентичности ситуаций обнаружения сигнала на фоне шума и абсолютного порога (понимаемого в операциональном смысле). Аналогия основывается на том, что в принципе безразлично, будет ли сигнал маскироваться внешним шумом или внутренним, так называемым сенсорным.

К сожалению, однако, эту теорию не удалось развить в область различения, и потому она не могла описать количественно чрезвычайно интересную область^ перехода от абсолютного порога к дифференциальному. Мы постараемся восполнить этот пробел в рамках энергетической етатистической теории.

В экспериментах по определению абсолютного и дифференциального порогов внешний источник шума отсутствует, и поэтому в (4) мы можем заменить N_K на N'_K, где N_K - приведенная спектральная плотность мощности внешнего шума, создающего тот же маскирующий эффект, что и внутренний шум. Под Е_р в (4) мы будем понимать энергию эталона.

Определим вид зависимости величины дифференциального порога от уровня эталона. Полагая, согласно (10), что Δε_пор=σ0, получим условие дифференциального порога 1+(√x+√у)²/1+x=c, где x'=E_p/N'_к, у=E_s/N'_к, с определяется из соотношения σ₀=10lg с. Путем элементарных преобразований получаем выражение

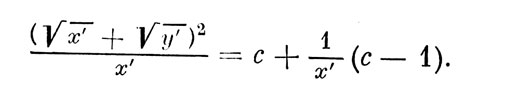
Учитывая, что левая часть последнего выражения - отношение энергий на пороге, получаем зависимость величины дифференциального порога от энергии эталона

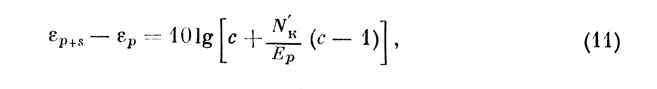
где ε_P+S - уровень эталон + переменный стимул.

Из (11) видно, что при Ер -> ∞ величина дифференциального порога стремится к константе 10lgс=σ₀, что является констатацией закона Вебера.

При Ер -> 0 выражение (11) должно дать величину абсолютного порога; таким образом,

Получившуюся в правой части величину назовем уровнем абсолютного порога ε_а. Тогда энергия абсолютного порога Е_a определиться как Е_а=N'_к(с-1).

Подставив полученное выражение в (11), имеем

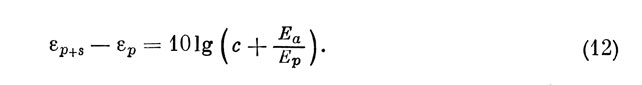
Формула (12) дает возможность вычислить абсолютный порог, используя величину дифференциального порога при малых уровнях, причем без всяких ограничений на форму сигнальной функции.

В частности, при Е_р=Е_а, т. е. при определении первого дифференциального порога, когда эталоном служит абсолютный порог, имеем: ε_a+s-ε_a=10 lg (1 + с).

При σ₀->0 величина с->1, ε_a+s-εa=3 дб и, таким образом, первый дифференциальный порог равен абсолютному.

При относительно малых σ₀ величина с близка к единице (при σ₀=0,6 дб, например, с=1,15 и ε_a+s-ε_a=3,3 дб), так что, получив дифференциальный порог, равный 3 дб, мы можем считать бее большой ошибки, что эталон был равен абсолютному порогу. Если же ориентировочное значение σ₀ велико, то для точного определения абсолютного порога нужно учитывать величину с, определив σ₀ или, что то же самое, - установившееся значение дифференциального порога.

Можно, конечно, решать и обратную задачу: по величине дифференциального порога в данной стимульной точке и по σ₀ определять величину 10 lg E_a/E_p, дающую в дб расстояние абсолютного порога от этой стимульной точки.

Таким образом, проблема измерения абсолютного порога подменяется, с помощью нашей модели, проблемой дифференциальных порогов, решаемой существенно проще.

В качестве примера приведем экспериментальные данные Миллера [17] для двух наблюдателей при использовании шумового сигнала (рис. 8) в виде зависимости величины дифференциального порога от уровня эталона (ε_р) над уровнем абсолютного порога (ε_а); величину последнего Миллер взял из литературных источников.

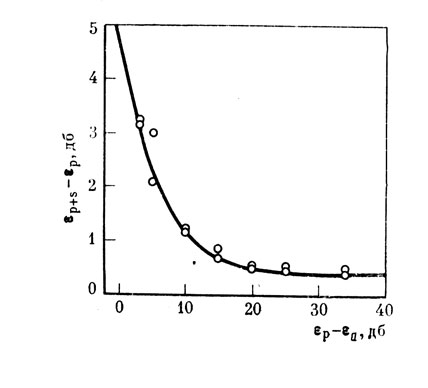
Рис. 8

Наши вычисления, однако, показывают, что подобная зависимость могла получиться в эксперименте Миллера при абсолютном пороге на 3 дб более высоком. В этом предположении, согласно (12), была построена теоретическая зависимость (кривая на рис. 8), которая достаточно хорошо аппроксимирует ^экспериментальные данные.

Выводы. Использование математического аппарата статистической радиотехники в психофизике, реализованное теорией идеальных наблюдателей, нельзя считать оправданным полученными результатами.

Энергетическая статистическая теория, построенная на базе классических психофизических законов Вебера, Фех-нера, Терстона и использующая свойства слухового анализатора, позволила объяснить многочисленные экспериментальные данные, в том числе и те, которые были получены в рамках теории идеальных наблюдателей.

Энергетическая статистическая теория дает единообразное описание ситуаций обнаружения, различения и абсолютного порога.