2. Теория идеальных наблюдений

В основу теории (наиболее полно она изложена в монографии [12]) положено представление о том, что статистический характер ощущения на сенсорной оси R (рис. 1) определен случайным изменением некоторого параметра, связанного исключительно со статистическим характером шума. Наблюдатель представляется в виде радиотехнического устройства, сравнивающего величины указанного параметра и дающего на выходе результат этого сравнения (Таким образом, в этой теории неявно постулируется линейность преобразования физической оси в сенсорную). Характер параметра определяется спецификой условий обнаружения, точнее, спецификой информации, которую имеет идеальный наблюдатель относительно сигнала. Выделение параметра осуществляется путем определенного рода представления шумовой и сигнальной функций.

Пусть n (t) - функция, описывающая шум. Как всякую непрерывную функцию времени, ее можно аппроксимировать дискретной последовательностью из 2WT импульсов, где W - ширина спектра шума, Т - длительность, с временным интервалом между импульсами, равным Δt, Δt=1/(2W). Каждый из 2WT импульсов имеет амплитуду x_i/i=1, 2, ,..., 2WT/, равную значению функции на временном интервале t_i= i/(2W), так что x_i=n(t_i). Если шум - гауссов, то величины x_i распределены по нормальному закону со средним, равным нулю и с дисперсией N₀W, где N₀ - мощность шума в полосе 1 Гц (спектральная плотность мощности шума). Сигнальная функция s (t) представляется в этой теории аналогично, в виде последовательности из 2WT импульсов.

Форма сигнала может быть точно определена, например, известно, что это - синусоидальный сигнал определенной амплитуды, частоты и начальной фазы. Тогда сигнал s (t) может быть точно известен наблюдателю в следующем смысле: используя временное представление сигнала в виде 2WT импульсов, наблюдатель знает, что если сигнал послан, он будет иметь определенные значения s_i=s(i/2W), i=1, 2,..., 2WT на каждом временном интервале. Предполагается, что наблюдатель способен использовать корреляцию между ожидаемым и принятым в смеси с шумом сигналом. В этом случае реализуется модель идеального наблюдателя для сигнала, определенного точно, с помощью которой мера сенсорной чувствительности d' выражается следующим образом:

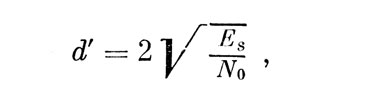
где E_s - энергия сигнала.

Если сигнал определен статистически, например, определенной частоты и амплитуды, но неизвестной начальной фазы, то вводится модель идеального наблюдателя для обнаружения по огибающей. В этом случае используется представление шума и сигнала в виде разложения по конечным рядам Фурье с 2WT коэффициентами (В ранних работах Петсрсона, Бсрдсала, Фокса [19] этот математический аппарат использовался и для первой модели, т. е. в случае сигнала, определенного точно). Величину d' в этой модели заменяет параметр А, равный отношению амплитуды сигнала к среднеквадратичному напряжению шума.

Сигналом может быть один из М ортогональных (Термин "ортогональный" имеет математический смысл и введен авторами теории для удобства формализации; дать ему физическое толкование, по-видимому, невозможно) сигналов, причем число М - известно наблюдателю. В этом случае теория дает выражение для d', в которое М входит как параметр.

И, наконец, сигналом может быть просто полоса шума. Если такой "сигнал добавляется к маскирующему шуму, то общая мощность возрастает; этот случай описывает энергетическая модель идеального наблюдателя. При некоторых допущениях теория дает следующее выражение для d':

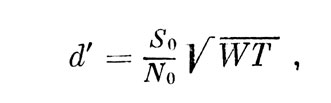
где S₀ - мощность шумового сигнала в полосе 1 Гц.

Шумовой сигнал, в представлении авторов теории, является нижним пределом в континууме возможных сигналов разной степени неопределенности. Наблюдателю неизвестны ни частота, ни фаза, ни какие-нибудь другие характеристики сигнальной функции. Для выбора типа ответа используется лишь энергетический параметр сигнала.

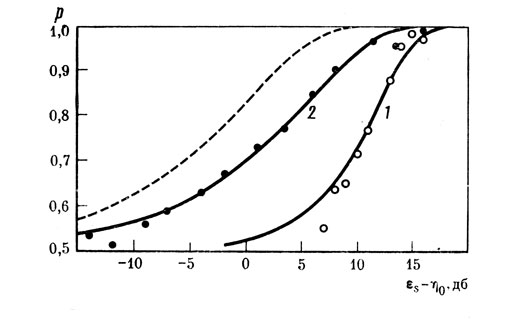
Рис. 2

Из сказанного следует, что теория предлагает не одного идеального наблюдателя, а несколько. Прилагательное "идеальный" относится к потенциально наилучшим характеристикам наблюдателя в тех или иных условиях. Каждая ситуация обнаружения, которая характеризуется определенной степенью знания наблюдателем параметров сигнала, требует особого идеального наблюдателя, чтобы достигнуть оптимальных условий обнаружения.

В упоминавшейся монографии Грина и Светса [12], на основе проведенных ранее "базовых" экспериментов [8], названных так, очевидно, потому, что результаты этих экспериментов более всего приближались к теоретическим предсказаниям, дано сравнение идеального и натурального наблюдателей при использовании метода вынужденного выбора. Соответствующие зависимости относительного числа правильных ответов от уровня сигнала (психометрическая кривая) приведены на рис. 2; теоретическая - для сигнала, определенного точно (штриховая линия), экспериментальные точки (светлые кружки) получены при η₀=10 lg (N₀/n₀)=40 дб (n₀=0,0002 дн/см²), частоте сигнала f_s=1000Гц, длительности 0,1 с. Приведенные зависимости позволят проверить предсказания теории в двух аспектах: по форме психометрической кривой и по порогу обнаружения (последний вводится как понятие операциональное, обозначающее уровень сигнала относительно шума, при котором достигается 75% правильных ответов). Из рисунка видно, что расхождение между теоретической кривой и кривой, которой можно аппроксимировать экспериментальные точки, весьма велико как по крутизне кривых, так и по величине порога (последнее - примерно равно 13 дб). Различие в крутизне кривых и в величине порога объясняют следующим образом.

Если допустить, что идеальный наблюдатель не улчет точно природу сигнала, то теория дает целый класс теоретических психометрических кривых; каждая из этих кривых характеризует работу наблюдателя при условии, что сигналом будет один из М (М - параметр кривых) ортогональных сигналов, и это известно наблюдателю. Если сигнал известен точно, то М=1 и неопределенности нет. Если неопределенность, характеризуемая увеличением числа М, возрастает, то крутизна психометрических кривых увеличивается. Теоретический порог обнаружения также несколько увеличивается, однако расхождение теоретических и экспериментальных данных все же остается значительным [8, 12].

Некоторые экспериментальные процедуры, призванные уменьшить неопределенность наблюдателя относительно параметров сигнала различными косвенными путями, имели лишь частичный успех [8]. Подтверждение своих выводов авторы теории нашли в экспериментах, в которых попытка уменьшить неопределенность относительно параметров сигнала привела к изменению задачи обнаружения таким образом, что наблюдатель получал прямую информацию о сигнале. Чтобы исключить неопределенность относительно частоты сигнала, например, можно добавлять к шуму непрерывный синусоидальный сигнал на таком уровне, чтобы он легко был заметен па фоне шума. Подлежащий обнаружению сигнал тогда представляет собой синусоидальный короткий сигнал той же частоты, добавляемый к непрерывной синусоиде и вызывающий приращение уровня синусоидального сигнала, заметить которое - задача наблюдателя.

Эта процедура, однако, не исключает неопределенности относительно начала сигнала. Та же процедура, которая, по мнению Грина, минимизирует практически все виды неопределенности, представляет собой, в действительности, модификацию эксперимента по определению дифференциального порога для интенсивности. Она заключается в том, что на фоне шума наблюдателю предъявляются две синусоиды одинаковой длительности: одна - на стандартном уровне (пьедестал), другая - на несколько более высоком уровне, образованном за счет прибавления к пьедесталу сигнала той же частоты и фазы. Задача наблюдателя - определить интервал, содержащий сигнал.

Результаты "базового" пьедестал-эксперимента, заимствованные из работы [12] со ссылкой на работу [8], представлены на рис. 2 (черные кружки). Экспериментальные условия: η₀=40 дб, f_р=f_s= 1000 Гц, длительность 0,1 с, ε_р-η₀=25 дб, где ε_p и f_р - соответственно, уровень и частота пьедестала. Если сравнить приведенные на рис. 2 экспериментальные данные, то нетрудно заметить, что кривая, которой можно аппроксимировать экспериментальные данные для пьедестал-эксперимента, стала более пологой, чем соответствующая кривая для простого обнаружения. Психометрическая кривая для пьедестал-эксперимента оказалась действительно параллельной теоретической для случая сигнала, известного точно. По утверждению Грина [8], психометрическая кривая оказывается сдвинутой вправо от теоретической на величину от 3 до 6 дб, в зависимости от энергии стандартного синусоидального сигнала (пьедестала). Это расхождение объяснялось просто как естественное отличие идеального от наблюдаемого.

Показав таким образом, что ответы реального наблюдателя в условиях пьедестал-эксперимента описываются кривой, близкой по форме теоретической для сигнала, известного точно, исследователи столкнулись с очередной неприятностью. Оказалось, что при увеличении амплитуды пьедестала уровень сигнала, необходимый для получения того же относительного числа правильных oтветов, также возрастает [24, 14]. Психометрическая кривая, сохраняя свою форму, смещается вправо по мере увеличения амплитуды сигнала и пьедестала. При этом отношение амплитуд сигнала и пьедестала, необходимое для данного относительного числа правильных ответов, естественно, оказывается постоянным; этот эмпирический факт описывается законом Вебера. Однако ни одна из моделей идеального наблюдателя в приложении к пьедестал-эксперименту не смогла согласоваться с законом Вебера [12]. Было произведено несколько попыток усовершенствовать модель идеального наблюдателя, допуская наличие "внутреннего шума", пропорционального среднему уровню внешнего шума в сумме с пьедесталом [20, 24], однако они дали лишь удовлетворительное качественное описание экспериментальных результатов и, кроме того, не согласовывались с последующими экспериментами [15].

Мы остановились лишь па основных положениях теории идеальных наблюдателей и убедились в том, что в отношении предсказания экспериментальных результатов она особого успеха не имела. Действительно, результаты простого эксперимента по обнаружению теорией предсказываются плохо как по форме психометрической кривой, так и по величине порога обнаружения; переход к пьедестал-эксперименту позволил получить психометрическую кривую, по форме близкую к теоретической, однако в отношении величины порога обнаружения вопрос остался открытым. Кроме того, выводы теории в приложении к пьедестал-эксперименту противоречат закону Вебера.

Таким образом, использование математического аппарата статистической радиотехники, осуществленное теорией идеальных наблюдателей, не дало, но нашему мнению, положительных результатов.