§ 2. Методика

А. Планы экспериментов

а) Основной план. Экспериментальное изучение переноса требует, чтобы опыты проводились в соответствии с определенным планом. Фолькман (1858) был первым, кто предложил адекватную методику.

Основной принцип заключается в том, чтобы можно было с уверенностью утверждать, что изменение эффективности выполнения второй задачи является результатом предшествующей деятельности. Необходимо, таким образом, сравнивать эффективность при наличии и отсутствии первой задачи.

Основной план, который может существовать в различных вариантах, состоит в следующем.

Пусть В - задача, на которой изучается явление переноса, и А - задача, вызывающая этот эффект. Эксперимент должен быть построен таким образом, чтобы оказалось возможным сравнить результаты экспериментальной группы Е с результатами контрольной группы С (ВЕ и Вс - результаты этих групп при выполнении задачи В). Эти группы, которые обязательно должны быть эквивалентными, выполняют задачи А и В по следующей схеме:

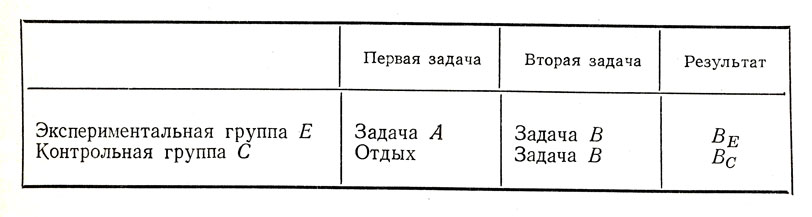
Сравнение результатов позволяет утверждать, что, если В_Е>В_С, эффект переноса положителен - имеет место проактивное облегчение. Если В_Е=В_С, эффект переноса равен нулю. Если В_Е<В_С, эффект переноса отрицателен - имеет место интерференция или проактивное торможение.

Такой план эксперимента позволяет изучить влияние задачи А в целом. Если же нас интересует роль какой-нибудь одной из переменных задачи А, необходимо составить столько экспериментальных групп, сколько существует вариантов изменения этой переменной.

В случае трех модификаций задачи А - А₁, А₂ и А₃ - план будет выглядеть следующим образом:

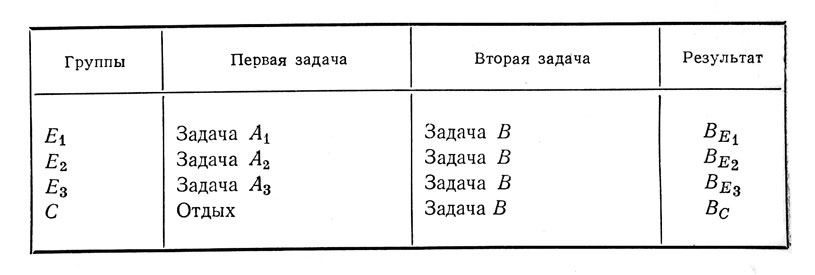
Сопоставление результатов различных групп - Е₁, Е₂ и Е₃ - позволяет выявить, как сказывается на переносе влияние данной переменной. Контрольная группа дает возможность уточнить направление и величину переноса.

б) Реализация вышеописанного плана связана, однако, с двумя трудностями. 1) Прежде всего необходимо, чтобы экспериментальные и контрольная группы были эквивалентными в отношении способности выполнить задачу В. Чтобы преодолеть эту трудность, можно предложить испытуемым выполнить задачу, аналогичную задаче В, после чего разделить их на основании полученных результатов на две эквивалентные группы - Е и С.

Задача Р, аналогичная задаче В, может, особенно если выполнение ее требует длительного времени, вызвать перенос. Можно, конечно, предположить, что, поскольку группы Е и С эквивалентны, проактивный эффект задачи Р проявится в них в одинаковой мере. Единственная сложность связана с тем, что в группе Е проактивный эффект задачи Р скажется сначала на выполнении задачи А, а затем задачи В; в группе С, напротив, влияние задачи Р отразится непосредственно на выполнении задачи В.

Необходимо, таким образом, свести к минимуму этот проактивный эффект, сделав предварительное испытание как можно более коротким и отодвинув его от основного эксперимента на достаточно продолжительный период времени.

2) Вторая, уже упомянутая нами трудность связана с эффектом "включения в работу", который не одинаковым образом проявляется на уровне задачи В в экспериментальной и контрольной группах. Существование этого феномена было хорошо показано в опытах Хэмилтона (1950). Исследователь систематически менял продолжительность интервала между двумя эквивалентными научениями. Последние сводились к заучиванию списка пар ассоциированных слов (число - прилагательное). Продолжительность интервала между двумя последовательными научениями принимала следующие значения: 10, 20, 40, 60, 120, 180 и 240 минут. Как показывает график на рис. 16 (стр. 200), эффективность заучивания во второй задаче убывает обратно пропорционально продолжительности интервала.

Чтобы компенсировать эффект включения в работу, можно предложить контрольной группе выполнить во время периода отдыха нейтральную задачу X, индифферентную по отношению к изучаемым переменным, то есть никак не связанную ни с задачей Л, ни с задачей В. В этом случае можно предполагать, что выполнение нейтральной задачи окажет на группу С действие, тождественное эффекту включения в работу, не вызвав, однако, при этом проактивных эффектов. Как подчеркивает Тьюн (1951), соблюсти эти условия очень трудно.

Можно сравнить влияние задачи X с эффектом мнимого отдыха - испытуемый фактически никогда не бывает совершенно бездеятельным, как правило, он занят выполнением более или менее явных, но, безусловно, трудно поддающихся контролю задач (Осгуд, 1953; Мёр док, 1957).

В таком случае план эксперимента имеет следующий вид:

Сопоставление групп С и С' позволяет выявить эффект "включения в работу".

в) Сопоставление эффектов переноса. Среди проблем, возникающих при изучении переноса, одной из наиболее частых является следующая: одинаковы ли эффекты переноса при переходе от задачи А к задачам В и В'; оказывается, можно сравнить между собой задачи В и В' по одной переменной, которая и становится объектом изучения. Цитировавшийся выше эксперимент Мартина (1915) является хорошей иллюстрацией этой проблемы.

Итак, мы получаем следующий план эксперимента, если, разумеется, не будем принимать во внимание описанные выше вторичные эффекты:

На основании результатов контрольных групп становится возможным получить и сравнить между собой значения переноса при переходе от выполнения задачи А к задачам В и В'.

г) Обратимость эффекта переноса. Еще одна часто возникающая проблема состоит в том, чтобы узнать, является ли эффект переноса в случае задач А и В реципрокным.

Эта довольно простая проблема возникает всякий раз, когда испытуемый должен последовательно выполнить две не связанные между собой задачи, и нас интересует при этом, какая из них наилучшим образом способствует выполнению последующей. Чтобы получить ответ на этот вопрос, достаточно осуществить такой план, предусматривающий уравновешивание экспериментальных ситуаций:

В этом случае каждая из экспериментальных групп Е₁ и Е₂ выступает в качестве контрольной по отношению к другой.

Таким способом Эндрис, Грин и Спраг (1954) смогли показать нереципрокный характер эффекта переноса в случае двух задач, в которых испытуемый должен был совмещать с помощью ручного управления светящуюся мишень и подвижную точку. В одной из них надо было совмещать точку с подвижной мишенью, во второй - удерживать смещающуюся точку на поверхности неподвижной мишени.

Реципрокность эффекта переноса не наблюдалась также в случае двух задач на распределение карт; в первой задаче карты были окрашены в голубой, красный, зеленый и желтый цвета, во второй - на карты были нанесены символические изображения. Причем последние были напечатаны таким образом, что трудно было определить, где верх, где низ, где лицевая и где оборотная сторона карт. Было установлено, что при переходе от распределения карт с символами к распределению цветных карт эффект переноса выражен более сильно, чем при обратном переходе. Распределение символов предполагает, таким образом, процессы хотя и достаточно элементарные (различение V, Т, Z, D), однако более сложные, чем процессы, связанные с различением цветов, которые еще более примитивны.

д) Перенос и повторное научение. Явление переноса изучается не только в ситуации выполнения второй задачи, но также и в условиях повторного научения. Нетрудно - на основании предыдущих планов - получить следующий план исследования:

В этом плане учитывается также отсрочка вс времени повторногб научения, эффект которой может проявиться независимо от эффектов, связанных с первичным научением выполнению задачи В (группа d).

Сравнение результатов выполнения задачи В различными группами позволяет без большого труда выявить не только эффект переноса, но и эффекты забывания и реминисценции.

Мы видим, таким образом, что с помощью перечисленных выше планов экспериментов можно изучать влияние различных переменных как задачи В, при выполнении которой проявляется эффект переноса, так и задачи А, с которой связано происхождение этого эффекта. Нетрудно также убедиться в важности учета при разработке общего плана эксперимента таких временных факторов, как продолжительность выполнения задач (и главным образом первой) и длительность интервала между их выполнением. С проявлениями этих факторов нам предстоит познакомиться позднее.

Б. Мера переноса

Мёрдок (1957) подчеркивает, насколько важно найти адекватную и, следовательно, эффективную меру переноса, чтобы можно было перейти от описания явлений к установлению общих закономерностей. Проблема эта, однако, сложна, поскольку показатель, с помощью которого будет оцениваться величина переноса, не должен зависеть от единиц измерения, используемых в данном эксперименте (секунд или минут, в которых измеряется время, необходимое для выполнения задачи; числа успешных проб и т. д.).

Чаще всего перенос оценивается в процентах, так как эта величина не зависит от единицы, используемой при конкретном измерении.

Понятие величины переноса предполагает наличие связи между результатами двух групп - контрольной и экспериментальной. Это, таким образом, сравнительная мера. Ее простейшая формула впервые была предложена Ганье, Форстером и Краули (1948).

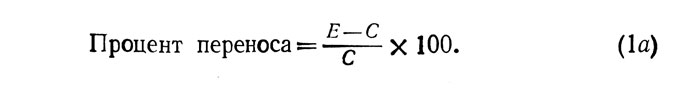
Эта формула особенно удобна в тех случаях, когда положительный эффект переноса выражается в увеличении количества единиц, на основании которых подводится итог (количества успешных попыток, например).

Если же дело касается уменьшения количества ошибок или длительности выполнения задачи, что также является проявлением положительного переноса, формула приобретает следующий вид:

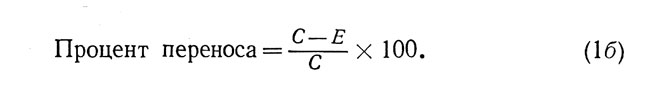
Эта формула, однако, не является вполне удовлетворительной, поскольку максимальное значение переноса в процентах, выраженное таким образом, будет стремиться к бесконечности, когда Е>С. Напротив, результат окажется равным нулю, когда эффективность деятельности обеих групп будет одинаковой: С=Е. Эта формула верна только в случае отрицательного переноса, эффект которого может меняться от 0 до -100%.

Ганье и другие (1948) сами подвергли критике эту формулу. Поскольку в большинстве случаев явление переноса изучается с целью выявления положительного эффекта, ими была предложена новая формула, в которой максимальному положительному переносу соответствует 100%. И напротив, максимальный отрицательный эффект соответствует бесконечности (-∞). Вот эта формула:

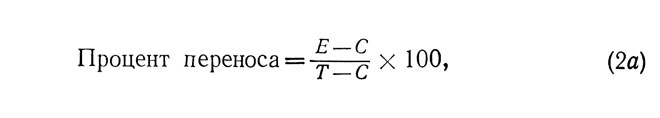
если подсчитываются правильные ответы, и

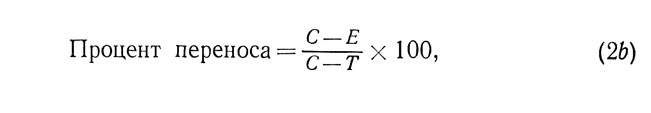
если подсчитываются ошибки.

В формуле (2а) буквой Т обозначается максимальное число правильных ответов, ожидаемое при выполнении данной задачи. Это число может быть теоретическим, если a priori известно возможное число правильных ответов (число усвоенных слов, количество подлежащих установлению связей между стимулами - сигналами - и двигательными реакциями). Но это число может быть также получено опытным путем, если теоретические границы нельзя определить с помощью дедукции. Так обстоит, например, дело в случае очень сложных и практически невыполнимых задач.

В формуле (2b) буквой Т обозначается минимальное число ошибок.

Мёрдок (1957) отмечает, что и формула (2а), и формула (2b) позволяют получить процентное выражение переноса, представляющее собой одновременно функцию результатов контрольной и экспериментальной групп, и что величина переноса зависит, в частности, от расхождения между результатом контрольной группы и возможным максимальным результатом Т. Если эта разница слишком велика, то значения Е должны быть весьма значительными по сравнению с С, для того чтобы процент переноса был высоким.

Как мы уже указывали, эта формула несимметрично описывает эффекты положительного и отрицательного переноса.

Для того чтобы устранить это неудобство, Мёрдок предлагает следующие формулы:

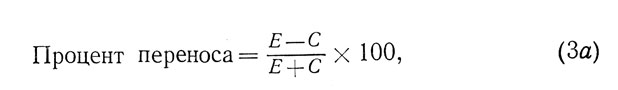
где Е и С обозначают правильные ответы, и

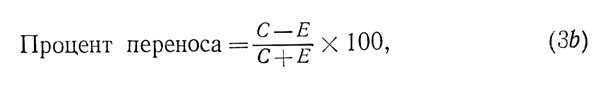
где E и С обозначают ошибки.

Эти формулы позволяют, во-первых, охватить диапазон от -100 до +100% и, во-вторых, обойтись без подсчета максимального числа правильных ответов или ошибок в каждом конкретном случае.

Значения переноса, полученные с помощью трех приведенных выше формул, представлены в следующей таблице.

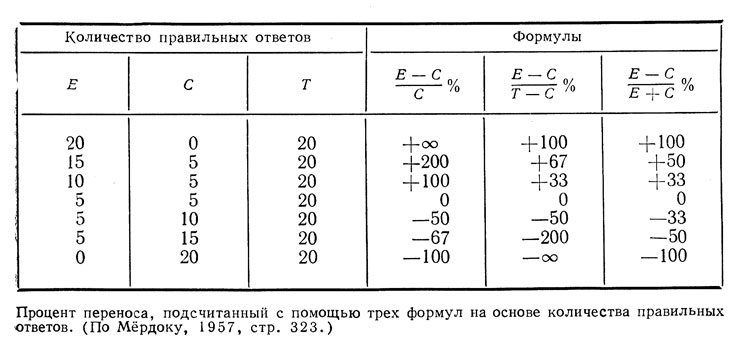
Таблица III

В. Проявления эффекта переноса на кривой научения

Чаще всего эффект переноса наблюдается при сопоставлении результатов двух испытаний в ходе научения, и именно сравнение кривых научения позволяет нам убедиться в его существовании.

Можно, конечно, изучать перенос, установив для обеих задач некоторый критерий успешности и учитывая только количество проб, необходимых для его достижения. Таким образом, оказывается возможным использовать одну из формул, представленных в предыдущем параграфе.

Можно также сравнивать проба за пробой количество правильных ответов на протяжении каждого из двух периодов научения. Различные значения, получаемые в каждой пробе, позволяют проследить эволюцию переноса.

Нужно отметить, что эффект переноса может проявляться как в изменении формы кривой научения, так и в изменении конечного числа правильных ответов. Вудвортс и Шлосберг (1954) продемонстрировали этот факт, оценивая изменение нормы совершенствования навыка как функцию угла наклона кривой.

На рис. 2 представлены результаты контрольной и экспериментальной групп.

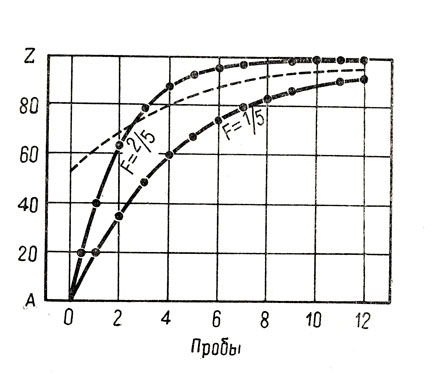
Рис. 2. Возможные проявления переноса на кривой научения. Кривая, обозначенная F=1/5, отражает прогресс контрольной группы. Кривая, обозначенная F=2/5, предполагает, что скорость научения увеличивается вдвое в результате некоторого предварительного научения: она начинается на том же исходном уровне, но достигает конечного уровня в два раза быстрее. Штриховая линия показывает, что в случае экспериментальной группы расстояние по вертикали, которое должна пройти кривая научения, чтобы достичь конечного уровня, уже с самого начала сокращается вдвое вследствие предварительного упражнения (по сравнению с контрольной группой), несмотря на то, что F сохраняет значение 1/5. Сравнение с теоретической кривой показывает, что штриховая кривая достигает каждого уровня на 3,1 пробы раньше. Иными словами, число проб экспериментальной группы составляет 44% от числа проб контрольной (по Вудвортсу и Шлосбергу, 1954, стр. 738)

Уравнение научения имеет следующий вид:

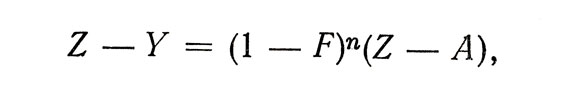
где Z - практически достижимый уровень выполнения задачи; А - исходный уровень; Z-А -диапазон возможного совершенствования; F - темп совершенствования.

В рассматриваемом примере F=1/5 для контрольной группы и 2/5 - для экспериментальной группы. Величина переноса, таким образом, составляет 44%.