Построение структурных моделей деятельности путем априорной алгоритмизации (Г. В. Суходольский)

При проектировании систем "человек-техника" все большее распространение приобретают методы построения структурных моделей деятельности путем априорной алгоритмизации. Под априорной алгоритмизацией деятельности специалиста будем понимать процесс последовательного анализа и синтеза иерархической системы целей (задач), возникающих перед специалистом, условий их возникновения (режимов работы) и правил поведения (алгоритмов), приводящих в заданных условиях к достижению определенной цели. Методы априорной алгоритмизации в основном изложены в [1]. Однако вопрос о получении оценок для взвешивания частных алгоритмов и о способах синтеза более крупных структур из подструктур, описываемых на уровне частных алгоритмов, разработан недостаточно. Субъективные методы ранговых оценок частоты и важности использования специалистом средств контроля и управления а также связей между ними, предложенные в ряде работ (на-пример [2]), непригодны из-за неадекватности субъективных оценок в случае значительного числа средств контроля и управления (более десяти). В данной работе излагается один практический способ построения операционно-логических и предметно-функциональных структурных моделей деятельности специалиста^*.

^* (Понятия OЛ- и ПФ-моделей деятельности в общем виде рассмотрены в статье: Суходольский Г. В. Абстрактная модель деятельности специалиста и ее реализации. - Вестн. Ленингр. ун-та, 1972, № 11, с. 92-95.)

Пусть в терминах, используемых при автоматизации объектов управления, определены l задач и m режимов работы специалиста, причем в силу некоторой энтропии ситуации решение i-й задачи (i=1,2, ..., 1) в r-ом режиме (r=1,2, ..., га) возможно n способами, так что i-й способ (i=1,2, n) выбирается специалистом смотря по обстоятельствам, либо из числа заученных в предыдущей профессиональной жизни, либо благодаря эвристической деятельности. Иначе говоря, i-ая задача решается специалистом по гибкому алгоритму, каждая реализация которого есть конечная жесткая последовательность сенсорных, моторных и логических операций, имеющая частоту f_rij и матрицу смежности операций A_rij.

Перечисляя реализации гибкого алгоритма i-й задачи, можно установить полное множество всех сенсорных, моторных и логических операций, необходимых и достаточных, согласно имеющейся априорной информации, для решения специалистом i-й задачи. Это множество образует столбцы и строки матрицы i-ro алгоритма в r-ом режиме (B_ri). Если матрицу A_rij рассматривать как реализацию матрицы B_ri то, очевидно,

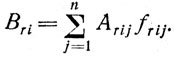
Аналогично получаем матрицу C_r для r-го режима работы специалиста:

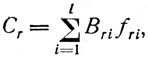
где f_ri - частота реализации Bri в матрице C_r, а также матрицу D, эквивалентную ОЛ-модели деятельности при всех m режимах:

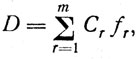
где f_r - частота r-го режима работы, Обобщая (1), (2) и (3), получаем аддитивную модель для синтеза целостной деятельности из "элементарных" алгоритмов:

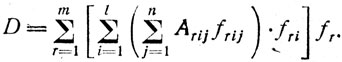
Рассмотрим на примере некоторые существенные детали предлагаемого подхода.

Пусть имеется система управления, состоящая из объекта и специалиста (ниже приведена спецификация параметров алгоритма задачи):

Для простоты ограничимся априорной алгоритмизацией задачи "изменить выход продукта на заданную величину".

В распространенной записи алгоритм этой задачи в аналитической форме имеет вид:

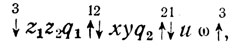
где z₁, z₂, x, y, u - текущие значения параметров,

q₁=0 - объект неисправен,

q₁=1 - объект исправен,

q₂ - заданное изменение y достигнуто,

q₂ - заданное изменение y не достигнуто,

ω=0 - логические операторы, организующие управление. Форма (5); не дает, однако, сведений ни о частоте реализаций алгоритма (f_j), ни об их количестве. Один из возможных способов получения таких сведений основывается на том очевидном обстоятельстве, что частота оператора есть функция исходов опыта. Но исходы опыта можно перечислить и априорно как возможные реализации формы (5), получаемые по комбинациям значений логических условий:

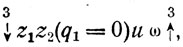
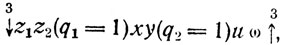
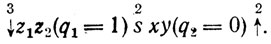
Заметим, что последняя реализация (5.3)* не определена, так как заканчивается циклом

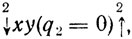
из которого не указано правило "выхода". 82

Очевидно, любой цикл для устойчивого регулятора должен иметь конечную, причем небольшую по величине, степень. Для человека в подобных задачах, как показали теоретические выкладки А. И. Губинского и данные эксперимента [3, 4], вероятность повторения такого цикла ровно k раз, после чего реализуется (5.2), подчиняется геометрическому распределению

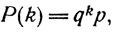
параметры q и p которого зависят от обстоятельств. На основании обобщения опытных данных можно принять оценки вероятностей P(k), представленные в табл. 1. Можно видеть, что с вероятностью P [k≤4]=0,87 реализуются варианты алгоритма (5), включающие циклы со степенями k=0÷4. Тогда, рассматривая реализацию (5.2) как имеющую этот цикл в нулевой степени, можем перечислить дополнительно четыре реализации:

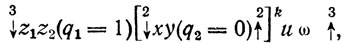
где степень цикла изображена в виде показателя степени у квадратных скобок, заключающих символическую запись цикла.

Таблица 1. Статистические характеристики цикла k-й степени

Таким образом, с достаточной вероятностью возможны пять реализаций гибкого алгоритма (5), описывающие управление при неисправности объекта.

Для получения ОЛ-модели на уровне отдельного гибкого алгоритма, согласно уравнению (1), необходимо построить матрицу смежности вершин. Так как в алгоритме (5) всего восемь вершин (семь операций, за восьмую вершину принимается внешняя среда), то матрица A_j имеет порядок 8 и содержит 56 элементов. Нетрудно, однако, видеть, что только 9 из них отличны от нуля, т. е. дуги связывают, как устанавливается по реализациям (5.1) - (5.6), только девять пар вершин. В целях экономии можно поступить следующим образом.

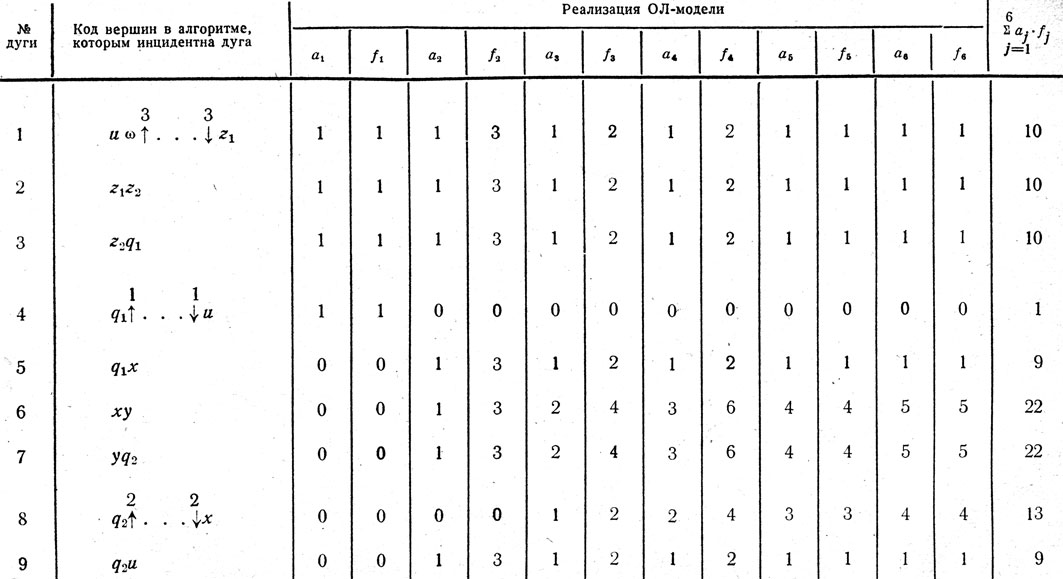
Таблица 2. Сокращенный табличный способ синтеза OЛ-модели по реализациям алгоритма задачи

По реализациям алгоритма выписываются пары вершин (в кодах операций алгоритма), в первой из которых начинается, а во второй кончается дуга ненулевой частоты. Далее, как это сделано в табл. 2, реализации алгоритма записываются в виде векторов-столбцов (или строк), элементы которых суть дуги либо с невзвешенной частотой a_j, либо со взвешенной частотой f_j=k+2, значения которой приведены в табл. 1 (при j=1 примем f_j= 1, так, чтобы Σ_j=1f_j=k+2=10). Из табл. 2 нетрудно видеть, что для каждой реализации первый столбец a_j умножается на второй столбец f_j, после чего результаты складываются. Таким образом, в последнем столбце получаются элементы матрицы B_i смежности вершин орграфа ОЛ-модели для алгоритма (5), по которым легко записать эту матрицу в обычном, полном виде.

Заметим, что в моделях (1)÷(3) для каждой вершины сумма "входящих" дуг должна быть равна сумме дуг "исходящих", это правило выполнено для реализаций, записанных в табл. 3, и служит для проверки правильности построения моделей.

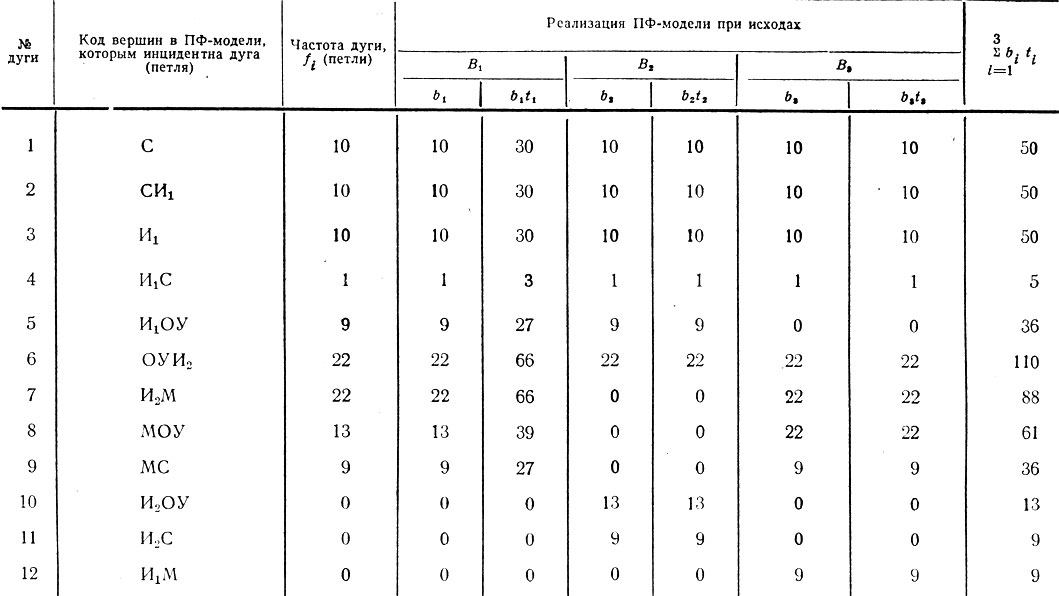
Таблица 3. Сокращенный табличный способ синтеза ПФ-модели по трем ее реализациям

Переход к ПФ-модели состоит в том, что сенсорные, моторные и логические операторы "материализуются" в средства контроля и управления. Так, в рассматриваемом примере для операций z₁ и u, средства получения команд и докладов можно объединить в селекторе (С). Пусть состояние исправности объекта сигнализируется индикатором И₁ значения y - индикатором И₂, а значения x изменяются органом управления ОУ. Тогда логический оператор q₁ "поглощается" индикатором И₁, а q₂ "материализуется" в виде мнемоники М - списка значений x, соответствующих требуемым уровням y.

Собственно преобразование ОЛ-графа в ПФ-граф состоит в том, что множество вершин, изображающих средства контроля и управления, на схеме соединяется дугами в соответствии с исходным ОЛ-графом. Менее наглядно эта процедура выполняется в полной или сокращенной матричной форме, например, как показано в табл. 3, где в трех первых столбцах записана ПФ-модель, эквивалентная ОЛ-модели, полученной в табл. 2.

Заметим, что, как и для ОЛ-модели, для ПФ-модели возможны различные реализации, структуры которых зависят от многих обстоятельств. В частности, существенными являются психофизиологические свойства и состояния специалиста. Множества таких состояний, вообще говоря, счетны, но перечислить соответствующие им реализации затруднительно. Так, например, если учитывать в рассматриваемом случае только два состояния памяти относительно заданных, и текущих значений x и y, то возможны 16 исходов с различными графами, которые должны войти в аддитивную ПФ-модель. В этой связи важной теоретической и практической задачей является установление меры деталировки реализаций в зависимости от числа психофизиологических переменных, которые на этапе проектирования информационной модели необходимо и достаточно учитывать, хотя бы для получения подходящих оценок частоты вершин и дуг результирующего ПФ-графа. Формулируя эту задачу, мы в настоящее время далеки от ее общего решения. Одним из гипотетических частных решений может быть следующее.

Ограничим число реализаций ПФ модели тремя достаточно очевидными исходами B₁, B₂ и B₃, где B₁ соответствует деятельности обученного специалиста, всегда выполняющего поблочный контроль правильности выполнения команды. Этот исход был априорно "заложен" в алгоритме (5) и реализуется в ПФ-графе "b₁" (табл. 3). Исход B₂ соответствует деятельности обученного специалиста, "самонадеянно" использующего свой профессиональный опыт и не выполняющего по этой причине инструкцию о поблочном контроле; поэтому здесь мнемоника не используется (реализация "b₂", табл. 3). Исход B₃ соответствует деятельности малообученного или "робкого" специалиста, контролирующего по мнемонике каждое свое сенсорное и моторное действие (табл. 3, реализация "b₃").

Используя модель (2), определим оценки весовых коэффициентов t_i (i=1, 2, 3), исходя из следующих правдоподобных допущений. Пусть профессиональная деятельность осуществляется в течение 25 лет, из которых 5 лет специалист обучается. Пусть, далее, в одной четверти случаев обученный специалист по тем или иным причинам не использует мнемонику. Тогда получим:

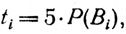
где P(B₃)=0,2; P(B₁+B₂)=0,8; P(B₂)=0,25XP(B₁+B₂)=0,2; P(B₁)=0,6, т. е. t₁=3, t₂=t₃=1. Реализации ПФ-модели алгоритма (5), взвешенные этими коэффициентами, представлены в соответствующих столбцах табл. 3, а в последнем столбце приведена сумма этих реализаций. По ней легко восстановить матрицу смежности вершин ПФ-орграфа, используемого при проектировании и исследовании информационных моделей.

Указатель литературы

1. Надежность комплексных систем "человек-техника". Вып. 2. Л., 1969, с. 16-20.

2. Зараковский Г. М. Психофизиологический анализ трудовой деятельности. М. 1965. 114 с.

3. Никифоров Г. С. Самоконтроль оператора при приеме информации от измерительного прибора. - В кн.: Экспериментальная и прикладная психология. Вып. 2. Л., Изд-во Ленингр. ун-та, 1970, с. 38-43.

4. Суходольский Г. В. О характеристиках человека при слежении. Автореф. канд. дис. Л., Изд-во Ленингр. ун-та, 1968. 12 с.