11. Выравнивание рядов

При сопоставлении двух переменных величин часто предполагают, что одна из них является аргументом (изменяется независимо), другая - функцией (меняется в зависимости от аргумента). Например, уменьшение времени выполнения какого-либо задания при выработке навыка может рассматриваться как функция от числа проб (упражнений). В таком случае варьирующие значения функции целесообразно представить в виде некоторого аналитического выражения (уравнения регрессии), т. е. выравнять статистические вариации функции, дав им в соответствии значение аргумента.

Чаще всего между аргументом х и функцией у предполагается линейная связь, т. е. у=ах+в, где а и в есть соответствующие коэффициенты. Выравнивающая линия, отвечающая такому уравнению, строится обычно по методу наименьших квадратов. Это означает, что сумма квадратов расстояний всех исходных (выравниваемых) точек до линии у=ах+в является наименьшей.

Для случая равноотстоящих значений x_i величины коэффициентов а и в в уравнении регрессии вычисляются по следующим формулам:

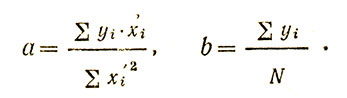
При этом исходному x_i дается численное значение x'_i по новой условной шкале с началом отсчета в середине ряда x_i, и необходимые арифметические выкладки (связанные с построением системы нормальных уравнений) значительно упрощаются.

Пример № 8. В эксперименте по выработке двигательного навыка (работа № 14 в гл. II) средние арифметические значения времени для 30 испытуемых составили по отдельным пробам (гл. II, рис. 12, кривая 2):

Вычисление параметров выравнивающей прямой ведется в особой таблице.

Таблица 16

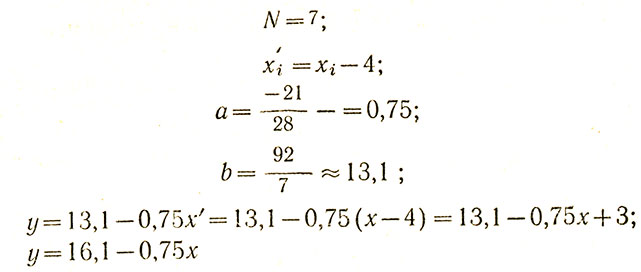
Так что в результате получено уравнение, по которому можно вычислить некоторое выравненное (линейно) значение времени (tji) для каждого номера пробы от 1 до 7 включительно. Величина а (коэффициент регрессии) выступает показателем "крутости" изменений функции (угол наклона выравнивающей прямой к оси абсцисс).

При выравнивании рядов может предполагаться и квадратичная зависимость между x и y, и вообще любая степенная. В этом случае выравнивание сводится к построению полинома некоторой n-й степени. Однако проведению таких вычислений следует предварять некоторый качественный анализ, т. е. предполагаемое объяснение степенной связи признаков и возможностей ее практического использования.

Наконец, выравнивание как устранение случайных вариаций признака (а не как получение уравнения регрессии) может быть проведено способом скользящей средней. При этом выравниваемая кривая разбивается на отдельные отрезки, в которых осуществляется линейное выравнивание. Причем эти отрезки перекрывают друг друга.

Пример № 8. Применяем способ скользящей средней, взяв за отрезок три каждых смежных значения y_i и так что

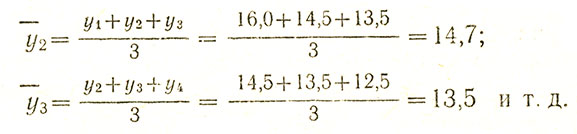
Крайние средние значения y₁ и y₇ находятся при выравнивании этим способом по пути линейной экстраполяции, т. е. путем вычисления двух линий регрессии: для x_i=1, 2, 3 и x_i=5, 6, 7 по исходным величинам y_i. Последнее осуществляется так, как показано выше, в табл. 16.