10. Корреляция и коэффициенты корреляции. Линии регрессии

В практике экспериментальных исследований нередки случаи, когда предполагается наличие связанных изменений каких-либо двух статистических признаков. Например, представляются взаимозависимыми вариации величины роста и веса тела людей (прямая связь), силы мышц и их подвижности (обратная связь) и т. д. Как указывалось в разд. 1, такого рода связи и закономерности не являются строго однозначными или функциональными; они, так же как и сами вариации признаков, являются статистическими, или корреляционными. Корреляция - это связь между статистическими вариациями (выборками) по различным признакам, между влияниями каких-либо двух факторов, формирующих данное статистическое распределение.

Коэффициент корреляции - это математический показатель силы (тесноты) связи между двумя сопоставляемыми статистическими признаками.

По какой бы формуле ни вычислялся коэффициент корреляции, его величина колеблется в пределах от -1 до +1. Смысл крайних значений коэффициента состоит в следующем:

- если коэффициент корреляции равен 1, значит, связь между признаками однозначна (функциональная, нестатистическая), по типу прямопропорциональной зависимости;

- если коэффициент равен -1, то связь также является функциональной, но по типу обратной пропорциональности;

- нулевая величина коэффициента корреляции говорит о полном отсутствии связи (по типу линейной) между сопоставляемыми признаками.

Всякое вычисленное (эмпирическое) значение коэффициента корреляции должно быть проверено на статистическую значимость (таблицы III или IV приложения).

Если эмпирическое значение меньше или равно табличному для 5-процентного уровня, корреляция не является значимой. Если вычисленное значение коэффициента корреляции больше табличного для P=0,01, корреляция статистически значима (существенна, реальна), В случае, когда величина коэффициента заключена между, двумя табличными, на практике говорят о значимости корреляции для P=0,05. Однако строго вероятностная трактовка этого факта несколько иная: мы не можем утверждать отсутствия корреляции, но ее статистически доказанного наличия также еще нет (см. разд. 7).

10-1. Простейшей формой коэффициента корреляции является коэффициент ранговой корреляции г (коэффициент Спирмена), который измеряет связь между рангами (местами) данной варианты по разным признакам, но не между собственными величинами варианты. Здесь исследуется связь скорее качественная, чем строго количественная, хотя ранг сам по себе - это уже и количественный признак.

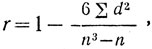
где n - объем совокупности, длина одного статистического ряда;

d - разность между рангами каждой варианты по двум коррелируемым признакам.

Пример № 5. Десять испытуемых (А, Б, В и т. д.) расположились в порядке увеличения возраста и пространственного порога (работа № 1, гл. II) в следующих последовательностях:

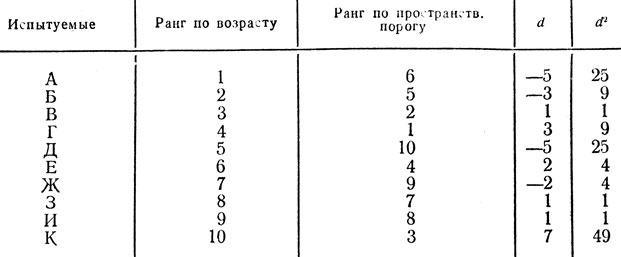
Таблица 13

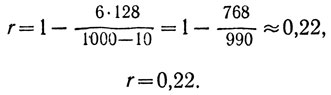
Так как по данным табл. III (приложение к гл. III) r_0,05=0,64, и эмпирическое значение r<r_0,05, корреляция между местами испытуемых по величине порогов и по возрасту не является статистически значимой.

10-2. Другой очень распространенной формой коэффициент та линейной корреляции является следующая:

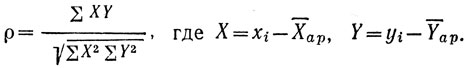
Эта формула сопоставляет сами величины признаков и в конечном счете основана на вычислении "совместной дисперсии" σ²xy двух переменных x_i и y_i и на делении ее на произведение отдельных среднеквадратических отклонений, т. е.

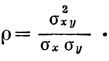
Пример вычисления. Десять испытуемых (А, Б, В и т. д.) в эксперименте по заучиванию двузначных чисел (работа № 10 в гл. II) дали по первой пробе такие результаты: 3, 4, 4, 5, 3, 4, 5, 2, 3, 5 (пример М 6). Эти же испытуемые при непроизвольном запоминании слов (работа № 8 в гл. II) имели такие показатели: 5, 9, 8, 6, 4, 5, 8, 7, 5, б (пример № 7).

Посмотрим, коррелируют ли между собой два этих показателя эффективности запоминания.

Вычисления удобнее вести в специальной таблице.

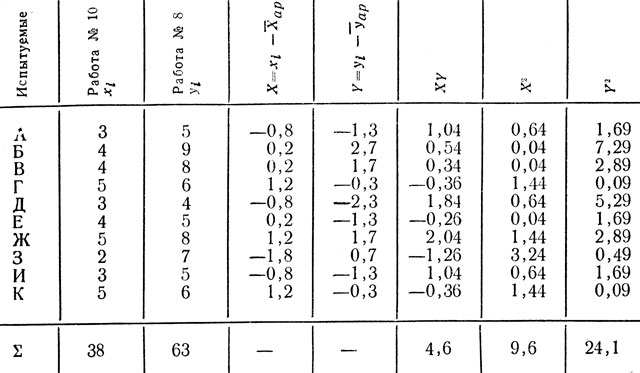
Таблица 14

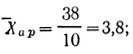
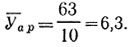
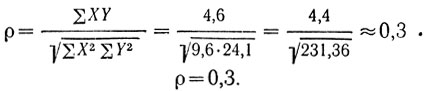
По данным табл. IV приложения, p_0,05(10)=0,632, поэтому корреляция между двумя показателями эффективности памяти данной группы испытуемых не является статистически значимой.

Выявлению корреляционной зависимости способствуют и определенные табличные и графические методы. Последние могут оказаться полезными не только сами по себе, но и как приемы, предваряющие непосредственное вычисление коэффициента корреляции, как выявление общего направления рассматриваемой связи двух признаков.

10-3. Групповая таблица (или корреляционная решетка) - результат совместной группировки двух варьирующих рядов, которые исследуются на корреляцию. В клетках таблицы проставляется число вариант с данными параметрами.

Для примеров № 6 и 7 (по данным предшествующей табл. 14) групповая таблица имеет следующий вид:

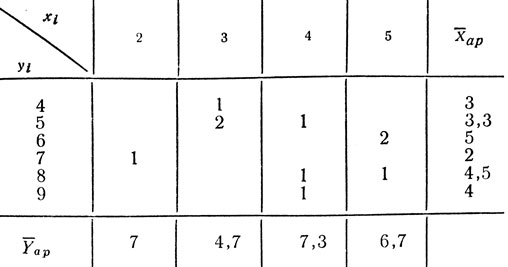
Таблица 15

Как видно из табл. 15, рассматриваемые показатели не обнаруживают какой-либо системы в расположении; стало быть, мы не вправе предполагать корреляции между ними.

Полезным дополнением корреляционной решетки является вычисление средних арифметических значений одного из варьирующих признаков при неизменности другого (и наоборот).

В табл. 15 такие средние значения представлены в нижней строке и в крайнем правом столбце. Столбец величин X_ap представляет собой средние арифметические значения признака хи соответствующие каждому значению y_i: 4, 5, 6 и т. д. Строка величин Y_ap в табл. 15 - это средние величины признака y_i в их соответствии значениям x_i.

Корреляционное поле - совокупность точек на плоскости, у которой оси абсцисс и ординат есть значения двух сопоставляемых статистических признаков.

Скажем, для предшествующих примеров № 6 и 7 по данным табл. 15 на рис. 22 построено корреляционное поле, где по оси абсцисс отложены величины x₁ - объем запоминания после первого предъявления, а по оси ординат - объем непроизвольного запоминания слов - величины y_i. Причем точки с координатами 3,5 и 5,6, обведенные на рис. 22 кружками, встречаются в корреляционной решетке по два раза каждая (см. табл. 15).

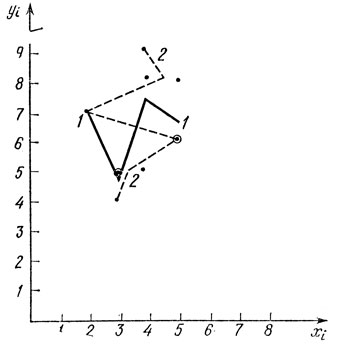
Рис. 22. Корреляционное поле для примеров № 5 и № 6. 1 - линия регрессии y_i в зависимости от условного аргумента x_i, 2 - линия регрессии xi в зависимости от условного аргумента y_i

Линия 1 на рис. 22 построена по данным строки y_ap табл. 15, линия 2 - по данным столбца X_ap этой же таблицы. Эти линии называют линиями регрессии - линиями, отображающими зависимости каждого статистического признака от средней величины другого статистического признака.

Сама по себе форма расположения точек на корреляционном поле и контур соответствующих линий регрессии выступают наглядными показателями тесноты связи, существующей между двумя сопоставляемыми признаками.

Ведь если бы увеличение x_i всегда влекло за собой увеличение y_i, то точки поля располагались бы по линии 1 на рис. 23, для которой коэффициент корреляции p=1.

Линия 2 на рис. 23 соответствует обратно пропорциональной связи между признаками x_i и y_i когда величина p=-1.

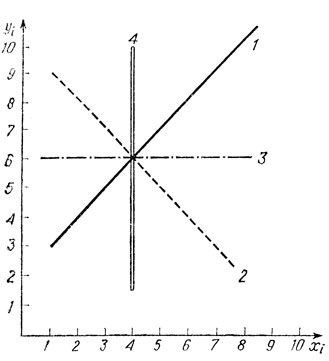
Рис. 23. Линии регрессии в случаях крайних значений коэффициента линейной корреляции двух признаков (x и y): 1 - коэффициент корреляции p=1, 2 - коэффициент корреляции p=-1, 3, 4 - коэффициент корреляции p=0

Факт отсутствия корреляции (p=0) соответствует на корреляционном поле линиям 3 и 4 (рис. 23). Мы видим, что линии регрессии 1 и 2 на рис. 22 стремятся именно к контурам линий 3 и 4 на рис. 23, и уже одно это свидетельствует об отсутствии "тесной" связи (до вычисления коэффициента p).