Г. В. Суходолъский. Анализ и синтез равновесных структур (основы теории и психологические приложения)

1. Структура. Граф как математическая модель структуры

1. Понятие структуры. Термин "структура" и производная от него дефиниция "структурный" сегодня в психологической науке применяются очень широко. Говорят и пишут о "структуре сознания", "структуре перцептивных процессов", "структуре личности", о "структурных характеристиках" образов, памяти, интеллекта. Пожалуй, не будет ошибкой предположить, что нет такого психического явления, к которому не применялись бы кем-нибудь эти термины. Однако в понимании того, что собой представляет структура, нет единогласия. Здесь можно выделить следующие трактовки.

1) Структура - это либо "элементный" состав, строение явления, либо взаимосвязи в нем. При таких трактовках "структурные характеристики" сводятся либо к рассмотрению "элементного" состава, либо к анализу существенных связей, внутренних закономерностей явления.

2) Структура - это множество взаимосвязей между элементами или множество элементов, взаимосвязанных между собой. Здесь уже фигурируют совместно и "элементный" состав, и взаимосвязи. Причем акцент делается то на элементах, то на связях и распространяется на понимание "структурных характеристик".

3) Структура - это система взаимосвязанных элементов. Здесь понятие структуры по объему приближается к понятию системы, и соответствующие термины - почти синонимы. Во избежание синонимии К. К. Платонов предлагает закрепить за понятием структуры онтологический, "объективный" смысл, а за понятием системы - гносеологический, "субъективный" смысл: система есть субъективное отображение объективной структуры [6, с. 27].

Итак, имеется пять трактовок понятия структуры. Две первые - только элементы или только связи,- с нашей точки зрения, неверны. Две последующие представляются верными, но узкими (множество взаимосвязей элементов или множество взаимосвязанных элементов). Наконец, последняя, пятая - верная, но широкая, так как определяет структуру как систему.

Теперь о "структурных характеристиках" или, лучше сказать, о характеристиках структуры.

В психологической литературе, насколько можно судить, часто используются следующие характеристики структур: 1) иерархичность, т. е. наличие соподчиненных уровней структуры; 2) связность, т. е. количественная характеристика целостности (или, наоборот, автономности); 3) сложность, т. е. количество элементов и связей; 4) динамичность как изменчивость во времени (альтернатива - статичность); 5) пространственно-временная (и прочая) интерпретация элементов, связей и структуры в целом, т. е. ее верифицированность. Реже используются такие характеристики структуры, как: б) гетерогенность (гомогенность) элементов и связей; 7) адекватность как соответствие концептуальной модели объективной структуре явления; 8) детальность, дифференцированность рассмотрения (свернутость или развернутость представления). И, наконец, почти не используются такие характеристики структур, как: 9) мерность - необходимая и достаточная полнота теоретического описания; 10) открытость (замкнутость) как свойство взаимодействовать с другими структурами; 11) стохастичность как однозначность или неоднозначность в проявлениях при стационарных условиях; 12) равновесность (неравповесность).

Уже из перечисления характеристик структуры видно, что для их отображения в психологической теории и практике необходим соответствующий понятийный аппарат, желательно - математический. Какие же из известных сегодня математических средств наилучшим образом пригодны для описания структур и структурных характеристик психических явлений? Это графы.

2. Граф как математическая модель структуры. Сегодня графы "завоевывают" научный мир. И это касается не только технических, экономических, социальных наук. Широкое распространение графы получили и в психологии: для описания и анализа потоков информации в системах контроля и управления; для описания и анализа организационной структуры трудового коллектива - формальной и неформальной; для описания и анализа того, как человеческий мозг отображает внешний мир и себя самого и преобразует их своими действиями; для описания памяти специалиста, принимающего решение о последовательности действий, необходимых для управления процессом; для изображения логических особенностей знания и научения, умения решать задачи; для изображения и оценки массовых коммуникаций.

Наиболее употребительными являются графический и матричный способы задания графов. Например, для графа, показанного на рис. 1, одна из матриц - матрица смежности выглядит так:

В этой матрице строки и столбы нумеруются как и вершины графа; элементы a_ij характеризуют имеющиеся дуги (если дуги нет, то а_ij - 0).

Легко видеть, что граф - это математическая структура. По своей сути графы являются идеальными математическими моделями различных явлений. Поэтому способы задания, исследования, построения графов, изучения их свойств выступают в качестве способов математического изучения структур, в частности, психических.

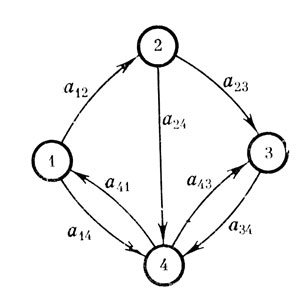
Рис. 1. Ориентированный граф (орграф). 'Кружками' обозначены его вер. тины, они произвольно пронумерованы. 'Стрелками' обозначены дуги, количественно характеризуемые мерами а_ij, где i - номер вершины, из которой дуга исходит, j - номер вершины, в которую дуга входит

В существующей теории графов разнообразие видов графов, их свойств и специфики изучено далеко не равномерно. Пожалуй, наимение изучены как раз те виды графов, особенности которых наиболее полно соответствуют перечисленным выше характеристикам структур. Это прежде всего касается иерархичности, динамичности, стохастичности, открытости и равновесности. Дальнейшее изложение будет посвящено анализу и синтезу специальных графов как математических моделей психических структур, которым свойственны указанные характеристики. Учитывая, что граф и его матрица смежности суть эквивалентные математические модели структур, термины "граф", "матрица", "структура" далее употребляются как синонимы.