2. Равновесные структуры

1. Определение равновесной структуры. Равновесной будем называть структуру, каждый элемент которой находится в равновесии (статическом или динамическом) с другими элементами и внешней средой.

Символически можно пояснить равновесность для элемента, как это сделано на рис. 2А, если

∑_ВХ=∑_ВЫХ (1)

Научная интерпретация равновесности может быть дана, например, с позиций законов сохранения.

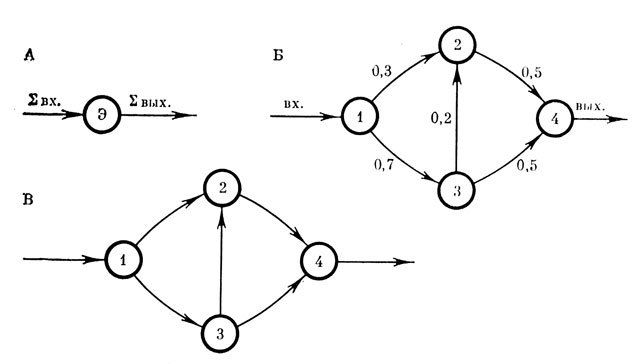
Рис. 2. Равновесные и неравновесные структуры. А. 'Равновесный' элемент структуры (сумма 'вх' равна сумме 'вых'). Б. Равновесный орграф (единицы на 'вх' и 'вых' опущены). В. Неравновесный граф Бержа

По определению, равновесным назовем граф, для каждой вершины которого выполняется равенство (1). Для матрицы смежности это означает, что суммы элементов в одноименных строках и столбцах равны. Например, для равновесного графа на рис. 2Б матрица имеет вид:

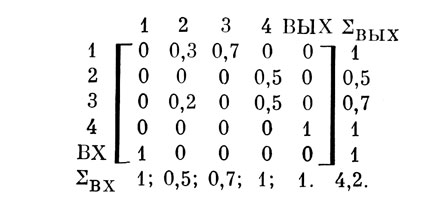
Типичным равновесным графом, широко используемым в психологии, является корреляционный граф [101. Соответственно, корреляционная матрица - равновесная.

Отрицанием равновесной структуры является неравновесная структура. Неравновесной будем называть структуру, у которой равновесность отсутствует, хотя бы для одного из элементов. Например, граф Бержа на рис. 2В неравновесный. Легко убедиться, что для неравновесного графа (см. рис. 2В) суммы в одноименных строках и столбцах матрицы смежности не равны.

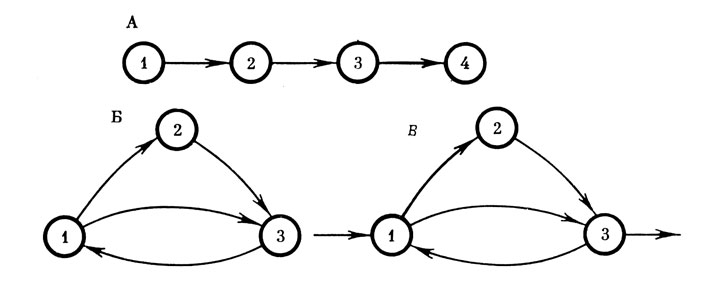
Рис. 3. Различение входов и выходов графа. А. 'вх' и 'вых' не помечены, но различаются. Б. 'вх' и 'вых' без пометки не различаются. В. 'вх' и 'вых' графа помечены 'стрелками' и отличаются от прочих вершин

Здесь необходимо сделать важное пояснение. Общепринятым является такое изображение графов, при котором "начальную" и "конечную" вершины (так называемые "исток" и "сток" или "вход" и "выход" графа) ничто не выделяет специально. В некоторых случаях этого и не требуется (рис. 3А). Но чаще всего создается неопределенность (рис. 3Б). Нами используется пометка "вх" и "вых" графов (рис. 2, рис. 3В), благодаря чему равновесные и неравновесные графы однозначно различаются. Кроме того наличие дуги "вх" и дуги "вых" как бы "включает" граф во внешнюю среду, рассматриваемую как дополнительная вершина.

Возникает вопрос, какие преимущества имеют равновесные структуры. Сейчас очевидным является одно, но существенное преимущество: имманентным свойством равновесной структуры является последовательность состояний (или действий), не имеющая разрывов. Примем как аксиому следующее предложение: любой путь (Путь в графе - это последовательность смежных вершин и дуг [3]) между вершинами в графе, если он существует, непрерывен (см. рис. 4).

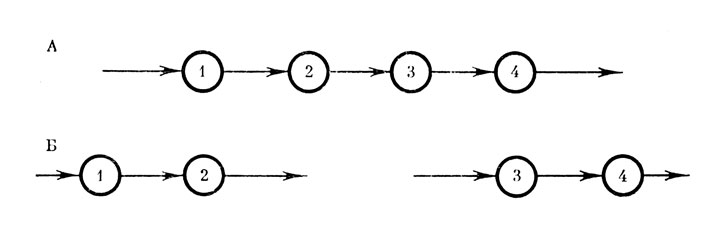
Рис. 4. Непрерывность и пути в графе. А. Граф состоит из одного пути, очевидно, непрерывного. Б. Граф имеет две связных компоненты, не соединенных путем

В связи с равновесностью и неравновесностью структур возникает и другой вопрос. Как восстановить "нарушенную" равновесность? Можно показать, что решение этого вопроса сводится к двум другим: 1) как разложить неравновесную структуру на равновесную и неравновесный "остаток", минимальный в некотором смысле? 2) Как дополнить неравновесную структуру до "ближайшей" равновесной? Или, что то же самое, - как разложить равновесную структуру на две неравновесных подструктуры, одна из которых минимальна в заданном смысле? Можем сказать, что, в первом приближении, ответы на эти вопросы получены.

2. Иерархия равновесных структур. Введем понятия под- и надструктуры. В любой структуре, имеющей более одного элемента, можно выделить части. Их и назовем подструктурами. Подструктуры, очевидно, сами являются структурами (хотя бы из одного элемента). Договоримся считать, что для выделения подструктур из некоторой структуры до л латы быть соответствующие операции, применение которых составляет процедуру анализа. С другой стороны, относительно своих подструктур всякая структура выступает как над- (или мета-) структура. Метаструктура должна синтезироваться из структур. Для этого, очевидно, нужны операции синтеза.

Введем свою интерпретацию понятий уровня, ранга структуры и иерархической структуры. Уровнем структуры будем называть некоторую подструктуру, имеющую самостоятельный смысл. Уровни как-либо обозначаются и нумеруются (от нуля). Заметим, что "внутри" уровня тоже можно выделять подструктуры. Иерархической назовем структуру, имеющую более одного уровпя. При одном уровне структура неиерархическая. Ранг структуры определим как число уровней без одного. Следовательно, неиерархическая структура имеет "нулевой" ранг.

Рассмотрим некоторые важные виды равновесных мета-структур, с точки зрения их формы (рис. 5). Цепь - открытая метаструктура, вершины и линии которой суть подструктуры, записанные в свернутой форме (свертка подструктуры в вершину или линию - специальные операции). Лепесток - полуоткрытая метаструктура из двух подструктур. Ее петля - это свертка в линию одной подструктуры, а вершина - свертка (в вершину) другой. Цветок - полуоткрытая метаструктура из произвольного числа подструктур.

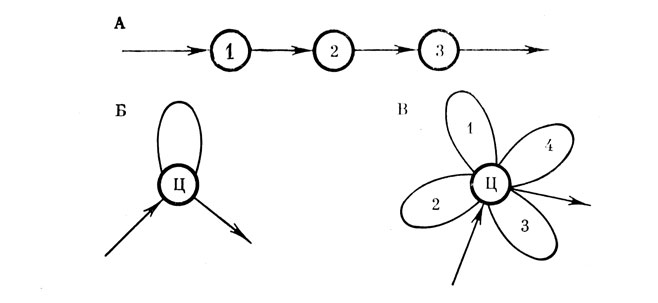
Рис. 5. Некоторые формы равновесных метаструктур. А. Цепь.Б. Лепесток. В. Цветок, его лепестки произвольно перенумерованы; 'Ц' - центр цветка

Введем понятие случайной структуры. Случайной структурой (ССТ) назовем структуру, которая в результате опыта принимает вид одной из множества возможных структур, априори неизвестно какой. Апостериори любая структура является неслучайной. Неслучайную структуру, появившуюся в результате опыта, назовем реализацией ССТ. Легко видеть, что реализация есть подструктура ССТ, характеризуемая вероятностью. Очевидно, полной количественной характеристикой ССТ является распределение вероятностей ее реализаций. Неполные количественные характеристики ССТ в виде ее математического ожидания и дисперсии определим ниже.

Введем понятие равновесной случайной структуры. Равновесной назовем ССТ, все реализации которой равновесны. Типичный пример равновесной ССТ - это корреляционная матрица генеральной совокупности. Ее реализациями являются выборочные корреляционные (под)матрицы. Отрицанием равновесной ССТ является неравновесная ССТ. Неравновесной назовем ССТ, для которой хотя бы одна реализация неравновесна. Типичный пример неравновесной ССТ - алгоритмы решения задач, записанные по А. А. Ляпунову и Г. А. Шестопалу [5].

Перейдем теперь к вопросам анализа и синтеза равновесных структур. Так как операции анализа, которые будут предложены, в известном смысле обратны к операциям синтеза, начнем с синтеза.