3. Синтез равновесных структур

Как известно, анализ - это расчленение целого на части, а синтез - восстановление целого из частей. Анализ и синтез лишь относительно самостоятельны. Согласно С. Л. Рубинштейну, "...анализ и синтез... непрерывно переходят друг в друга. Анализ без синтеза порочен..." [7, с. 296]. Несмотря на эти фундаментальные положения психологической науки, в настоящее время у нас в психологии преимущественно ограничиваются анализом психических явлений. Причина, видимо, в том, что недостаточно разработан категориальный и операциональный аппарат синтеза.

1. Категории синтеза в психологии. Если понимать синтез как восстановление целого из частей, то на вербальном уровне обычно используются лишь три категории синтеза: "систематизация", "обобщение" и "ассоциирование" ("замыкание"). Семантика первой ясна - систематизация есть синтез системы через упорядочение частей. А вот категория "обобщения" двусмысленна. Остановимся на ней подробнее.

Наиболее распространено понимание обобщения как абстракции того общего, что имеется в единичном, частном, особенном. На это указывал и С. Л. Рубинштейн. Нам представляется очевидным, что в таком понимании содержится явное противоречие с понятием синтеза. Абстракция есть отвлечение и извлечение части из целого, она есть элемент анализа, но не синтеза.

Вторая трактовка категории "обобщение" тоже дана С. Л. Рубинштейном. "Когда мысль возвращается к единичному, от которого она оттолкнулась на своем пути к общему, она возвращается к нему обогащенной, единичное и особенное выступает... уже в новом аспекте... в единстве и различии единичного, особенного и общего" [7, с. 299]. Таким образом, обобщение как результат мыслительной деятельности есть единство и различие единичного, особенного и общего. Какой же математический аппарат в состоянии отобразить это единство и различие единичного, особенного и общего? Иначе говоря, какие из математических операций над структурами могут быть моделями операции обобщения?

2. Математические модели обобщения. Объединение - вот наиболее распространенная операция синтеза некоторой логической структуры из частей. Но объединение, приводя к единству единичного, особенного и общего, совершенно затушевывает, снимает различия между ними. Ниже это будет показано весьма наглядно. Таким образом, объединение полностью не моделирует обобщение, хотя и является операцией синтеза.

Обобщение - это новая математическая операция, смысл которой раскроем в следующих определениях.

Определение 1. Даны: матрица А с размерами nхm и матрица В с размерами рxq, причем в общем случае n≠р и m≠q. Базовой матрицей (матрицей-основой [12, с. 61]) назовем матрицу С⁽⁰⁾, номера строк и столбцов которой получены объединением номеров строк и столбцов в матрицах А и В, а все элементы - нули.

Например, даны матрицы:

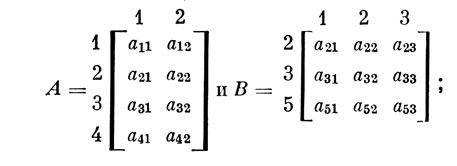
тогда базовой для них будет матрица:

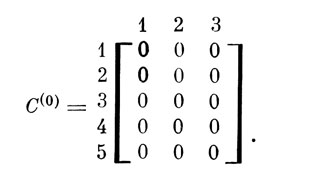
Определение 2. Назовем матрицу A⁽⁰⁾ матрицей в базовой форме, если к А приписаны строки или столбцы, или те и другие из нулевых элементов, дополняющие А до А⁽⁰⁾. Например, приводя к базовой форме матрицы А и В, получим:

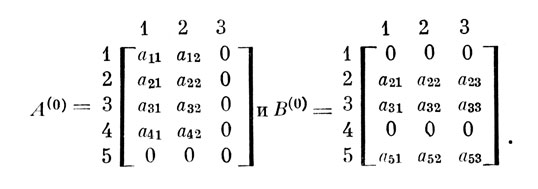
Определение 3. Назовем матрицу С обобщением матриц A и B, если

A⁽⁰⁾+B⁽⁰⁾=C

где "+" обозначает обычное суммирование матриц.

Определение 4. Назовем обобщением операцию получения матрицы С из матриц А и В разной формы:

C=AOB=A⁽⁰⁾+B⁽⁰⁾

и вообще:

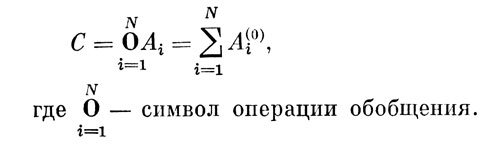
В частности, для матриц А и B, рассмотренных выше, матрица-обобщение выглядит так:

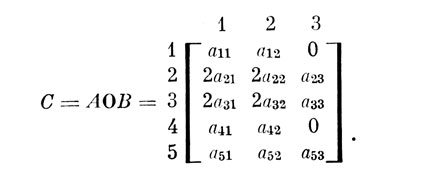
Теперь для сравнения рассмотрим, как выглядит объединение и пересечение матриц А, В:

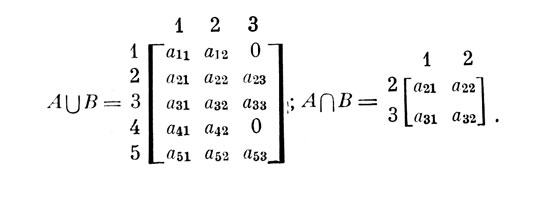
Можно видеть, что обобщение двух "булевых" матриц (при a_ij=1 или 0) интерпретируется как обычная (не булева) сумма объединения и пересечения (в базисной форме). Но в общем случае (например, если a_ij - действительные числа) обобщение незачем сводить (хотя и можно) к суммированию "булевых" матриц.

Теперь пора сформулировать более общую идею. Обобщение в широком смысле можно математически рассматривать как родовую операцию, основанную на алгебраическом суммировании. Тогда, в зависимости от вида алгебры, можно понять видовые операции, моделирующие те или иные формы (а может быть, аспекты, грани) обобщения как психического феномена: объединение - это суммирование по правилам алгебры двузначной логики, оно моделирует единство единичного, особенного и общего; обобщение в узком смысле, как оно введено выше, - это суммирование по правилам обычной алгебры; оно моделирует совместно и единство, и различие единичного, особенного и общего. Можно представить, что существуют разновидности обобщения в широком смысле и для любых других алгебр, моделирующие неизвестные сегодня формы (или особенности) обобщения как психического, физиологического, "нейронного" феномена.

В дальнейшем изложении будет использоваться модель обобщения в узком смысле, поэтому будем говорить кратко "обобщение". Рассмотрим его математические свойства.

3. Математические свойства операции обобщения. Сначала покажем, что обобщение как операция существенным образом расширяет возможности суммирования в матричной алгебре.

Сейчас известны два вида суммирования матриц: обычная и "прямая" суммы (рис. 6, 1 и 3). Обычная сумма в матричной алгебре разрешена лишь для конгруэнтных матриц; ее элементы определяются известным правилом: с_ij=a_ij+b_ij. "Прямая" сумма [2, с. 16] используется для непересекающихся матриц (любой формы); ее элементы определяются правилом:

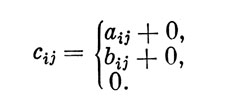
Легко видеть (рис. 6, 2), что обобщение "заполняет" интервал возможностей между этими случаями, которые теперь выступают как предельные, выводимые из обобщения путем наложения ограничений (конгруэнтность, либо отсутствие пересечений). Действительно, при обобщении элементы результирующей матрицы определяются правилом (см. рис. 6, 2), в котором объединяются оба предыдущих:

Рассмотрим теперь операцию обобщения с позиций абстрактной алгебры. С этих позиций класс числовых матриц, элементы которых суть действительные числа (или их символы), является коммутативным кольцом без единицы относительно операций обобщения и умножения по Адамару. Действительно:

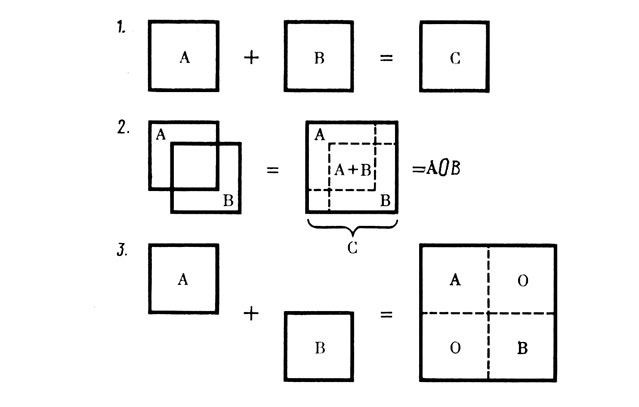
Рис. 6. Обычное (1), 'прямое' (3) суммирование матриц и обобщение (2)

1) Этот класс есть аддитивная группа (коммутативная и ассоциативная по обобщению):

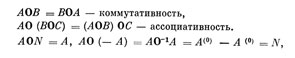
где N - базисная "нуль"-матрица, "О^-1" - символ операции, обратной к обобщению (далее, используем ее в качестве одной из операций анализа).

2) Этот класс - коммутативная и ассоциативная группа по умножению Адамара:

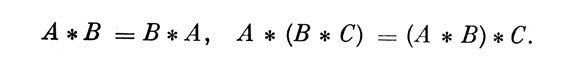
3) Для этого класса матриц выполняются дистрибутивные законы (умножения слева и справа):

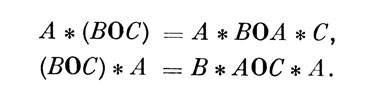
4) Указанные операции, очевидно, приводят к "действительным" матрицам, т. е. класс замкнут относительно обобщения и умножения по Адамару.

4. Обобщение равновесных структур. Теорема 1. Обобщение равновесных структур есть равновесная структура. Доказательство сводится к следующему индуктивному рассуждению.

1) Для i-той вершины любой j-той из обобщаемых равновесных структур, по определению, справедливо, что суммарная частота "вх" равна суммарной частоте "вых":

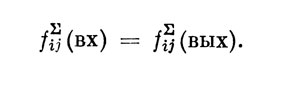
2) Для i-той вершины обобщения из n равновесных структур, очевидно, справедливо:

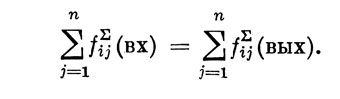
3) То же самое справедливо и для обобщения с n+1-ой равновесной структурой.

Следствие 1. Неравновесная структура не может быть обобщением равновесных структур: либо допущена ошибка при выполнении операции, либо хотя бы одна из обобщаемых структур неравновесна.

Следствие 2. Обобщение равновесной структуры самой с собой не нарушает равновесности.

Теорема 2. Равновесная структура представима в виде пути, либо обобщения путей. Для доказательства проведем следующее рассуждение. Выделим какой-нибудь путь, ведущий от "вх" к "вых" структуры. Он либо исчерпывает структуру, и тогда теорема доказана, либо не исчерпывает ее: "отслоим" подструктуру выделенного пути (она, по определению, равновесна) от исходной структуры; остаток, согласно теореме 1, есть равновесная структура. Далее, рассуждение рекуррентно повторяется.

5. Взвешивание (нормирование) равновесных структур. Из следствия 2 теоремы 1 явствует, что умножение равновесной структуры на скаляр не нарушает равновесия. Отекла следует, что обобщение взвешенных равновесных структур (А_i) дает равновесную метаструктуру (В):

где f_i - скаляры, причем, если fi>1, то имеет место взвешивание структур, а если 0≤fi≤1, то имеет место нормирование.

6. Математическое ожидание и дисперсия равновесной случайной структуры. Пусть, по определению, случайная структура А задана на множестве своих реализаций законом распределения их вероятностей. Тогда имеют смысл такие количественные характеристики этой структуры, как математическое ожидание и дисперсия.

Математическое ожидание равновесной случайной структуры А есть неслучайная равновесная структура

где А_i - подматрицы реализаций A, р_i - их вероятности: ∑^N_i=1p_i=1; М (А) - математическое ожидание, характеризующее позицию А на множестве возможных реализаций.

Дисперсия равновесной случайной структуры А есть неслучайная (в общем случае неравновесная) структура, матрица которой определяется уравнением:

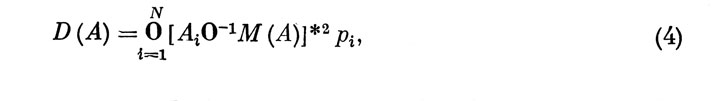
где О^-1 - операция "отслаивания", обратная к обобщению, [В]^*2 =В_*В - обозначает возведение матрицы В в квадрат на основе умножения по Адамару (Умножение по Адамару и, в частности, возведение в степень, нарушает равновесность во всех случаях, кроме тех, когда В есть симметричная матрица или матрица простого взвешенного пути. Поэтому D (А) и не является в общем случае равновесной матрицей). D (А) можно трактовать как совокупную характеристику изменчивости случайной структуры.

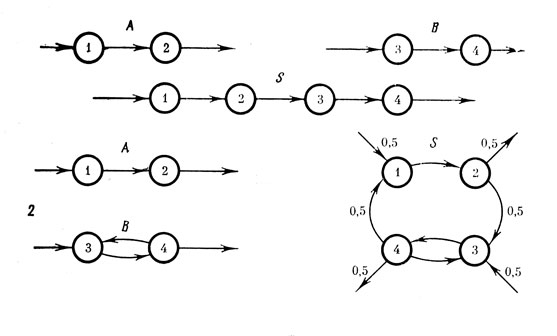
Рис. 7. Соединения структур. А и В - соединяемые структуры, S - мотаструктуры, полученные в результате: 1 - достоверного соединении; 2 - случайного соединения без повторений соединяемых структур, в предположении из независимости и равновероятности появления в метаструктуре

Необходимо заметить, что математическое ожидание и дисперсия применимы и к неравновесным ССТ; при этом формулы (3) и (4) остаются справедливыми.

Выше, говоря о категориях синтеза в психологии, мы упомянули ассоциирование. Психологический смысл ассоциаций и их физиологические основы изучены, а вот математические модели, насколько можно судить,- нет. Однако, на основе операции обобщения можно ввести математическую модель ассоциации, которую назовем соединением.

7. Соединения равновесных структур. Операциональное определение соединений задано формулой:

где A_i - соединяемые структуры, Z - матрица "переходов" от структуры к структуре, S - матрица соединения (матрица метаструктуры). Нами разработаны классификация и техника соединений, используя которые можно синтезировать теоретически - любые, а практически - достаточно сложные структуры (содержащие до нескольких сотен элементов).

Здесь невозможно изложить всю классификацию и принципы техники соединений. Поэтому ограничимся двумя простыми примерами. На рис. 7 показаны две разновидности соединений: 1 - достоверное, при котором единственная последовательность структур в метаструк-туре достоверно известна, и 2 - случайное соединение без повторений, при котором возможны две последовательности, две реализации метаструктуры, принятые равновозможными.

Соединения структуры можно строить и на основе операции объединения. Формула соединений здесь аналогична (5):

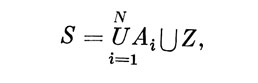
но возможен лишь один вид соединений - достоверные, и метаструктуры получаются всегда в виде графов Бержа. Необходимо отметить, что разработанный сейчас аппарат соединений с очевидностью моделирует не все известные в психологии ассоциации, а лишь "ассоциации последовательности" [8, с. 281]. Моделирование других видов ассоциаций, возможно, потребует привлечения дополнительных операций на структурах (например, декартова произведения, суперпозиции, умножения графов [3]).