4. Анализ равновесных структур

1. Два направления анализа. Целесообразно выделить две разновидности анализа: анализ психической структуры с целью ее моделирования и исследование модели структуры для выявления ее характеристик.

Анализ объективно существующей психической структуры с целью ее математического моделирования можно лаконично назвать "моделированием структуры", Если объектом анализа является случайная структура, то возможны два пути моделирования - апостериорный и априорный. Апостериорное моделирование есть статистический путь наблюдения и регистрации реализаций ССТ. Методологически и методически важнейшим условием здесь является репрезентативность выборки. Априорное моделирование - это путь теоретический. Разумеется, он предполагает наличие некоторой "опорной" апостериорной информации. Но он возможен и выгоден тогда, когда невозможен или невыгоден эмпирический путь. Там, где моделируются структуры алгоритмического типа, априорное моделирование сводится, во-первых, к построению алгоритмов на языке А. А. Ляпунова, во-вторых, к перечислению возможных реализаций по комбинациям логических условий и, в-третьих, к вероятностной экспертной оценке и обобщению этих реализаций. Там, где моделируются структуры неалгоритмического типа (например, структура личности), априорное моделирование сводится к созданию теоретических концепций, которые, далее, формализуются и становятся "рабочими" гипотезами для эмпирии.

Исследование математических моделей психических структур, может быть, с нашей точки зрения, проведено в трех направлениях. Во-первых, в направлении верификации модели (типичный пример - верификация факторных структур). Во-вторых, в направлении оценки количественных характеристик модели (сложности, связности, надежности и т. п. Типичный пример здесь - предложенные Г. М. Зараковским коэффициенты [1]). В-третьих, в направлении "машинного" моделирования "поведения" моделей (например, методами Монте-Карло).

Для всех перечисленных направлений анализа могут оказаться полезными операции, обратные к операциям синтеза.

2. Операции анализа, обратные к обобщению и соединению. Ограничимся здесь рассмотрением только двух операций: отслаивания (она упоминалась выше) и отрезания.

Отслаивание как математическая операция, обратная к обобщению (ее символ "О^-1"), предназначена для выделения подструктур из структуры. Математические свойства отслаивания определяются рассмотренными выше свойствами обобщения. Операциональный смысл отслаивания проще всего интерпретировать как "вычитание" неконгруэнтных матриц.

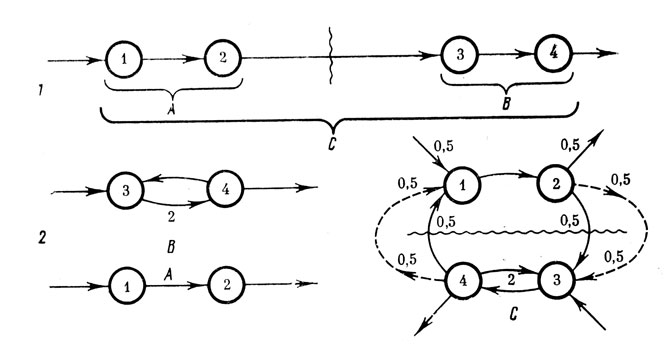
Рис. 8. Отрезание структуры от метаструктуры. С - метаструктуры, В - отрезаемые структуры, А - результаты. 1 - простейший случай (метаструктура является цепью); 2 - более сложный случай (метаструктура - сложная сеть). Волнистой чертой показаны места разреза связей

Психологический смысл этой операции - конкретизация как выделение частного, единичного, отдельного из обобщенного. Здесь существенный интерес представляет следующее. Широко распространено мнение, что обобщение "дает" экономию памяти (в частности, в связи с символическим перекодированием и укрупнением оперативных единиц информации). Математические модели обобщения и конкретизации позволяют считать это мнение верным лишь отчасти. А именно: экономия памяти имеет место лишь вместе с потерей информации о конкретном. Для того чтобы информация не терялась, необходима дополнительная память на все (и каждую) подструктуры - единичные, особенные и общие. Только тогда через обобщение можно реконструировать конкретное. Иначе говоря, если

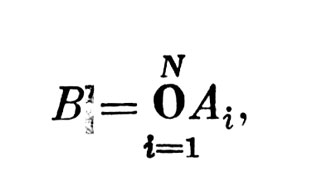
то необходимо помнить не только В, но и все А_i.

Отрезание как математическая операция обратна к соединению и тоже предназначена для выделения подструктур из структуры. Математический смысл отрезания демонстрирует" рис. 8. В простейшем случае цепи (С) структура В отрезается от нее, и остается искомая структура А. В более сложном (но не самом сложном) случае (рис. 8, 2) разрезаемые дуги с их частотами "приплюсовываются к "вх" и "вых" соответствующих вершин. Таким образом, если дана структура С и известна подструктура В, то искомая подструктура А определяется матричным уравнением:

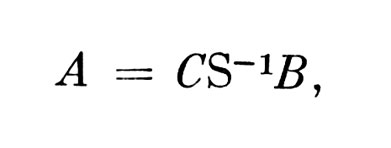
где "S^-1" - символ операции отрезания подструктуры, записанной после него, от подструктуры, записанной перед ним.

Так как соединение основано на обобщении (5), то психологический смысл отрезания может состоять, во-первых, в "диссоциации", и, во-вторых, - тоже в конкретизации, хотя последнее менее очевидно.