1. Задача теории

Если теория решений уделяет главное внимание особенностям принятия решения при изменении мотивации, но при постоянных по величине физических параметрах стимулов, то перед теорией, изучающей сенсорные процессы в обнаружении, стоит обратная задача: определение связи между мерой обнаружения и физическими параметрами стимулов при единообразных условиях принятия решения.

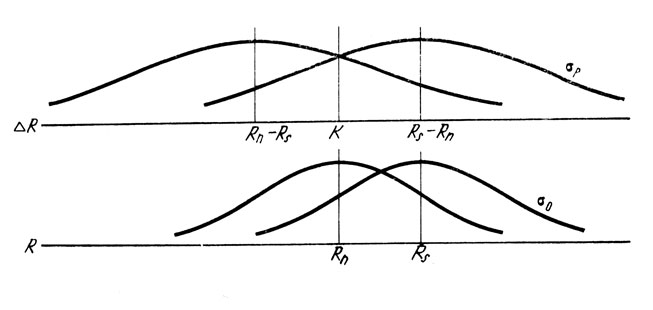
Рис. 1

Для целей сенсорной теории в обнаружении обычно используется метод "вынужденного выбора": наблюдателю предъявляются пары стимулов, один из которых включает в себя сигнал. Предполагается давать ответ, в каком из предъявлений, первом или втором, подмешан сигнал (Варианты этого метода допускают предъявление наблюдателю серии из т стимулов (m=3, 4, ...), лишь один из которых содержит сигнал. Поскольку, однако,'"основные экспериментальные материалы были получены с использованием двух стимулов, то в дальнейшем, в целях упрощения изложения, мы будем рассматривать лишь этот вариант).

Рассмотрим графическую иллюстрацию этого метода (рис. 1).

Пусть R - ось сенсорных эффектов. Общепризнанно, что повторные предъявления относительно коротких сти-мульных интервалов (шума или сигнал + шума) вызывают у наблюдателя не один и тот же сенсорный эффект, а их распределение. Тогда положим, что кривая со средним R_n - плотность вероятности того, что стимул n (шум) производит эффект R, а кривая со средним R_s - плотность вероятности того, что s (сигнал + шум) производит эффект R.

В каждой пробе наблюдатель сравнивает два ощущения, вызванные предъявлением шума и смеси сигнала с шумом. Результат этого сравнения описывается распределениями ощущений различия на оси ΔR, имеющими средние, равные разности средних первых двух распределений (R_s-R_n, R_n-R_s) и дисперсию, равную для нормальных распределений сумме дисперсий (σ²_р - 2σ²₀); одна из кривых на оси ΔR (правая) - для пар с порядком следования ns, другая - для sn. Поскольку априорная вероятность появления сигнала неизменно равна 0,5 и возможен лишь один правильный ответ, постольку положение границы К, определяющей правило принятия решения, при этом экспериментальном методе фиксировано и совпадает с нулем оси ΔR. Таким образом, если ощущение различия, вызванное предъявлением пары стимулов, положительно, то принимается решение, что сигнал был во втором стимуле пары, если отрицательно, то - в первом (в зависимости от действительного порядка стимулов в паре, ответ может оказаться как правильным, так и неправильным).

Если допустить, что распределения нормальны, то можно установить однозначную связь между мерой обнаружения, выраженной относительным числом правильных ответов, и параметрами распределений. Действительно, если σ_р - стандартное отклонение распределения сенсорных различий, то нормированное по стандартному отклонению расстояние между средними на оси ΔR (d') выразится как

Тогда относительное число правильных ответов (p), равное плошади под правой кривой распределения в области положительных значений AR (илиг что то же самое, площади под левой кривой в области отрицательных значений), связывается с величиной d' соотношением:

где F - знак интеграла Лапласа.

Таким образом, основная задача теории, изучающей сенсорные процессы в обнаружении,- выразить d' через физические параметры стимулов.

Рассмотрим, как подходят к решению этой задачи теория идеальных наблюдателей и энергетическая статистическая теория.