II. Влияние материала

§ 1. Влияние расположения элементов в ряду

Организация материала в ряды из последовательных элементов вызывает два общих эффекта: а) образование между несмежными элементами ряда "дистантных" ассоциаций, которые в зависимости от их направления называются антероградными или ретроградными ассоциациями; б) эффекты торможения, которые влияют на сохранение элементов в зависимости от их относительного положения внутри ряда.

А. "Дистантные" ассоциации

Если испытуемый должен заучить ряд элементов, соблюдая их порядок, то между последовательными элементами образуются такие ассоциации, что каждый элемент становится стимулом по отношению к последующему элементу и ответом по отношению к предшествующему (за исключением первого и последнего стимулов ряда, которые соответственно могут быть либо стимулом, либо ответом). Этот процесс продолжается до тех пор, пока не будет достигнут определенный критерий усвоения. Порядок элементов, воспроизводимых испытуемым в процессе заучивания, не соответствует действительному расположению этих элементов в ряду: некоторые из них появляются преждевременно (например, 8-й элемент ряда приводится перед 5-м), другие, напротив, с опозданием (например, 3-й элемент приводится после 7-го). Ошибки первого рода называются антероградными ассоциациями, а ошибки второго рода - ретроградными ассоциациями.

Для объяснения этого феномена была выдвинута гипотеза, согласно которой ответ на какой-либо элемент х ряда будет ассоциироваться в процессе заучивания с ответами на все другие элементы, которые предшествуют или следуют за элементом х и находятся от него на различном расстоянии. Эти гипотетические связи графически представлены на рис. 1.

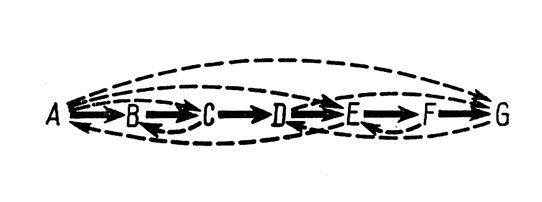
Рис.1. Гипотетическая схема смежных и 'дистантных' ассоциаций между элементами ряда (по Мак-Геч и Айриону, 1952, стр. 91)

Для изучения влияния таких "дистантных" ассоциаций на научение и память применялось несколько методов. Эббингауз (1885) применял метод "производных рядов". Заучивался ряд из 16 бессмысленных слогов, порядок расположения которых оставался постоянным (1, 2, 3, 4, 5, 6, . . ., 14, 15, 16); через 24 часа те же самые слоги заучивались вновь, но на этот раз они были расположены в другом порядке, который систематически от опыта к опыту изменялся. Например, Эббингауз располагал рядом слоги, которые в первоначальном ряду были отделены друг от друга одним (то есть: 1, 3, 5, 7, 9, 11, 13, 15, 2, 4, 6, 8, 10, 12, 14, 16), двумя (порядок: 1, 4, 7, 10, 13, 16, 2, 5, 8, 11, 14, 3, 6, 9, 12, 15), тремя или семью промежуточными слогами. Кроме того, в качестве контрольного вновь заучивался другой ряд, включавший в себя те же самые стимулы, расположенные в случайном порядке. Рабочая гипотеза состояла в утверждении, что если при первом заучивании образуются ассоциации первой ("перескакивающие" через один промежуточный слог), второй ("перескакивающие" через два промежуточных слога), п степени, то это приводит к более высокому сбережению упражнения, чем при случайном расположении элементов в ряду.

Результаты, полученные Эббингаузом (табл. I), показывают, что величина сбережения упражнения, достигнутая при заучивании производных рядов, уменьшается обратно пропорционально числу промежуточных слогов в производных рядах. Эта величина, таким образом, имеет тенденцию постепенно приближаться к величине сбережения в рядах элементов, расположенных в случайном порядке, где она практически равна нулю.

Таблица I

Однако метод производных рядов дает лишь косвенные сведения о наличии и роли "дистантных" ассоциаций. К тому же уменьшение величины сбережения в зависимости от увеличения расстояния между стимулами можно интерпретировать двумя различными способами, которые, однако, вовсе не исключают друг друга. При повторном заучивании отдаленные ассоциации будут менее эффективными, чем ассоциации более близкие, потому что: 1) они более слабые и 2) менее многочисленные.

Вслед за Эббингаузом выяснению этого вопроса способствовали другие исследователи, использовавшие метод ассоциаций (Вольгемут, 1913) (Этот метод для изучения рассматриваемой проблемы был введен именно Вольгемутом (1913), однако он интересовался лишь смежными антероградными и ретроградными ассоциациями). Ряд стимулов заучивается в определенном, заранее установленном порядке; после этого испытуемому предъявляют любой случайно выбранный стимул данного ряда и просят его быстро ответить первым пришедшим на ум элементом этого же ряда. В этом случае можно проверить, на каком расстоянии ив каком направлении по отношению к предъявляемому стимулу находится тот элемент ряда, который был назван в качестве ответа ( При этом методе во второй фазе эксперимента исключают первый (так как он не может вызвать ретроградные ассоциации) и последний (так как он не может вызвать антероградные ассоциации) стимулы первоначального ряда, однако испытуемый сохраняет возможность называть их в ответ на другие стимулы). Использование этого метода привело к установлению нескольких фактов.

1) Антероградные и ретроградные ассоциации охватывают, в сущности, все без исключения стимулы заучиваемого ряда независимо от расстояния между стимулами (Мак-Геч, 1936; Раскин и Кук, 1937; Хертцман и Нефф, 1939; Уилсон, 1943,1949). На табл. II представлены результаты, полученные Хертцманом и Неффом (1939) на четырех группах испытуемых, заучивавших по методу антиципации один и тот же ряд из 8 бессмысленных слогов до достижения различных уровней научения и избыточного научения (22 испытуемых I группы не имели ни одного безошибочного повторения; 27 испытуемых II группы достигли критерия 2-3 безошибочных повторений; 32 испытуемых III группы - критерия 4-6 безошибочных повторений и 26 испытуемых IV группы - 7-9 безошибочных повторений). Для проведения ассоциативного эксперимента был составлен ряд из 24 элементов, образованный из 8 первоначальных элементов, расположенных в случайном порядке, причем каждый из элементов повторялся 3 раза, однако таким образом, что одинаковые элементы никогда не оказывались рядом.

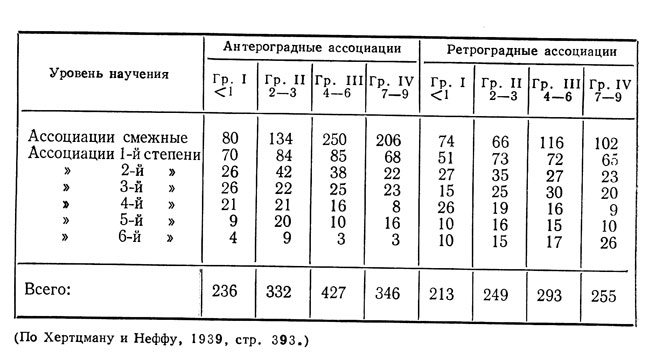
Таблица II. Зависимость антероградных и ретроградных ассоциаций от расстояния между стимулами и уровня научения

Если внутри каждой из четырех групп сравнить общее количество антероградных и ретроградных ассоциаций, то можно заметить, что при любом уровне научения антероградных ассоциаций значительно больше, чем ретроградных (236 и 213 для I группы, 332 и 249 для II группы и т. д.). Этот результат соответствует выводам других авторов (особенно Мак-Геч, 1936; Раскин и Кук, 1937).

2) Отмечается также, что смежные ассоциации, как правило, являются более многочисленными. Процент этих ассоциаций (определяемый по отношению к соответствующему общему числу антероградных или ретроградных ассоциаций) возрастает при повышении уровня научения, вызывая в то же время уменьшение числа отдаленных ассоциаций (соответствующих 1, 2, 3, 4, . . ., 6-й степени). Так, для самого низкого уровня научения, при котором еще не достигается критерий безошибочного воспроизведения (группа I), смежные антероградные ассоциации составляют лишь 33,9% общего количества антероградных ассоциаций (то есть 80/236 нако их процент увеличивается до 59,2 (то есть 206/346 ассоциаций), когда упражнение продолжается до достижения высокого критерия избыточного научения (группа IV). Эта закономерность оказывается сильнее выраженной для антероградных, нежели для ретроградных, ассоциаций.

3) Наконец, анализ всех количественных данных, приведенных в табл. II, свидетельствует о том, что, как правило, количество отдаленных ассоциаций уменьшается обратно пропорционально расстоянию. Однако этот эффект расстояния затушевывается, поскольку для ретроградных ассоциаций шестой степени (когда в ответ на последний стимул испытуемый называл первый стимул ряда) характерна особенность, которую отмечали уже Раскин и Кук (1937): цифры предпоследней строчки табл. II свидетельствуют, в сущности, о том, что эти ассоциации являются относительно более многочисленными по сравнению с соответствующими антероградны-ми ассоциациями и что наряду с этим наблюдается тенденция к увеличению их при повышении уровня научения (10, 15, 17, 26) до такой степени, что их количество превышает число отдаленных ассоциаций низшего порядка (см. последнюю колонку табл. II). Для объяснения этого феномена можно предположить, что при последовательных повторениях образуются антероградные ассоциации последнего стимула ряда с ближайшим к нему последующим стимулом, которым в данном случае является первый стимул того же ряда. Этот круговой эффект существенно усложняет проблему ассоциаций между внутренними элементами, так как, хотя он относится особенно к двум крайним стимулам ряда, он, разумеется, не ограничивается последними (Чтобы упростить изложение этого вопроса, мы ограничились анализом динамики первичных данных. В действительности, число отдаленных ассоциаций, фактически воспроизведенных испытуемыми, следует сравнить с общим количеством возможных отдаленных ассоциаций. Общее количество возможных ассоциаций неодинаково при различном расстоянии между стимулами. Например, все стимулы ряда 1, 2, 3, 4, 5 и 6-ой могут вызывать антероградные ассоциации первой степени (1->3; 2->4; . . .; 6->8); принимая во внимание, что в описанном выше эксперименте каждый стимул в ходе ассоциативного эксперимента предъявлялся три раза, общее количество возможных ассоциаций первой степени равно 6X3=18 для одного испытуемого я 18XN для N испытуемых. Напротив, антероградные ассоциации шестой степени могут вызываться лишь первым стимулом, по той же причине их возможное общее количество равно лишь 3XN. Из этого следует, что уменьшение отдаленных ассоциаций с увеличением расстояния между стимулами обусловлено отчасти уменьшением количества всех возможных ассоциаций. Хертцман и Нефф подсчитали процент отдаленных ассоциаций при любом расстоянии между стимулами по отношению к общему количеству возможных ассоциаций. Эти вычисления еще более отчетливо подтверждают существование кругового ассоциативного процесса, о котором мы говорили выше).

Б. Прогрессивное и регрессивное внутреннее торможение

Если заучиваемый материал состоит из элементов, расположенных в ряд, то элементы, находящиеся в начале и в конце, запоминаются быстрее, чем элементы, находящиеся в середине. Точнее, эмпирически установлено, что хуже всего запоминаются элементы, несколько смещенные от центра к концу ряда.

Это явление, отмеченное уже Эббингаузом (1885), было подтверждено многими психологами, в том числе Робинсоном и Брауном (1926), Фуко (1928), Лепли (1934), Уордом (1937) и Ховлэндом (1938а, 1938b). Его легко показать, если, используя метод антиципации, предложить группе испытуемых заучить ряд вербальных стимулов, а затем для последовательных периодов научения представить на кривой количество правильных антиципации стимулов, занимающих различные места в ряду, от 1-го до n-го (рис. 2).

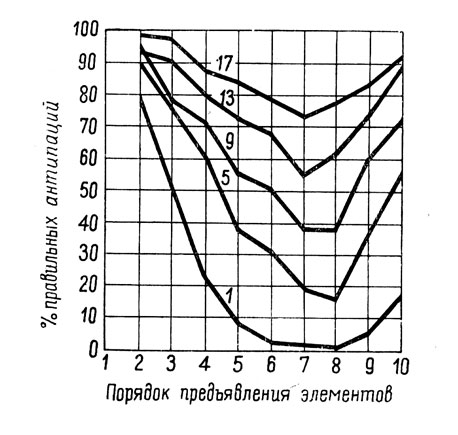
Рис. 2. Влияние положения элементов на запоминание ряда из 10 трехзначных чисел. Всего было 8 рядов и 11 испытуемых. Кривые, обозначенные цифрами 1, 5, 9, 13, 17, относятся соответственно к 1, 5, 9, 13 и 17 пробам. Каждая из точек, использовавшихся для построения этих кривых, обозначает процент правильных ответов при 8, 11 и 88 попытках антиципации следующего числа на основании предыдущего (по Робинсону и Брауну, 1926, стр. 547)

Согласно объяснению, предложенному Фуко (1928), это явление есть результат взаимодействия двух процессов торможения, одновременно действующих в ходе научения и замедляющих последнее. Первый процесс - прогрессивное внутреннее торможение - проявляется в том, что ответы на предыдущие стимулы оказывают интерферирующее влияние на ответы, относящиеся к последующим стимулам; второй процесс - регрессивное внутреннее торможение - проявляется в том, что ответы на последующие стимулы оказывают интерферирующее воздействие на ответы, относящиеся к предшествующим стимулам. Вытекающая из такого понимания гипотеза может быть сформулирована следующим образом: влияние прогрессивного или регрессивного внутреннего торможения на ответ, относящийся к данному стимулу, будет тем сильнее, чем больше число предшествующих стимулов в первом случае и последующих во втором.

Фуко (1928) проверил эту гипотезу в исследовании, в котором испытуемым (детям от 10 до 14 лет) предлагалось сразу же после одного предъявления воспроизвести ряды из 3, 4, 5, 6 и 7 слов. В таблице III приводятся данные о том, сколько раз испытуемые не могли воспроизвести первый (находящийся под воздействием лишь регрессивного торможения) и последний (находящийся под воздействием лишь прогрессивного торможения) стимулы указанных рядов. Изменение этих показателей в зависимости от числа стимулов в рядах, по-видимому, подтверждает рассматриваемую гипотезу.

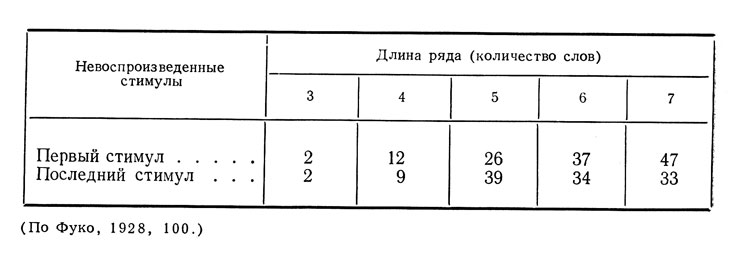
Таблица III. Влияние объема заучивания материала на забывание первого и последнего стимулов ряда

Другая гипотеза, предложенная Фуко, исходит из того, что прогрессивное торможение, ослабляя ответы, увеличивает тем самым подверженность этих ответов воздействию регрессивного торможения. Одновременное действие этих двух видов торможения на все ответы, относящиеся как к предшествующим, так и к последующим стимулам, вызывает общее торможение, гораздо более сильное, чем можно было бы ожидать от сложения этих видов торможения. Эта гипотеза подтверждается следующими фактами: если бы эти два вида торможения просто суммировались, то забывание 4-го элемента ряда, состоящего из 7 слов, должно было бы в таком случае равняться сумме числа забываний 1-го и 4-го элементов ряда, состоящего из 4 слов, поскольку в обоих случаях прогрессивное торможение вызывается воздействием 3 предшествующих по отношению к интересующему нас элементу слов, а регрессивное - воздействием 3 последующих слов. Однако в действительности четвертое слово ряда, состоящего из 7 элементов, было забыто 81 испытуемым из 100, тогда как первое и последнее слова ряда, состоящего из 4 элементов, были забыты, в общем, лишь 21 раз из 100 (12 испытуемых забыли первое слово ряда и 9 испытуемых - последнее). Совместное действие этих двух процессов торможения оказывается, таким образом, значительно более эффективным, чем можно было бы ожидать при простом суммировании этих процессов; этот факт позволяет понять, почему ответы на стимулы, расположенные в середине ряда, испытывают максимальное воздействие интерференции: здесь сильнее всего проявляется эффект взаимодействия прогрессивного и регрессивного торможения. Однако гипотеза Фуко лишь весьма приближенно отражает действительное положение вещей, поскольку, как уже указывалось, элемент, подверженный максимальному воздействию прогрессивного и регрессивного торможения, оказывается несколько смещенным от центра к концу ряда (Халл (1935) развивал гипотезу (сформулированную Лепли в 1934), которая пытается описать эти эффекты положения в ряду в понятиях обусловливания. Согласно этой гипотезе, каждый стимул ряда ассоциируется в ходе научения, по антероградному типу, с каждым из последующих стимулов посредством процесса, аналогичного процессу выработки следовых условных реакций. Каждая ассоциация характеризуется потенциалом возбуждения, способным вызвать ответ, и потенциалом торможения типа павловского запаздывающего торможения. Из этого следует, что если имеется ряд, состоящий из стимулов А, В, С, D, Е, . . ., N, то прямые ассоциации между А и В, В и С, С и D и т. д. будут благоприятствовать воспроизведению этих стимулов. Напротив, дистантные ассоциации между А и С, А и D, А и Е, А и N, В и D и т. д. будут тормозить воспроизведение находящихся между ними промежуточных стимулов. Вероятность воспроизведения какого-либо стимула будет в этом случае тем меньше, чем больше дистантных ассоциаций, которые "перекрывают" этот стимул. Однако эта гипотеза - изложенная зчесь лишь в общих чертах - не является более удовлетворительной, чем гип отеза Фуко, поскольку она также предполагает, что наиболее подверженным влиянию прогрессивного и регрессивного торможения является стимул, расположенный в центре ряда. Поэтому Халл и его сотрудники (1940) более строго пересмотрели свою объяснительную систему. Новая формулировка более адекватно объясняет эффекты, связанные с элементами внутри ряда; однако, помимо того что эта теория остается весьма гипотетической, она противоречит возможным предположениям о влиянии других феноменов этого же рода: например о влиянии распределения упражнения на эффективность научения. В этом отношении представляют интерес высказывания Осгуда (1953)).

Первые и последние элементы ряда оказываются в благоприятном положении также и при отсроченном воспроизведении. Кривая на рис. 3 показывает число правильных воспроизведений бессмысленных слогов в зависимости от положения слогов в ряду через 24 часа после заучивания, продолжавшегося до достижения критерия первого безошибочного воспроизведения (Андервуд и Ричардсон, 1956). Постман и Pay (1957) получили аналогичные результаты для интервалов в 24 и 48 часов, используя ряды английских слов. Причины этого долговременного эффекта, по всей вероятности, различны: с одной стороны, ответы на первый и последний стимулы лучше сохраняются ввиду того, что, запоминаясь первыми, они наиболее часто воспроизводятся испытуемыми в ходе научения; с другой стороны, ответы на стимулы, находящиеся в середине ряда, может быть, более чувствительны по сравнению с остальными к явлениям проактивной и ретроактивной интерференции (см. стр. 304 и далее), поскольку они являются менее устойчивыми и широко подвержены влиянию прогрессивного и регрессивного торможения.

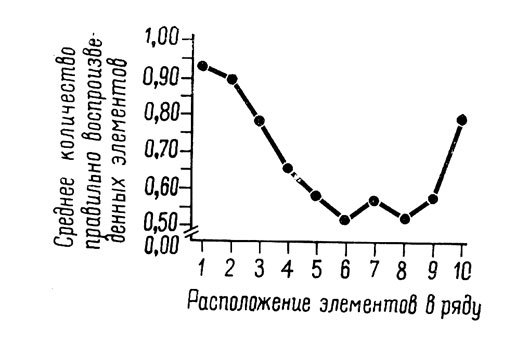
Рис. 3. Зависимость количества воспроизведенных элементов (средние данные) от расположения этих элементов в ряду (по Андервуду и Ричардсону, 1956, стр. 122)