Инженерная психология и теория информации

В любой публикации по инженерной психологии - будь то обстоятельный научный труд или небольшая статья в научно-популярном журнале- мы обязательно встретимся с термином "информация". Не раз употреблялся он и в этой книге. Иначе и быть не могло: ведь главный предмет инженерной психологии - это информационное взаимодействие в СЧМ.

В повседневной жизни под информацией подразумеваются различные сведения, которые люди передают друг другу. В инженерной психологии этот термин употребляется в более широком смысле. Во-первых, он включает также (и прежде всего) обмен сигналами между человеком и машиной или между самими машинами, во-вторых, использование понятия информации в инженерной психологии обязательно предполагает ту или иную форму ее измерения. И это, пожалуй, главное. В самом деле, как можно говорить об информационной загрузке (перегрузке, недогрузке и т. д.) оператора, не измерив тем или иным образом эту самую загрузку, не сопоставив результаты измерений с соответствующими нормативами? Понятие норматива тоже основано на определенных измерениях, в данном случае - на измерении способностей человека принимать, сохранять, воспроизводить, перерабатывать и передавать различные виды информации в разных условиях с различной скоростью.

Скажем сразу: проблема эта чрезвычайно сложная, многогранная. Хотя над ее решением вот уже свыше трех десятилетий упорно трудятся тысячи специалистов во многих странах мира, достижения в этой области пока сравнительно скромные. Но все же представить себе современную инженерную психологию без использования теории информации, пожалуй, невозможно.

Первым большим достижением в этой области была разработка понятия о единице информации. В 1948 г. американский инженер и математик Клод Шеннон предложил связать понятие информации с понятием о неопределенности ситуации: чем более неопределенную ситуацию можно сделать определенной при помощи данного количества информации, тем большим является это количество. Преимущество такого подхода было очевидным: ведь неопределенность ситуации люди научились измерять гораздо раньше, создав для этого специальную теорию - теорию вероятности. Неопределенность ситуации измеряется количеством равновероятных исходов, которые она допускает в отношении данного события.

Возьмем для примера положение, в котором может находиться тот или иной предмет. Так, хорошо известная всем детская игрушка ванька-встанька, какой бы стороной ее ни клали на стол, всегда занимает одно положение - вертикальное. Стало быть, исход этой ситуации является совершенно определенным. А вот при подбрасывании монетки уже существует известная неопределенность: монетка может упасть либо одной, либо другой стороной. Еще большая неопределенность существует при подбрасывании игральной фишки, имеющей кубическую форму: ведь она может лечь на любую из шести своих граней.

Сообщение о том, какое положение занял ванька-встанька, не содержит абсолютно никакой информации. Сообщение о том, какая сторона монеты ("герб" или "решетка") оказалась сверху после ее подбрасывания, содержит минимальное количество информации. И значительно большее количество информации несет в себе сообщение о том, какая цифра оказалась на верхней грани упавшей кубической фишки.

Исходя из такого рода рассуждений, К. Шеннон предложил специальную формулу для измерения количества информации, содержащейся в том или ином сообщении:

где: n - количество возможных исходов данной ситуации¹.

¹ (Для тех читателей, которые еще не знакомились с понятием логарифма, укажем, что данный термин означает показатель степени, в которую нужно возвести какое-либо определенное число (называемое основанием логарифма), чтобы получить данное число. Приведенная выше формула гласит поэтому: количество информации, которое содержится в сообщении об исходе данного события, равно двоичному логарифму числа возможных его исходов.)

Пользуясь этой формулой, легко подсчитать, что сообщение об исходе подбрасывания монетки содержит 1 единицу, а известие об исходе подбрасывания кубической фишки - 2,57 единиц (log₂6). Так как в приведенной выше формуле используется логарифм с основанием 2, то единицу измерения информации принято называть двоичной единицей (дв. ед.), или битом (от английских слов binary digit).

Следует отметить, что отдельное сообщение может лишь частично ликвидировать неопределенность той или иной ситуации. Содержащаяся в сообщении информация в этом случае будет пропорциональна степени сокращения неопределенности. Так, если сообщение о месяце, в котором родился тот или иной гражданин, содержит 3,58 дв. ед. информации (log₂ 12), то известие о том, что его день рождения относится к первому полугодию, сокращает эту неопределенность вдвое, и следовательно, содержит 1 дв. ед.; сообщение о том, что данный гражданин родился в первом квартале, снова сокращает неопределенность еще вдвое и приносит еще 1 дв. ед.; сообщение о том, что гражданин родился в третьем месяце года, сокращает неопределенность в три раза, то есть увеличивает информацию на 1,58 дв. ед.

Конечно, приведенные выше рассуждения являются справедливыми лишь при том условии, что все возможные исходы рассматриваемых событий являются равновероятными. Но так бывает далеко не всегда. Например, для железнодорожного диспетчера известие о том, что на соседней станции один из боковых путей занял грузовой поезд, содержит меньше информации, чем сообщение о том, что боковой путь занят пассажирским поездом. Почему? Да потому, что пассажирские поезда обычно занимают один из главных путей.

Чтобы понять, каким образом теория информации используется в инженерной психологии, представим себе, что нам нужно решить элементарную задачу по проектированию операторского пульта. Исходные условия следующие: на пульте имеются 16 кнопок для передачи командных сигналов; нажатие на каждую из них приводит в действие (или, наоборот, отключает) один из 16 управляемых объектов; следовательно, если оператор получает по каналам связи команды, на какую кнопку следует нажать в тот или иной момент, то это значит, что каждая такая команда содержит в себе 4 дв. ед. информации (log₂ 16). По условиям задачи, ни телеграфной, ни телефонной связью наш оператор не располагает; информацию о том, на какую кнопку следует нажать в данный момент, он должен получать только при помощи сравнительно простых электрических сигналов, причем длительность передачи отдельной управляющей команды не должна превышать 5 с. Какая же система сигнализации окажется в этих условиях наиболее экономичной и надежной?

Первое, что обычно приходит в голову при решении данной задачи, - пронумеровать все кнопки, установить на пульте одну лампочку и адресовать управляющие команды, соотнося количество коротких вспышек лампочки с порядковым номером данного объекта (кнопки). У этого решения есть определенные достоинства: техническая простота, надежность, экономичность. Оно напоминает применявшиеся в древности системы коммуникации, основанные на использовании сигнальных огней.

Но тут сразу же возникают сомнения. Во-первых, уж очень медленно будет работать такая система: для передачи команды на 16-й объект потребуется не 5 с, а гораздо больше. Во-вторых, надежность... Нет, на этот раз мы имеем в виду не техническую, а психологическую надежность. Надежность оператора. Что, если он собьется в счете? Скажем, лампочка зажжется 15 раз, а оператору покажется что вспышек было 14? Ведь ошибка в передаче команды может иметь самые неблагоприятные последствия. Да и оператора следует пожалеть: каково ему будет без конца считать вспышки лампочек?

Тогда, может быть, установить на пульте 16 сигнальных лампочек - по одной на каждую кнопку? Очень удобно было бы для оператора, не правда ли? Но тогда потребовались бы и 16 линий связи! Нет, в техническом отношении это чересчур громоздко...

Но существует ли вообще у нашей задачи оптимальное (то есть благоприятное со всех основных точек зрения) решение? Да, существует, и основано оно на использовании теории информации. Чтобы легко было понять, в чем такое решение состоит, обратимся к схеме, представленной на рис. 8. Мы видим здесь все 16 наших кнопок; они расположены в горизонтальный ряд и обозначены буквами алфавита. Этот ряд разделен на разные части, представляющие определенную систему: две большие части (восьмерки), затем четыре части (четверки), восемь частей (двойки) и шестнадцать частей (это, естественно, единицы). Каждому из этих классов соответствует одна лампочка; всего, стало быть, на нашем пульте четыре лампочки. Каждый передаваемый ими сигнал несет 1 дв. ед. информации, причем любая команда состоит из четырех сигналов (по одному сигналу от каждой лампочки). Все это, разумеется, вполне приемлемо с точки зрения как технической надежности, так и экономичности данной системы. Что же касается психологической надежности, то судите, пожалуйста, сами. Оператору ничего считать не нужно, он должен постоянно помнить лишь одно простое правило: при передаче любой команды последовательно зажигаются все лампочки сверху вниз, давая либо одну, либо две короткие вспышки; при этом одна вспышка указывает на левую, две вспышки на правую сторону данной пары.

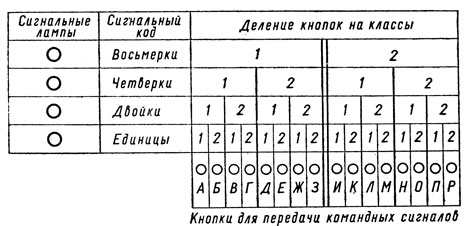
Рис. 8. Схема применения теории информации при конструировании элементарного пульта

Предположим, должна быть передана команда на нажатие кнопки "К" (10-й, если считать слева направо). Если разделить весь ряд на две равные части, то эта кнопка окажется во второй восьмерке: следовательно, самая верхняя лампочка (именно она обслуживает данный класс) должна дать две вспышки. Тем самым из заданного множества кнопок отсекается половина. Обратимся теперь к классу четверок: внутри второй восьмерки 10-я кнопка приходится на первую четверку, значит, вторая сверху лампочка должна дать одну вспышку: то же самое следует сказать и о третьей сверху лампочке, обслуживающей класс двоек. Наконец, поскольку внутри данной двойки 10-я кнопка занимает второе место, самая нижняя лампочка, "ответственная" за класс единиц, должна дать две вспышки. В целом команду на нажатие 10-й кнопки можно записать следующим образом: 2, 1, 1, 2.

У оператора, передающего команды на наш пульт, перед глазами может находиться простая табличка, содержащая такого рода сигнальные коды для всех 16 управляемых объектов: 1-й объект - 1, 1, 1, 1; 2-й объект - 1, 1, 1, 2 и т. д. С помощью этой таблички передавать команды на наш пульт совсем нетрудно. Да и быстрая, надежная расшифровка (чтение) принимаемых сигналов не составляет каких-либо проблем - просто требуется соответствующий умственный навык, который можно выработать в течение получасового упражнения.

Убедиться в этом может любой читатель, достаточно найти себе партнера по игре и, пользуясь приведенной выше таблицей, передавать друг другу закодированные сигналы для быстрой их расшифровки.

Раз речь зашла о кодировании информации, следует хотя бы вкратце остановиться на вопросе о физическом алфавите используемых сигналов. Смысл этого вопроса - в выборе определенных свойств тех физических объектов и процессов, которые, действуя на органы чувств человека, выступают для него в роли сигналов, несущих в себе ту или иную информацию.

Обратимся к спроектированному нами пульту. Здесь в роли сигналов выступает свет электрических лампочек, а их физический алфавит включает два свойства: относительное местоположение лампочек и количество даваемых ими вспышек. Это весьма простой и легко запоминающийся алфавит, состоящий всего из 8 сигналов (4 X 2).

Специалисты по инженерной психологии всегда стремятся пользоваться по возможности короткими и простыми алфавитами, состоящими из сигналов, легко отличимых как друг от друга, так и от разного рода посторонних помех. Одновременно они преследуют и другую цель: обеспечить как можно более емкое кодирование информации. При таком кодировании один сигнал несет в себе максимальное количество информации. Примером весьма эффективного кодирования информации могут служить аббревиатуры - разного рода сокращения, употребляемые как в письме, так и в устной речи. Современная речь насыщена большим количеством аббревиатур: НТР - научно-техническая революция, АСУ - автоматизированная система управления, ТЗ - техническое задание и т. п.

Получив возможность измерять передаваемую оператору информацию, инженерная психология стремится строго ограничить ее количество необходимым объемом. В соответствии с этим выделено два основных класса индикаторов.

Первый составляют индикаторы, показания которых содержат 1 дв. ед. информации. Это приборы-сигнализаторы. Они сообщают оператору, находится или не находится управляемый параметр системы в допустимых пределах. В последнем случае индикатор обычно передает сигнал предупреждения (красный свет лампочки, зуммер и т. п.). Когда шофер смотрит на индикатор количества бензина в баке, его в первую очередь интересует, не мигает ли красная лампочка. Если мигает, то это означает, что в баке остался минимум горючего, которого хватит, чтобы доехать до ближайшей автозаправочной станции. В любом случае данный индикатор всегда передает 1 дв. ед. информации.

Для передачи более точной количественной информации используются индикаторы второго типа: стрелочные, цифровые, телевизионные и др. Информационная емкость показаний таких индикаторов зависит от целого ряда факторов: цены деления шкалы, частоты и скорости изменения самих показаний, вероятности появления очередного сигнала и т. д.

Весьма эффективны индикаторы, представляющие собой своеобразную комбинацию этих двух типов. Такой индикатор изображен на рис. 9. Этот трехстрелочный индикатор отображает параметры работы авиационного двигателя: давление топлива, давление масла, его температуру. Казалось бы, что здесь особенного? Индикатор как индикатор. Но дело в том, что эти три стрелочных прибора (принадлежащих ко второму типу) скомпонованы таким образом, что в своей совокупности как бы составляют еще один - четвертый - индикатор (первого типа). Если три стрелки занимают такое положение, что вместе образуют перевернутую букву Т, это означает - все указанные параметры находятся в пределах нормы. Выходит, что пилот, воспринимая один знак, информацию получает не об одном, а о трех параметрах. Налицо тройная экономия времени восприятия.

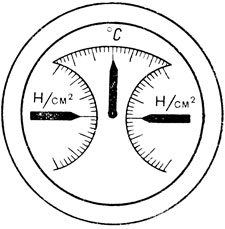
Рис. 9. Комбинированный авиационный индикатор

По принципу рационализации восприятия конструируются многие индикаторы, что значительно облегчает труд оператора.