О сходстве структур изображений (В. А. Ганзен, В. Ю. Мартишюс) [1975 - - Экспериментальная и прикладная психология. Выпуск 6]

Экспериментальные исследования опознания, различения, идентификации стимулов человеком приводят к необходимости введения мер сходства, близости объектов восприятия. Но такие понятия, как "сходство", "форма", весьма неопределенны. В связи с исследованиями в области распознавания образов были предприняты попытки формализовать понятие сходства. Нас интересуют такие меры сходства, которые адекватны восприятию человека.

Э. Зиман [1], Ю. А. Шрейдер [2] вместо понятия "сходство" предлагают аксиоматически определенное понятие "толерантность". Любое отношение толерантно, если оно симметрично и рефлексивно. Субъективное сходство должно удовлетворять свойствам симметричности и рефлексивности, но для содержательной психологической экспликэции понятия "сходство" этого явно недостаточно. В отношении толерантности находятся все объекты, имеющие общие признаки. Такое понимание сходства, например, оставляет вне рассмотрения его градации.

В каждодневной практике людей, как правило, наиболее похожими считаются те объекты, которые (при условии, что они не отличаются друг от друга второстепенными признаками) труднее всего различать наблюдателю. Под второстепенными, нерелевантными признаками подразумеваются те черты объектов, которые практически не влияют на оценку сходства. Грубо говоря, если для данного объекта изменить второстепенные признаки, то полученный новый объект должен быть почти так же похож на старый, как и точно ему идентичный.

Часто в исследованиях по автоматическому распознаванию образов сходство (близость) между изображениями выражается расстоянием в некотором метрическом пространстве. Расстояние между точками в любом метрическом пространстве должно удовлетворять условию треугольника. Но нет оснований полагать, что субъективное сходство удовлетворяет этому условию.

Допустим, что объекты x и y субъективно настолько же похожи друг на друга, насколько похожи y и z. Тогда из условия треугольника следует, что сходство между x и z не хуже определенной степени. Пусть мы устанавливаем степень сходства между отцом, сыном и матерью. Понятно, что может быть затруднительно ответить на вопрос: на кого более похож сын, на отца или на мать. Сходства же между отцом и матерью может не быть вообще.

В дальнейшем рассмотрении мы ограничимся двумерными контурными фигурами. Правомерно ставить вопрос о сходстве человеческих лиц, о сходстве почерков, о сходстве телосложения, словом, о сходстве между однородными объектами. Аналогично из огромного множества качественно различных контурных фигур сравнению по сходству формы подлежат только структурно однородные. Будем считать, что малая деформация фигуры оставляет ее качественно той же самой и что фигуры, состоящие из одинакового числа деталей, с тем же самым взаимным их расположением обладают одинаковой структурой. Ниже, исходя из этих допущений, мы предлагаем простой метод для определения структуры изображения.

Если метод определения структуры соответствует тому, который лежит в основе опознания изображений людьми, то фигуры, имеющие по этому методу одинаковую структуру, легко будут классифицироваться испытуемыми как принадлежащие к одному классу. Обратное утверждение, конечно, неверно. Ведь классификацию фигур можно провести не только на сходстве формы, но по другим признакам, например, логическим.

Пусть контурную фигуру пересекает семейство параллельных прямых. Определим порядок просмотра полосы как по направлению, параллельному прямым, так и по перпендикулярному им направлению, например, слева направо и сверху вниз. Пусть y=a - первая прямая, касающаяся фигуры (см. рисунок). Устанавливаем число точек, в которых прямая касается фигуры. Продолжая просмотр в указанном порядке, дойдем до первой прямой y=b, число пересечений которой с фигурой не совпадает с предыдущим числом касаний. Сосчитаем число пересечений. Дальше процедура аналогична. Там, где число пересечений меняется, сосчитаем их. Наконец, устанавливаем число касаний с другой стороны фигуры, если оно отличается от предыдущего числа пересечения.

Может случиться, что некоторые прямые совпадут с целыми отрезками контуров. Если следовать вышеуказанной процедуре, то число пересечений достигает бесконечности. Но если слегка деформировать фигуру, то можно избавиться от совпадений прямой с отрезком контурной фигуры и получить конечное число пересечений. Следовательно, метод не удовлетворяет предположению о том, что малая деформация фигуры не нарушает ее структуры. Поэтому необходимо сделать изменения в нашем правиле определения структуры изображения. Введем в рассмотрение квантовый уровень параллельности, т. е. будем считать все прямые, угол между которыми и данной прямой не превышает α, параллельными по уровню α.

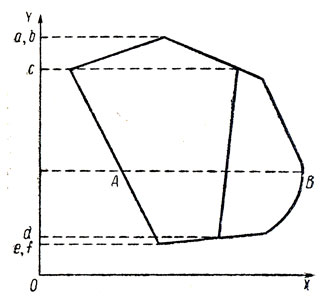
К процедуре описания структуры изображения. a - f - некоторые прямые из семейства параллельных, пересекающих изображение; a, f - граничные касательные прямые; b, c, d, e - прямые, разделяющие изображение области с различным числом пересечений параллельных прямых с контурами изображения

Через любую точку прямой можно провести бесконечное множество прямых, параллельных ей по данному квантовому уровню. Пусть A и B - крайние точки пересечения прямой из исходного семейства параллельных с контурами фигуры (см. рисунок). Если почти для всех точек отрезка AB, за исключением, может быть, конечного их числа, справедливо, что почти все параллельные по квантовому уровню а прямые пересекают контуры фигуры одинаковое число раз, то зафиксируем это число. В нашем случае это число равно 3. Если множество параллельных по данному квантовому уровню прямых распадается на несколько непустых подмножеств, внутри которых число пересечений прямых с контурами фигуры одинаково, а в разных подмножествах оно различно, то зафиксируем число пересечений для подмножества наибольшей меры.

Процедура установления структуры изображения выглядит следующим образом. Начинаем просмотр параллельных от прямой, непосредственно примыкающей к касательной. Для этой прямой по описанному выше правилу зафиксируем число. Продолжая просмотр фигуры, отмечаем то число, которое не совпадает с предыдущим. Просмотр оканчиваем прямой, непосредственно примыкающей к касательной с другой стороны фигуры.

Результаты проделанной процедуры можно представить в виде столбца структуры, где смежные числа обязательно различны. Если для нескольких изображений столбцы структуры совпадают, то по нашему методу все эти изображения имеют одинаковую структуру по определенному направлению, точнее, по одному квантовому направлению.

Чем меньше величина угла а, тем объективнее выражается структура изображения. Но, с другой стороны, чем меньше а, тем больше вероятность ошибки, т. е. преувеличение роли деталей изображения, фактически не влияющих на воспринимаемую людьми структуру изображений. К счастью, для многих знаков, например, букв алфавита, а может варьировать в достаточно широких пределах, не влияя на столбец структуры.

Для полного установления структуры изображения одного квантового направления недостаточно. Но для этого практически достаточно двух квантовых направлений, угол между которыми "близок к прямому. При двух направлениях столбцов структуры тоже две. Если они для некоторого изображения равны столбцам другого изображения по тем же самым направлениям, то структура изображений одинакова. Для каждой буквы русского или латинского алфавита, а также арабской цифры получается своя пара столбцов. Итак, пара столбцов может быть инструментом распознавания изображений букв и цифр.

Психологические эксперименты показывают, что ортогональные системы координат имеют особое положение среди множества возможных координатных систем [3]. Если испытуемый оценивает направление прямой, то он делает ошибку в сторону либо вертикального, либо горизонтального направления, в зависимости от близости этих направлений к истинной ориентации прямой. Если есть дополнительная прямая, то оценка отклоняется в сторону перпендикуляра к этой линии. Эти результаты тоже побуждают к выводу, что для установления структуры изображений лучше всего пользоваться двумя ортогональными направлениями.

В наиболее простых случаях для описания изображения достаточно одного направления. Например, для изображения, состоящего из пучка параллельных линий, достаточно по направлению, перпендикулярному прямым, вычислить длины отрезков между параллельными, чтобы однозначно описать изображение. Если испытуемому предъявить такой пучок прямых, то у него после этого возникает последовательный образ, также состоящий из пучка параллельных линий, но перпендикулярных к исходным [4].

Предлагаемый метод выявления структуры не инвариантен к повороту. Действительно, в общем случае только поворот фигуры на малый угол не изменит значения столбцов структуры. Величина угла, к которому инвариантность сохраняется, зависит от самой фигуры. Если допустить совместное вращение обоих семейств параллельных и направляющих осей просмотра изображения, то идентификация фигуры возможна независимо от степени поворота. Теперь получаем не два столбца структуры, а большее их количество. Если можно подобрать одинаковые пары столбцов для двух изображений, то они имеют одинаковую структуру. Заметим, что в действительности инвариантность узнавания к повороту как для животных, так и для людей только частична [5, 6].

Возможно, что в некоторых случаях в восприятии участвует не только декартова система координат, которая лежит в основе нашего метода, но и другие координатные системы, например, полярная. Но ив этом случае процедура установления структуры изображения проводится аналогично, только вместо прямоугольной развертки применяется радиальная.

По предлагаемому методу структура выражается глобально. Поэтому он явно непригоден для фигур с повторяющейся структурой, т. е. текстонов, по терминологии Ю. И. Лашкевича [7]. Сфера применения метода ограничивается фигурами-реонами.

Изображения, обладающие одинаковой структурой, сходны между собой. Для установления степени сходства между ними необходимо принять во внимание их метрические характеристики. Всю фигуру разделим на части, в пределах которых число пересечений одинаково. В точке пересечения граничных касательных к каждой части прикрепляем координатную систему, одна ось которой, например, x, ориентирована по направлению параллельных прямых, другая ось, y - перпендикулярно им. В каждой координатной системе масштаб по оси у выберем такой, чтобы координаты точек в каждой части менялись от 0 до 1. Аналогично поступаем и по отношению ко второму семейству параллельных прямых. Площади фигур, между которыми устанавливается сходство, нормируются к единице. Отрезки между смежными точками пересечения прямой с контурами фигуры обозначим l^ikm(y_k) где m - порядковый номер отрезка в множестве отрезков, расположенных на данной прямой, и k - порядковые номера семейства параллельных и координатной системы соответственно. Если число пересечений прямой семейства параллельных с контурами фигуры не согласуется с установленной структурой изображения, то вместо этой прямой необходимо рассматривать параллельную ей по данному квантовому уровню.

Величины l^ikm(y_k) могут служить инструментом опознания каждой индивидуальной замкнутой формы из множества сходных с нею с точностью до преобразования подобия. Если предварительно не нормировать площадь изображения, то каждому изображению соответствуют различные величины, l^ikm(y_k), за исключением некоторых зеркально подобных изображений.

Если в нашем методе установления структуры изображения не фиксировать направления развертки двумерного изображения, то изменением направления развертки на обратное можно добиться для любой зеркально подобной фигуры того же самого выражения для структуры. Отсюда следует, что идентифицировать зеркально симметричные фигуры по этому методу затруднительно. Отметим, что дети делают особенно много ошибок при опознавании подобных объектов [8].

где p и q - порядковые номера изображений. d_pq(y_k) тождественно равно нулю только для идентичных, одинаково ориентированных изображений, а также для некоторой части зеркально подобных (при фиксированном направлении развертки) фигур.

Однозначность описания изображения величинами l^ikm(y_k) позволяет надеяться, что формула сходства может быть выражена через эти величины.

Формула сходства должна удовлетворять отношениям симметричности и рефлексивности. Как уже было указано, для любых идентичных фигур d^ikm_pq (y_k) равно нулю. Кроме того, d^ikm_pq(y_k) симметрично по нижним индексам, т. е. d_pq=d_qp. Поэтому есть основание полагать, что формула сходства непосредственно выражается через d^ikm_pq(y_k). Трудность различия зеркально подобных изображений может служить этому подтверждением. Указать конкретный вид функции сходства без привлечения обширного экспериментального материала невозможно.

Указатель литературы

1. Зиман Э., Бьюнеман С. Толерантность пространства и мозг.- В кн.: На пути к теоретической биологии. М., 1970, с. 134-144.

2. Шрейдер Ю. А. Равенство, сходство, порядок. М., 1971, с. 73-113.

3. Bouma H., Andriessen J. J. Induced changes in the perceived orientation of line segments, - "Vision Res.", 1970, vol. 10, No 4, p. 37-43.

4. Mac Kay D. M. Visual noise as tool of research. - "J. Gen. Psychol.", vol. 72, p. 50-55.

5. Колере П. Некоторые психологические аспекты распознавания образов.- В кн.: Распознавание образов. М., 1970,, с. 16-87.

6. Sutherland N. S. Outlines of a theory of visual pattern recognition in animals and men.- "Proc. Roy. Soc. Ser. В", 1968, vol. 171, No 1024, p. 29-43.

7. Лашкевич Ю. И. О некоторых явлениях в зрительном анализаторе, связанных и распознаванием образов.- В кн.: Вопросы бионики. М., 1967, с. 48-,53.