4. Основные виды средних значении и их вычисление

Итак, измерение исследуемого в эксперименте признака дает нам выборку, или набор вариант, набор варьирующих значений признака. Каждая варианта в какой-то степени имеет право количественно представлять измеренный процесс в целом. Полные же сведения об этом процессе заключены во всей статистической совокупности, уже прошедшей свою первоначальную обработку, сведенной к той или иной кривой распределения (см. разд. 2, 3 этой главы).

Процесс последующей обработки эмпирического материала идет по пути дальнейшего свертывания информации. Ведь в статистическом распределении слишком много различных характеристик, а дальнейшая практическая работа, анализ и сопоставление различных выборок требуют уменьшения количества этих характеристик до некоторого минимального числа. Другими словами, требуется выявить систему параметров, т. е, тех немногих характеристик статистического распределения, которые в достаточной мере выражают общие свойства совокупности.

Выше указывалось, что для описания теоретических распределений имеется четкая и строгая система исчерпывающих параметров. Распределения эмпирические описываются аналогично, только сжатие информации на практике неизбежно означает и потерю ее части. Каждый параметр выборки - это лишь одна из ее характеристик, одна из фотографий исследуемого процесса, вовсе не исчерпывающая всей его картины. Система используемых параметров выборки должна охватывать максимум свойств исследуемого процесса в их комплексе. Всякий такой параметр (или критерий) должен быть четко осмыслен, т. е. требуется осознать, в каком именно направлении характеризует данный параметр всю выборку, сам измеренный процесс.

Среднее значение (центральное) - это некий обобщающий показатель положения и уровня центра распределения, т. е. того значения признака, вокруг которого концентрируются все другие варьирующие значения. Это очень важный и распространенный параметр выборки. В математической статистике есть довольно много видов средних величин. Каждая из них - это некоторая специфическая абстракция, за которой лежит вполне определенное содержание, своя специфическая смысловая нагрузка, что и делает среднюю величину определенным сплавом количественной и качественной оценки. Поэтому выбор формы средней - это выбор способа опосредствования данных, заключенных в полном объеме исходной выборки. Все последующие выводы несут на себе печать такого опосредствования, так или иначе отражают специфику выбранной средней величины и в этом смысле являются относительными. К тому же вопрос о выборе адекватной средней величины тесно переплетается с вопросом о форме статистического распределения и о необходимости соответствующего ее анализа.

Итак, основным, или определяющим, для каждого вида средней является качественное ее содержание, знание того, в каком смысле это средняя, в каких пределах идет усреднение- Именно в этом контексте будет идти наше дальнейшее рассмотрение основных видов средних значений, при этом умышленно будут избегаться теоретико-математические положения.

4-1. Средняя арифметическая величина соответствует формуле:

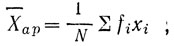
где x_i - значение варианты с номером от 1 до n,

f_i - частота соответствующей варианты,

N - объем выборки.

Для примера № 1 (данные табл. 2) имеем:

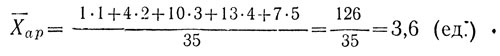
Для примера № 2 (данные табл. 1) имеем:

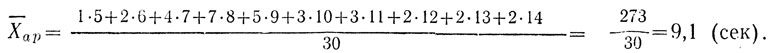
Средняя арифметическая - по своему определению (по формуле) предполагает суммирование всех исходных вариант и как бы равномерное распределение общего количества измеренного показателя между всеми вариантами (деление на N=Σf_i). Можно сказать, что в этой средней всегда присутствует некоторая скрытая оценка вала, т. е. суммы всех вариант исходной выборки (Xap•N=Σf_ix_i).

Средняя арифметическая несет в себе целый ряд математических преимуществ, ею удобно оперировать. Например, сумма отклонений всех вариант от нее равняется нулю (Σ(x_i-X_ap)=0), средняя арифметическая суммы (или разности) нескольких выборок равна сумме (или разности) средних арифметических значений этих выборок.

В практике измерений параметр X_ap чрезвычайно распространен, для всех привычен и, можно сказать, превратился в определенный стереотип при количественном анализе результатов (см. разд. 2 гл. I). Тем не менее смысл этого параметра отнюдь не так прост и очевиден.

Вернемся к нашим примерам № 1 и № 2. Что означает, скажем, величина X_ap=3,6 (ед.) для эксперимента по заучиванию двузначных чисел (работа № 10 гл. II)? Ведь ни один испытуемый не имел такого результата. По-видимому, наше X_apX_ap означает лишь то, что, если бы все 35 испытуемых запомнили именно 3,6 числа, их общая сумма (3,6 X 35) составила бы то же самое число, что и в опыте (126 двузначных чисел)... Осмысливанию параметра средней арифметической для конкретного рабочего измерения не слишком помогает и его механическая интерпретация, т. е. представление о параметре X_ap как о некой точке приложения равнодействующей всех сил (представленных в единицах f_i), формирующих данное статистическое распределение (центр тяжести фигуры, см. рис. 18).

Применяя параметр средней арифметической в обычном (и не слишком статистически представительном) измерении, мы, по-видимому, имеем в виду совсем другое среднее качество, т. е. то, которым параметр X_ap в данном случае не обладает вовсе. Исследователю хотелось бы назвать наиболее вероятное значение измеренного показателя, и здесь вступает в силу обозначенное ранее несоответствие понятий вероятность и типичность (см. разд. 2 гл. I). В самом деле, средняя арифметическая вовсе не обязательно указывает то значение признака, которое скорее всего будет получено при проведении еще одного, (n+1)-го измерения. Параметр средней арифметической является аналогом классического (теоретико-вероятностного) параметра математического ожидания: M=x_i•p_i. Но эта аналогия справедлива в предельном случае, когда N→∞,а

ω_i=f_i/N→p_i

При этом предполагается соблюдение принципа симметрии или взаимопогашение разносторонних отклонений от средней, а также соблюдение целого ряда указанных ранее допущений, обусловленных самой концепцией вероятностей (см. разд. 2 гл. I и разд. 1, 3 гл. III).

Так что в целом ряде практических случаев, при недостаточности объема выборки, а в особенности при наличии закономерной скошенности эмпирического распределения, некритическое использование параметра средней арифметической величины чревато серьезными ошибками в последующем содержательном анализе экспериментального материала (так называемые огульные средние).

4-2. Средняя геометрическая G определена следующей формулой:

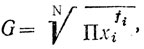
где x_i - величина каждой варианты,

f_i - частота варианты x_i,

П - знак произведений всех вариант.

Она вычисляется как корень степени N из произведений всех вариант исходной выборки.

Величина G для любой выборки меньше, чем величина средней арифметической.

Путем несложных математических преобразований удается показать, что средняя геометрическая может быть понята по смыслу как некое центральное или медианное значение в такой выборке, в которой варианты представляют собой геометрическую прогрессию, т. е. всякая последующая варианта равна предшествующей, умноженной на некий коэффициент прироста.

4-3. Средняя гармоническая Н вычисляется по формуле:

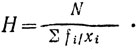
Это величина, аналогичная параметру средней арифметической. H - средняя, обратная средней арифметической, вычисленной не по исходному параметру x_i а по обратному ему параметру 1/x_i

Скажем, для нашего примера № 2 (см. разд. 2 гл. III) вычисление средней гармонической означает отыскание такой величины времени, которая исходит из предварительного вычисления некой средней скорости. Правда, подобная смена аргумента (проведенного уже измерения) отнюдь не всегда представляется нейтральным, чисто математическим приемом, отвечающим методике проведенного эксперимента. Тем не менее практика знает задачи, для которых применение параметра средней гармонической соответствует даже более, чем применение параметра обычной средней арифметической величины.

Величина H всегда меньше величины средней геометрической G. Следует сказать, что обе эти формы средних величин используются довольно редко как в элементарной статистике, так и в самой теории математической статистики.

4-4. Медиана M_e - это такое значение переменной, которое является срединным, центральным (по положению) в общем упорядоченном ряду вариант выборки. Медиана - это своеобразная золотая середина, справа и слева от которой остальные варианты располагаются поровну, тогда как их удельный вес, т. е. абсолютная величина каждой, как бы не принимается во внимание. Итак, M_e является величиной по смыслу срединной, центральной, она по происхождению прежде всего качественна, т. е. исходит не из аналитического выражения.

Воспроизведем табл. для нашего примера № 1, добавив к ней столбец Σf_i накопленных частот, т. е. сумму всех предшествующих вариант выборки плюс данная f_i

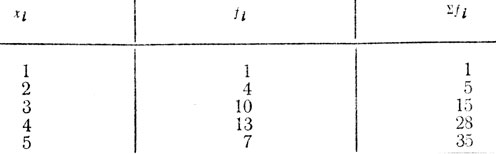
Таблица 3

Срединная варианта, т. е. такая, справа и слева от которой располагается равное количество вариант, имеет порядковый номер 18 (ведь общее N=35). Ее величина равна 4. Однако практика элементарной статистики предполагает более точное вычисление медианы, основанное на операции простейшей интерполяции. Для нашего примера медианный класс (разряд) x_Me=4, и таких вариант 13, т. е. f_Me=13. Использование приема интерполяции предполагает некоторый непрерывный рост вариант в каждом разряде, что особенно проблематично, конечно, для дискретных мер памяти, подобных нашему примеру № 1.

Вводим формулу интерполяции:

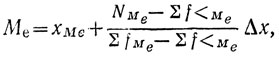
где

Δx - величина медианного разряда (в нашем примере = 1);

x_Me - начало медианного разряда (что для данного примера равно 4, так как это разряд точечный, дискретный);

N_Me - порядковый номер медианной варианты, равный 18;

Σf<M_e - накопленные частоты для разряда, являющегося меньше разряда медианного, т. е. для нашего примера равно 15;

Σf_Me-Σf<>_Me=f_Me - частота медианного разряда, или разность между накопленными частотами для разряда медианного и разряда меньшего, чем медианный, т. е.

Σf_Me-Σf<>_Me=28-15=13

Тогда M_e=4+ 18-15/28-15≈4,2

Аналогичным образом преобразовывается табл. 1 для примера № 2.

Таблица 4

В данном случае нет истинно медианного значения (четное число вариант, N=30), тогда за медиану принято брать среднее арифметическое значение между вариантами с номером N/2 и номером N/2+1, т. е. Это как бы варианта с номером 15,5,

Применяем сразу формулу интерполяции:

M_e=8,5+1 15,5-14/19-14=8,8

Медиана легче вычисляется, чем средняя арифметическая, поэтому может использоваться как заменитель X_ap (рабочий "суррогат"), В целом ряде практических случаев использование параметра M_e даже более предпочтительно: она менее подвержена влияниям случайных (в особенности крайних) колебаний вариант, выгодна в случаях неточностей концов распределения. Абсолютное отклонение значений вариант выборки от величины медианы является наименьшим по сравнению с отклонениями от других форм средней величины. Но с медианой невозможно использование удобных статистических критериев, основанных на сложении.

Медиана совпадает со средней арифметической только в случае распределения симметричного.

Теоретически медиана выступает как некая обобщающая ("истинная") средняя характеристика умеренно скошенного распределения, точнее, распределения логнормального, т. е. такого, которое подчинено нормальному закону при логарифме аргумента и в котором эффект действия каждого случайного фактора пропорционален уже достигнутому значению исследуемого признака.

В целом медиана как параметр средней величины находит достаточно широкое распространение для скошенных распределений, например, в психофизиологии или в психофизике при определении порогов чувствительности (см. работу № 1 в гл. II).

4-5. Мода M₀ - это значение варианты, наиболее часто встречающееся в выборке. Мода указывает наиболее типичное значение статистического признака и представляет особый интерес в распределении асимметричном, где вокруг значения моды концентрируются наибольшие частоты выборки. Мода есть некоторое среднее сгущение вариант, она обозначает место и величину воздействия наиболее сильного фактора среди всех тех, что формируют статистическую совокупность, дают проявление исследуемого признака. Мода - это некий класс наибольшего свойства, отнесенного к конкретным условиям измерения.

Параметр моды незаменим для шкалы наименований, т. е. в случае сугубо качественной градации вариант. Но мода удобна и для всех других шкал измерения, особенно для случаев большой вариативности показателя, для распределений многовершинных, где мода есть как бы выразительница типа.

Эмпирическое определение (вычисление) параметра моды, подобно вычислению медианы, основано на формуле простейшей интерполяции:

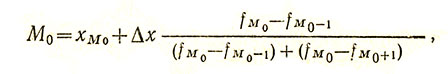
где xM₀ - начало модального, т. е. наиболее частого разряда или интервала;

Δx - величина, или ширина, модального разряда;

fM₀ - частота модального разряда;

fM₀-1 - частота разряда, смежного модальному слева, т, е. меньшего, чем xM₀

fM₀+1 - частота разряда, смежного модальному справа.

Вычислим M₀ для примера № 1 (исходя из табл. 2):

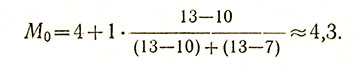
Значение моды для примера № 2 (по данным табл. 1):

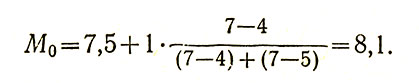
Помимо такого эмпирического (т. е. основанного на результатах конкретного измерения) вычисления, существует также вычисление, основанное на теоретическом определении моды как точки, соответствующей максимуму кривой распределения. При этом к эмпирическому распределению подбирается одна из наиболее соответствующих теоретических кривых распределения (например, набор кривых К. Пирсона), а затем параметр моды вычисляется аналитически, т. е. исходя из известной формулы той или иной подобранной теоретической кривой. Этот путь вычисления является математически громоздким и используется лишь в специальных исследовательских задачах.

Величина моды скошенного распределения отличается от величины медианы и величины средней арифметической- Интересно, что для умеренно скошенных эмпирических распределений (см. рис. 18) с достаточной точностью соблюдается известное соотношение К. Пирсона: M0≈X_ap-3(X_ap-M_e), т. е. медиана всегда располагается между величинами X_ap и M₀, причем ее удаленность от средней арифметической равна приблизительно ¹/₃ от общей разности между X_ap и величиной моды. Так что данное соотношение (правило Пирсона) может быть использовано для сглаживания эмпирических величин моды, которые, как правило, отличаются значительным непостоянством (по сравнению с величинами X_ap).

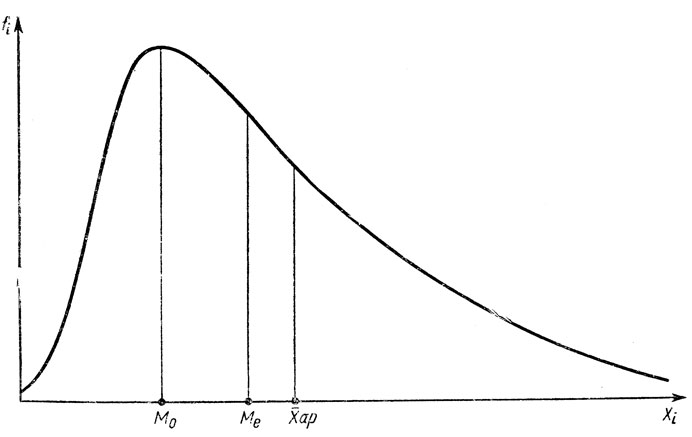
Рис. 18. Соотношение величин трех основных видов средней в умеренно скошенном распределении

Таким образом, для наших примеров № 1 и 2 получены следующие величины для трех важнейших видов средней:

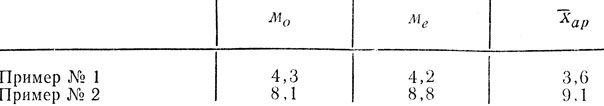
Таблица 5

Для распределения примера № 1 мы имеем так называемую левостороннюю (или отрицательную) асимметрию (см. рис. 15), распределение результатов в примере № 2 имеют скошенность положительную, или правостороннюю (такую же, как на рис. 18, см. также рис. 16).

Расхождение трех основных видов средней величины в скошенном статистическом распределении особенно четко ставит вопрос о качественном содержании усреднения, заключенного в каждой средней величине. В конкретном психологическом измерении здесь всегда имеется предмет для необходимого анализа. Для ситуации измерения эффективности некоей деятельности (подобной примеру № 2 по работе № 14, гл. II) может быть предложена такая модель отражательных характеристик трех средних значений: M₀ дает меру некоторой чистой, или потенциальной, обученности по данной деятельности; Мс измеряет реальный, отнесенный к конкретной ситуации навык, т. е. некоторую адаптированную обученность; X_ap может быть понята как мера общей успешности выполняемого действия, в котором навык зашумлен многими неспецифическими помехами. Тогда последующее симметричное распределение, в котором три этих параметра соединяются в одной точке, может быть понято как проявление некоторой предельной тренированности: навык полностью реализуется в деятельности и предопределяет ее конечную эффективность (M_e=X_ap), т. е. сливаются уровни навыка и натренированности, а уровень обученности более не маскируется недостаточностью адаптации к условиям (M₀=M_e).