5. Меры рассеяния (вариации, разброса) вариант

Разброс вариант по амплитуде вокруг среднего значения может иметь несколько показателей. Меры рассеяния оценивают степень изменчивости вариант, являясь одной из характеристик их группировки.

Например, кривые 1, 2 и 3 на рис. 19 отображают статистические распределения с равными средними значениями, но существенно различающиеся уровнем разброса значений. Для распределения по кривой 3 этот разброс наибольший, для кривой 1 - наименьший.

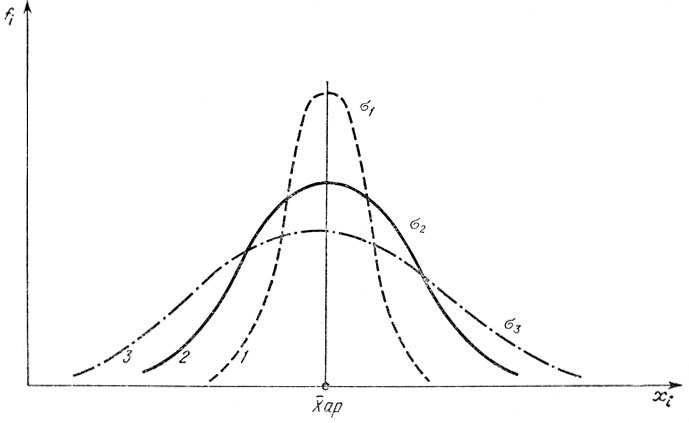
Рис. 19. Кривые распределения с равным средним значением X_ap, но отличающиеся степенью разброса вариант (σ₃>σ₂>σ₁)

5-1. Простейшей мерой рассеяния является вариационный размах, или разность между наибольшей и наименьшей вариантами, которую для обобщения можно выразить и в процентах, например, к среднему значению.

Для наших примеров № 1, 2 (по данным табл. 2 и 1):

Таблица 6

5-2. Среднее линейное (абсолютное) отклонение вычисляется по формуле:

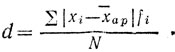
Вычисления по этой формуле целесообразно вести в специальной таблице. Проиллюстрируем это для наших примеров

Пример №1

Таблица 7

Пример №2

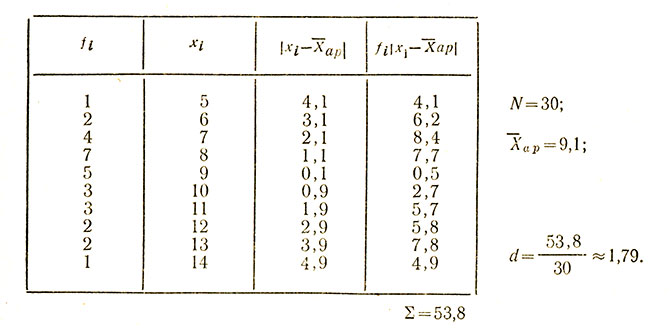
Таблица 8

5-3. Среднее квартильное отклонение (или семиинтерквартильный размах) - это мера разброса в распределениях, которые имеют параметром средней величины медиану. Квартальное отклонение Q - это половина расстояния между двумя квартилями: верхним Q_в и нижним Q_н т е. Q=Q_в-Q_н/2.

Известно, что медиана делит выборку на две равные по количеству вариант части (половины). Верхний квартиль Q_в - это медиана половины выборки со значениями больше медианы, нижний квартиль Q_н - это медиана другой половины выборки. Посчитаем квартили и квартильное отклонение для примера № 1 (удобнее работать с упорядоченной выборкой на с. 101 или данными табл. 3 на с. 113), применяя сразу формулу интерполяционного вычисления (см. разд. 4 о медиане):

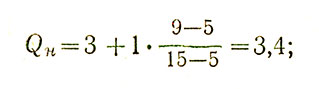
5-4. Среднее квадратическое отклонение (ошибка), или стандартное отклонение а, вычисляется по следующей формуле:

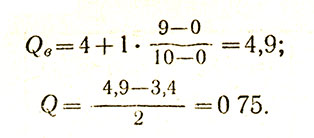
Причем деление (под радикалом) не на объем выборки, а на величину (N-1) является некоторой практической поправкой для измерений не слишком репрезентативных (N<100).

Стандартное отклонение является классической мерой разброса симметричного распределения. Величина D=σ² носит название дисперсии (флуктуации, девиаты). Чем больше дисперсия, тем больше разброс данных, как, например, для кривых на рис. 19 D₃>D₂>D₁ где индексы соответствуют номеру кривой.

Пример № 1 (по данным табл. 3)

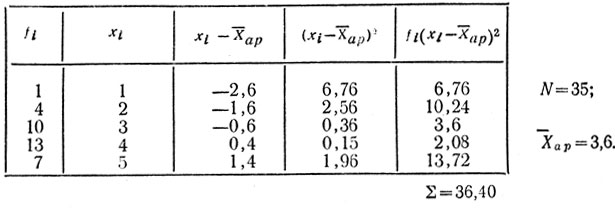
Таблица 9

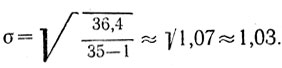
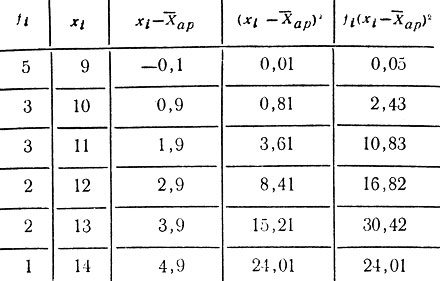
Пример 2 (по данным табл. 4)

Таблица 10

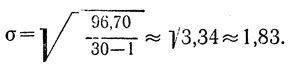
5-5. Коэффициент вариации V - это выраженное в процентах отношение стандартного отклонения к среднему арифметическому значению. Значит, эта мера дает возможность сравнить в абсолютных единицах вариативность выборок независимо от их среднего значения.

Для наших примеров № 1 и 2 имеем:

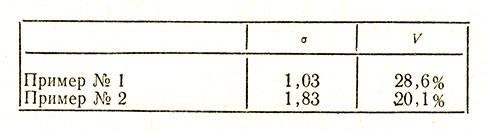
Таблица 11

Пример № 1 Пример № 2 1,03