3. Понятие о кривой распределения. Форма распределения, основные теоретические (классические) распределения

Кривая распределения - это предел, к которому стремится полигон частот при неограниченном увеличении объема статистической совокупности и уменьшении интервалов (увеличение точности измерения, переход от дискретной величины к непрерывной). Она дает характеристику некоторой генеральной совокупности, т. е. получаемые в эксперименте выборки лишь в той или иной степени приближаются к своему теоретическому пределу. Кривая распределения позволяет наглядно представить форму распределения, т. е. определенную закономерность специфической концентрации вариант в цельной статистической совокупности. Форма распределения является некоторой обобщенной характеристикой выборки: ведь исследуемая статистическая закономерность проявляется не только в обозначении среднего уровня измеренного процесса, но и в регуляции отклонений от этого уровня, т. е. в обозначении формы статистического распределения.

Все бесконечное разнообразие эмпирических кривых распределения (вне связи с теоретико-вероятностными построениями) принято делить на две большие группы: одновершинные и многовершинные (см. рис. 17, а). Последние называются также составными распределениями, т. е. являются следствием совместного графического представления различных (качественно разнородных) статистических совокупностей, в образовании которых преобладают какие-то различные закономерности.

Одновершинные распределения в свою очередь делятся на следующие группы:

а) симметричные (см. рис. 17, б), т. е. такие, в которых идет равновероятное уменьшение величины признака по обе стороны от некоторого и максимально частого значения; примером таких, сравнительно редко встречающихся в практике распределений является расположение людей по величине роста;

б) умеренно асимметричные или скошенные (см. рис. 17, в), в которых убывание числовых значений переменной в одну из сторон выражено заметно сильнее; таковы, например, распределения подавляющего большинства измерений эффективности человеческой деятельности;

в) распределения крайне асимметричные (см. рис. 17, г), характерные, например, для распределения населения капиталистических стран по величине материальной обеспеченности;

г) U-образные (см. рис. 17, д), в которых наибольшая частота свойственна обоим крайним значениям признака, например распределение облачности в районе Гринвичского меридиана.

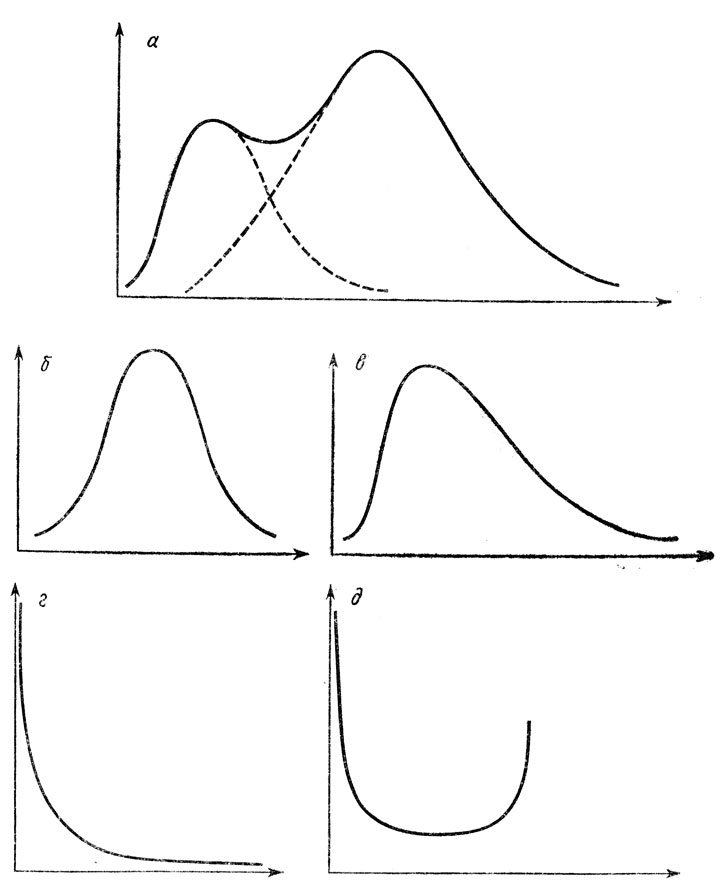
Рис. 17. Основные эмпирические типы форм распределения: а - многоверные; б - симметричные; в - умеренно скошенные; г - крайне асимметричные, д - U-образные

Таким образом, мы убеждаемся в большой показательности формы статистического распределения и в необходимости ее последующего рассмотрения при анализе полученных результатов.

Закон распределения - математическое соотношение, устанавливающее связь между возможными значениями варианты и соответствующими им вероятностями. Дать закон распределения случайной величины - это значит свести эмпирическую совокупность к тому теоретико-вероятностному закону, которому она более всего подчиняется. Закон распределения может быть задан:

а) таблицей или рядом распределения, в котором каждому значению x_i поставлена в соответствие его вероятность P_i,

б) многоугольником распределения (полигоном частот);

в) функцией распределения - аналитическим выражением (формулой), по которому может быть установлена вероятность каждого текущего значения случайной величины.

Теоретически (т. е. исходя из позиций чисто вероятностных) выделяют три важнейших типа распределений, которые называют часто классическими: биномиальное, нормальное (или распределение Гаусса) и распределение Пуассона.

Биномиальное распределение - это математическая модель ситуации, подобной той, что описывает классические игры вероятностей, типа подсчета односторонних выпаданий монеты или граней игральной кости при их идеальном подбрасывании.

Здесь все испытания независимы, вероятности всех событий равны и в сумме составляют единицу. Тогда вероятность P_n(m), т. е. вероятность осуществления m раз некоторого события А в серии испытаний n (общее число всех событий), описывается как последовательные члены разложения бинома n(q+p)^m, где p - вероятность наступления одиночного события А (например, это ¹/₂ для выпадания орла при подбрасывании идеальной монеты), q - вероятность события, противоположного событию А, или вероятность неосуществления события A (q=1-p).

Так что итоговая формула биномиального закона распределения имеет вид:

P_n(m)=C^m_n p^mq^n-m

где C^m_n - есть число сочетаний из n по m, т. е.

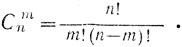
Биномиальное распределение полностью описывается (математически определено) двумя параметрами (показателями): n и p, так как его среднее значение M=np, а мера разброса значений (среднее квадратическое отклонение) σ=√npq.

Форма биномиального распределения существенно зависит от величин n и p, приближаясь в общем случае к симметричному распределению (см. рис. 17, б).

Нормальное (гауссово) распределение - это один из предельных случаев распределения биномиального, имеющий место при неограниченном увеличении числа испытаний (n→∞). При этом должно соблюдаться и такое общее условие, чтобы величина (q-p) была малой по сравнению с величиной √npq.

Исходя из теории ошибок Гаусса (из центральной предельной теоремы), распределение может считаться нормальным при условии достаточно большого числа независимых случайных величин, ни одна из которых не доминирует над другими ни по вероятности, ни по силе воздействия на общую сумму случайных величин. Именно эта сумма подчиняется тогда нормальному закону распределения, а вероятности и воздействия всех составляющих факторов есть величины бесконечно малые.

Нормальное распределение есть некоторая идеальная (колоколообразная) форма симметричного распределения (см. рис. 20). Его аналитическое выражение имеет вид:

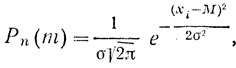
где известные математические постоянные π≈ 3,14, e≈2,72.

Значит, нормальное распределение также описано двумя параметрами: средним значением (математическим ожиданием) M (см. разд. 4 данной главы) и средним квадратическим отклонением о (см. разд. 5 данной главы). Поскольку само понятие гауссового распределения является предельным, математическое описание эмпирических распределений (принимаемых за нормальное) требует еще добавления параметра N, что характеризует репрезентативность статистической совокупности.

Когда при обработке экспериментального статистического материала встает задача установления формы полученного распределения, т. е. сведения его к одной из теоретических форм, то чаще всего предполагается, что измеренные показатели подчинены закону Гаусса. Нормальное распределение является наиболее изученным теоретически, имеет ряд чисто математических удобств, к нему отнесены многие мощные приемы и методы анализа. Разработаны даже специальные средства для преобразования эмпирических данных в нормальное распределение (подбор задач и условий эксперимента, смена аргумента, нормализация выборки по составу).

Математические преимущества закона Гаусса бесспорны, однако не только они должны приниматься во внимание при анализе результатов измерения. Предположение нормальности эмпирического распределения необходимо обосновывать качественно, осознавая все те допущения, о которых говорилось выше и которые сопутствуют теоретическому нормальному закону. Ведь всего удобнее было бы предполагать, например, некоторое точечное постоянство исследуемого в эксперименте показателя, т. е. исходить из полного отсутствия статистического распределения вообще. Так что весь вопрос выбора методики обработки заключается не просто в уровне математических удобств, а в степени соответствия той или иной математической модели теории реального процесса. Известно, что абсолютного соответствия здесь быть не может, поэтому речь идет всегда о "весе" тех неизбежных потерь сведений об изучаемом процессе, которые проистекают от математического (в данном случае статистического, вероятностного) его моделирования. Злоупотребления же безосновательными предположениями нормального закона распределения характерны отнюдь не только для психологии и подвергаются обоснованной критике.

Распределение Пуассона также исходит из биномиального распределения, когда величина одной из вероятностей p→0 т. е. становится бесконечно малой, а число испытания n→∞, т. е. неограниченно возрастает. В таком случае произведение np→λ; или стремится к некоторой малой, отличной от нуля величине кλ. Тогда вероятность P(m) того, что в последовательности из n независимых испытаний некое редкое событие А с вероятностью P(A)→0 осуществится m раз, определена формулой:

Значит, распределение Пуассона полностью описывается одним параметром λ, который характеризует и среднее значение распределения, и меру разброса случайных значений.

Близким к этому закону является, например, статистическое распределение числа военнослужащих конных войск, погибших под копытами лошадей. При этом редкие события как бы уходят из класса событий слепого случая, приобретают вероятностное толкование.

Форма распределения Пуассона также существенно варьирует от крайней асимметрии к симметрии (в зависимости от величины λ).