6. Некоторые другие параметры статистического распределения

При рассмотрении классических распределений (см. разд. 3 гл. III) указывалось, что каждое из них математически описывается своей системой параметров, которая всегда сводима к двум исходным: среднему значению и стандартному отклонению. Однако при описании эмпирических распределений зачастую необходимо введение дополнительных параметров, наиболее распространенными из которых являются коэффициент асимметрий и показатель эксцесса.

Коэффициент асимметрии А дает численную меру скошенности статистических распределений и вычисляется по формуле:

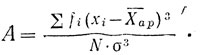
Для распределений симметричных этот коэффициент равен нулю, значение А положительно при правосторонней скошенности и отрицательно - при левосторонней.

Эксцесс E - это количественная мера "горбатости" симметричного распределения, т. е. некоторой плавности (крутости, остро- или туповершинности) верхней части распределения:

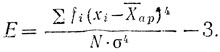
Величина эксцесса в нормальном распределении равняется нулю, при положительном значении E кривые называются островершинными, при отрицательном - туповершинными.

Значения коэффициентов A и E (в зависимости от объема распределения N и от уровня значимости (см. ниже), при которых данное эмпирическое распределение еще может считаться нормальным (или просто симметричным), даются в специальных статистических таблицах, имеющихся в соответствующих учебниках.