7. Понятие об уровне значимости

Всякий результат, полученный статистическим методом, относителен, а значит, относителен и вывод на основании этого результата. Такая относительность исходит из самой философии и методологии статистического исследования (см. разд. 1 гл. III), наконец, из того, что на основании некоторого вполне конечного числа наблюдений (объема выборки N) мы делаем выводы о некоторой генеральной совокупности (в которой N->∞). Конечно, закономерности, выявляемые в статистическом измерении, есть сами по себе факты, но науке всегда нужны более глубокие обобщения, нужна уверенность в определенной повторяемости закономерностей.

Исходя из этого, всякое утверждение, всякая цифра, полученные методами математической статистики, непременно должны быть обоснованы с точки зрения их достоверности. Последнее исходит из понятия математической вероятности (см. разд. 1 гл. III). Достоверно то, что описывается тем или иным законом распределения вероятностей, при этом более всего разработан и популярен (как указывалось ранее в данной главе) нормальный закон распределения.

Итак, всякое утверждение (статистическая гипотеза) характеризуется количественной мерой вероятности ее справедливости, реальности. Другой стороной этой характеристики выступает уровень значимости (существенности), под которым понимается вероятность отвергания гипотезы в случае ее справедливости.

Поясним это на примере нормального закона распределения (рис. 20). Площадь под нормальной кривой (или общий объем статистической совокупности) с данными параметрами может быть точно представлена и описана.

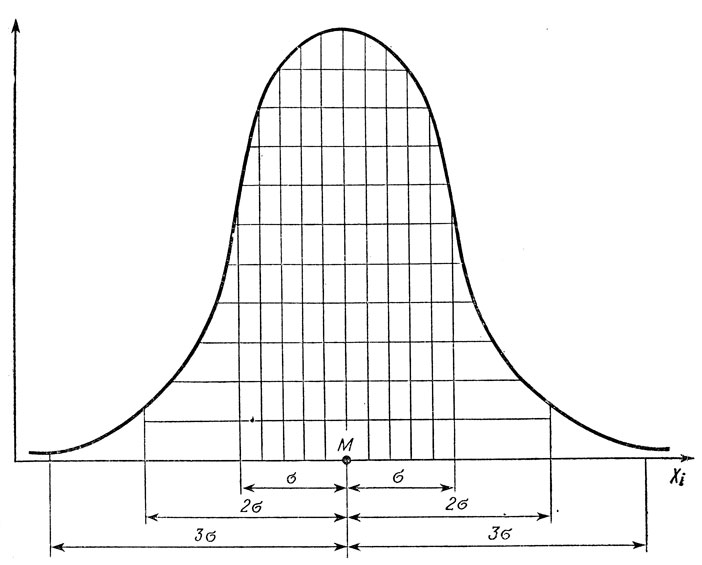
Рис. 20. Схематическое изображение нормальной кривой распределения и доверительных уровней (вероятностей попадания варианты в границы доверительного интервала M±кσ

Положим, на рис. 20 представлена некая генеральная совокупность с параметрами M и σ. Из теории известно, что значения вариант в пределах M±σ т. е. от варианты величиной (M-σ) до варианты (M+σ), составят точно 68,3% всех наблюдений, или 0,683 всей площади под нормальной кривой. Интересно, что именно в точках (M+σ) и (M-σ) нормальная кривая имеет наибольший наклон к оси абсцисс. Допустим, что распределение на рис. 20 - это распределение людей по величине роста, где M=168 см, а σ=6 см. Тогда сказанное выше означает: если мы спросим каждого человека о величине его роста, то окажется, что рост 68,3% людей будет в пределах 162-174 см (M±σ). Если мы перед этим утверждали, что все люди имеют рост между 162 и 174 см, то вероятность такого утверждения равна 0,683, а уровень значимости составляет 0,317 (=1-0,683). Величина же (M±σ) будет в данном случае границей доверительного интервала, или интервала уровня значимости.

Обобщим сказанное для некоторых величин уровня значимости, наиболее распространенных на практике.

Таблица 12

Итак, чем шире выбран интервал уровня значимости или чем меньше абсолютная величина уровня значимости, тем более строгим является утверждение данной статистической гипотезы, тем достовернее суждение и меньшее количество явлений относится нами в категорию случайных. Если речь идет о проверке значимости различий между статистическими параметрами (средние значения, показатели формы распределения и т. д.),то достоверными признаются только те различия (отклонения), которые выходят за пределы принятого интервала уровня значимости.

В практике статистических измерений наиболее распространены два уровня - пятипроцентный P_0,05 и однопроцентный P_0,01 (см. табл. 12). Принято считать различия достоверными, если уровень значимости меньше одного процента, т. е. если Р<0,01. Если величина вероятности ошибки данной гипотезы находится между пяти- и однопроцентным уровнями 0,05>P≥0,01, то факт проверяемого различия сомнителен, другими словами, тождества нет, но и различия еще не доказаны достоверно, нет убеждения в их существенности (значимости). Если же P≥0,05, то факт отсутствия реальных различий между сопоставляемыми величинами следует считать полностью доказанным статистически.

Это общее правило проверки результатов на статистическую значимость неоднократно иллюстрируется в последующих параграфах данной главы.