8. Проверка принадлежности крайних членов к данной статистической совокупности

Возможны выборки, в которых даже при беглом рассмотрении вариант выделяются некоторые крайние (много меньшие или много большие всех остальных) варианты, которые сомнительны как значения данной (качественно однородной) выборки. Математическая статистика располагает приемами проверки таких сомнительных крайних членов на их принадлежность к совокупности.

8-1. Простейшим приемом такой проверки, основанном на предположении нормальности эмпирического распределения, является τ-критерий (тау-критерий):

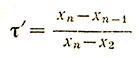
- для проверки последней варианты (с номером n), если она сомнительна;

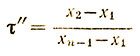
- для проверки первой варианты (с номером 1),

где все индексы при x означают порядковый номер варианты в их упорядоченном ряду.

Полученное значение τ сравнивается затем со значением табличным (см. табл. 1 приложения) - τ_т, высчитанным для однопроцентного уровня значимости. Если эмпирическое значение τ>τ_т, то исследуемая варианта исключается из данной совокупности, т. е. не используется при дальнейшей обработке.

Пример № 3. В эксперименте по измерению (ВР) времени реакции (см. работу № 16 в гл. II) результаты испытуемого (в сек) по одной и той же задаче составили после упорядочения такой ряд: 0,12; 0,13; 0,15; 0,15; 0,18; 0,20; 0,22; 0,25; 0,28; 0,41; n=10.

Проверим варианту x_n=0,41:

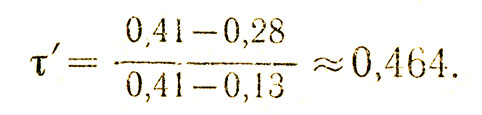
Так как τ_т (табличное) = 0,597, проверяемую варианту нельзя отбросить, т- е. не следует считать данное значение времени реакции случайным.

8-2. Значительно более строгим (и трудоемким) приемом проверки принадлежности к выборке крайних ее членов является знаменитое правило 3-x σ (трех сигм). Оно основано на том, что в интервале M±3σ (см. табл. 12) располагается 99,7% всех вариант, образующих нормальное статистическое распределение. Значит, при допущении такого распределения и после соответствующих вычислений M и σ можно отбросить варианты, меньшие, чем M-3σ, и большие, чем M+3σ, как чрезвычайно маловероятные,

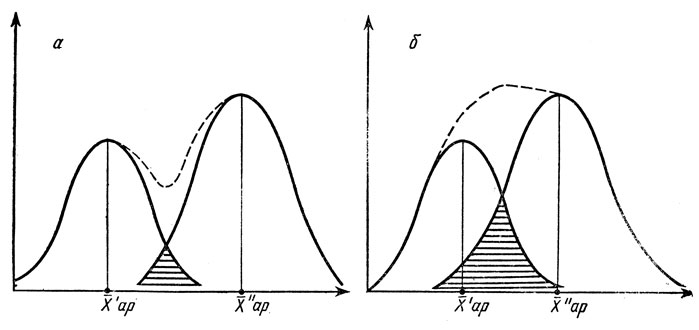
Рис. 21. Схематическая иллюстрация большей (б) или меньшей (а) степени близости двух эмпирических нормальных распределений со средними значениями X'_ap и X"_ap