9. Критерии Стьюдента (t-критерий)

Одной из распространеннейших задач количественной обработки в психологии является задача проверки значимости различия двух средних значений разных статистических совокупностей. Иначе говоря, являются ли две рассматриваемые выборки представителями разных генеральных совокупностей? Существенны ли количественные различия средних значений и правомерны ли выводимые отсюда различия сугубо качественные?

Критерий Стыодента (Госсета) предполагает нормальные распределения в выборках, различия средних значений которых проверяются на статистическую значимость. Этот критерий основан как бы на оценке общих частей двух статистических совокупностей (см. рис. 21), т. е. включает в себя "измерение" и разницы средних значений и мер их разброса.

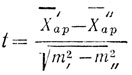
где m=σ/√N есть так называемая ошибка средней, происходящая от представления X_ap в качестве средней M некоторой генеральной совокупности;

X'_ap и X"_ap - средние арифметические, различия между которыми проверяются;

m' и m" - соответствующие ошибки средних,

Пример вычисления t - критерия. Сопоставим данные примера № 2 (по табл. 10) с данными примера № 4 (вторая проба при выработке двигательного навыка - работа № 14 в гл. II).

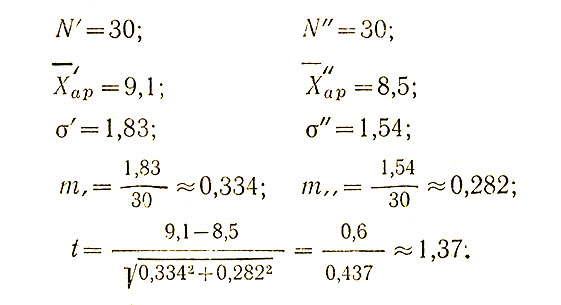
Далее, это значение t=1,37 следует сравнить с табличным значением (табл. II приложения), вычисленным для соответствующей "степени свободы" f, за которую принимается сумма объемов сравниваемых выборок, уменьшенная на две единицы:

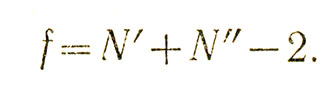
Итак, в нашем случае f=30+30-2=58. По табл. II приложения находим, что значение t для пятипроцентного уровня значимости (даже для f=60) есть t_0,05= 2,0. Так как l,37<t0,05, различия между средними значениями примеров № 2 и 4 не являются статистически значимыми, т. е. убыстрение среднего времени выполнения задания во второй пробе (по сравнению с первой пробой) не является достоверным.

Это не равносильно, конечно, утверждению о статистической однородности двух сопоставляемых выборок. К тому же применение критерия Стьюдента в случае данных скошенных выборок (см. рис. 16) не вполне корректно математически и, бесспорно, сказывается на конечном выводе о недостоверности различий X'_ap=9,1 и X"_ap=8,5. Вообще этот критерий оценивает не степень близости двух средних как таковую, а рассматривает эту близость с точки зрения отнесения или неотнесения ее к случайной (при заданном уровне значимости).