12-5. Парный критерий Вилкоксона

12-5. Парный критерий Вилкоксона (T - критерий) направлен, как и предшествующий критерий знаков, на сравнение величин двух попарно сопряженных совокупностей, но является критерием более мощным, поскольку учитывает не только направление (знак) разности между сравниваемыми рядами, но и абсолютную величину этих разностей T (табл. IX приложения).

Применим этот критерий для примера № 12, для чего следует повторить процедуру вычитания чисел нижнего ряда из верхнего, фиксируя не только знак разности, но и ее величину.

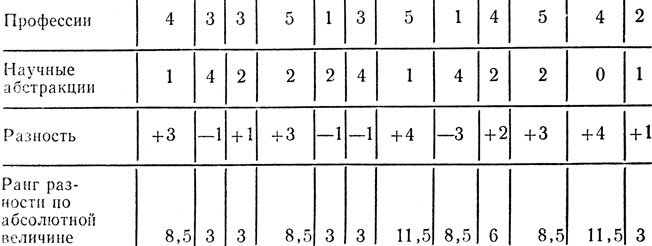
Таблица 21

Далее нужно приписать всем разностям - независимо от знака - их ранг в порядке возрастания величины разности. Результаты такого ранжирования даны в нижней строке табл. 21. Поясняем эту операцию. Самая маленькая величина разности - это 1, но таких единиц всего пять, значит, это будут ранги: 1, 2, 3, 4, 5. Поэтому всем единицам мы проставляем один и тот же ранг 3, отчего общая сумма рангов пяти единиц не изменится. Следующий ранг - 6 получает величина 2. На ранги 7, 8, 9, 10 претендуют четыре величины 3, поэтому все они помечаются рангом 8, 5. Наконец, ранги 11 и 12 выпадают на две величины 4, так что каждая четверка обозначается рангом 11,5.

Теперь подсчитаем сумму рангов Т для отрицательных разностей: T=3+3+3+8,5=17,5.

По табл. IX приложения находим, что T₀₅(12)=17, т, е, наше эмпирическое значение больше табличного для 5-процентного уровня, поэтому различия в величинах объема запоминания разных качеств слов не являются в данной группе испытуемых достоверными.