2. Первоначальная обработка исходного материала

Итак, полученная в измерении статистическая совокупность несет в себе максимум сведений об исследуемом процессе, которые должны быть далее проанализированы с целью получения характеристики объекта исследования. В принципе, каждая варианта выборки имеет определенное право представлять собой изучаемый процесс. Поэтому весь исходный эмпирический материал, имеющийся в виде выборки, должен быть вначале упорядочен, т. е. сведен к некоторой удобной для обозрения и дальнейшего осмысливания форме.

2-1. Упорядочивание - это некоторый исходный этап первоначальной обработки, состоящий в расположении вариант выборки в какой-либо последовательности, удобной для дальнейшего анализа и рассмотрения.

Пример № 1. В эксперименте по заучиванию ряда из десяти двузначных чисел (работа № 10 в гл. II) результаты заучивания после первого предъявления составили для 35 испытуемых следующие величины: 5, 3, 5, 5, 4, 3, 3, 4, 1, 4, 5, 4, 4, 3, 4, 5, 3, 3, 4, 5, 4, 2, 3, 2, 4, 2, 4, 3, 4, 3, 3, 4, 2, 4, 5.

Упорядочив варианты по степени их возрастания, получаем следующий статистический ряд: 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5.

2-2. Вслед за упорядочением вариант часто производят их группировку. Для случаев непрерывной переменной, т. е. такой единицы измерения, которая может иметь дробные значения (в отличие от дискретной переменной, подобной нашему примеру № 1), группировка - это объединение вариант в интервалы, границы которых устанавливаются произвольно и непременно указываются. Такие интервалы могут быть и неравномерными. Срединное значение, или центр интервала, берется обычно числом целым.

2-3. Следующим этапом, логически вытекающим из двух предшествующих, является табулирование, т. е. построение таблиц или собственно статистических распределений, в которых каждой варианте x_i поставлена в соответствие ее частота f_i в выборке или принеобходимости - частость ω_i.

Пример № 2. В эксперименте по выработке двигательного навыка (работа № 14 в гл. II) результаты первой пробы для 30 испытуемых (после упорядочивания) имеют вид такого статистического ряда (в сек.): 5,3; 5,9; 6,2; 6,6; 6,8; 7,0; 7,3; 7,7; 7,8; 7,8, 7,9; 8,1; 8,3; 8,4; 8,6; 8,6; 8,8; 8,9; 9,3; 9,5; 9,7; 10,3; 10,6; 11,0; 11,4; 11,6; 11,9; 12,6; 13,1; 13,9.

Произведя группировку и табулирование, получаем следующее статистическое распределение:

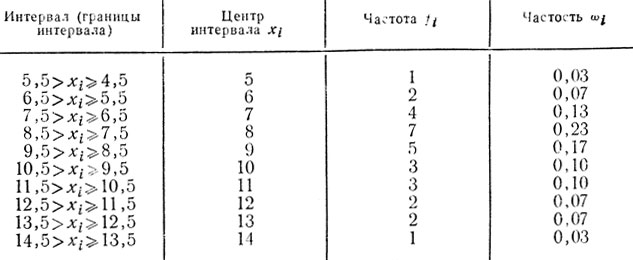
Таблица 1

N=30

Конечно, такая классификация вариант в искусственные интервалы искажает исходную выборку и требует введения особой поправки на непрерывность интервала при последующих вычислениях (см. литературу к гл. III).

Для примера № 1 статистическое распределение таково:

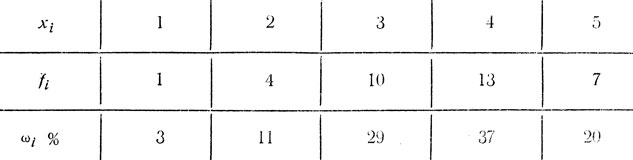
Таблица 2

N=35

2-4. Следующим этапом первоначальной обработки выступает графическое представление статистического распределения. В математической статистике принято два вида графических представлений:

а) полигон (или многоугольник) частот - это ломаная линия, соединяющая точки, соответствующие величинам частот, откладываемым по оси ординат; это единственный способ графического изображения дискретных статистических распределений;

б) гистограмма - график, имеющий вид прямоугольников, основание которых (по оси абсцисс) соответствует интервалу, а высота - частоте (частотному интервалу); площадь гистограммы (в единицах оси ординат) равна, таким образом, общему объему выборки N; графическое представление в этой форме предпочтительнее полигону частот в случае неравномерных интервалов и резких колебаний f_i.

На рис. 15 дан полигон частот для примера № 1 (по результатам табл. 2). На рис. 16 построены гистограмма и полигон частот для примера № 2 (по данным табл. 1).

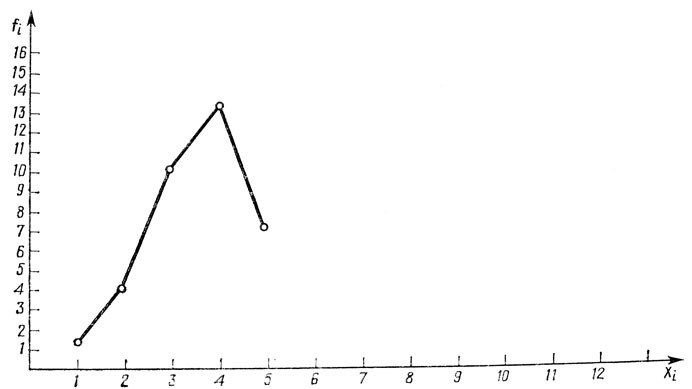
Рис. 15. Полигон частот для примера № 1

Помимо указанных, могут оказаться полезными графические представления в виде различных диаграмм, например круговых.

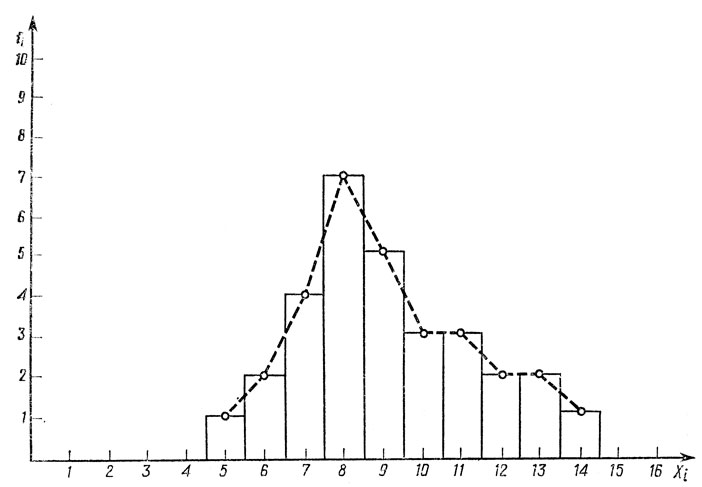
Рис. 16. Гистограмма и полигон частот (пунктиром) для примера № 2