12-1. Критерий χ2 (хи-квадрат)

12-1. Критерий χ² (хи-квадрат) используется для сравнения частот двух распределений: двух эмпирических или эмпирического и теоретического.

Применение критерия требует, чтобы объем сопоставляемых распределений был не менее 20-30 вариант, а минимальная их частота - не менее пяти (в противном случае следует произвести укрупнение разрядов).

Формула критерия χ² такова:

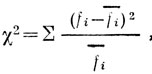
где f_i - каждая частота двух сопоставляемых выборок, соответствующая единому аргументу;

f_i - среднее значение данной частоты по двум выборкам (или ожидаемая частота).

При сопоставлении двух эмпирических выборок вычисления упрощаются, если формулу χ² преобразовать таким образом:

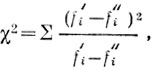
где f'_i и f"_i - частоты двух сопоставляемых выборок.

Полученная сумма сравнивается с табличным значением для того или иного уровня значимости (таблица V приложения).

Примеры № 9 и 10.

При заучивании двузначных чисел (работа № 10 в гл. II) в двух группах испытуемых при втором предъявлении заучиваемого ряда получены такие результаты:

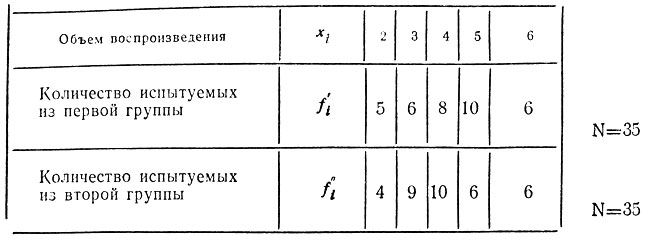
Вопрос: значимо ли различие частот в этих двух группах? Число составляемых разрядов f=5.

Вычисление χ² приводим в таблице (по упрощающей формуле).

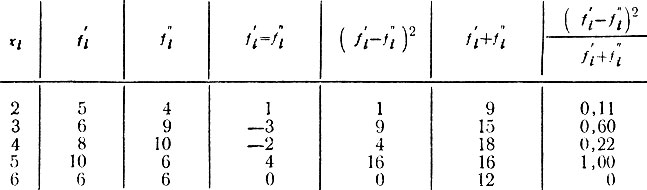
Таблица 17

В табл. V приложения даны соответствующие значения χ², где к - число степеней свободы, определяемое как уменьшенное на единицу количество сопоставляемых разрядов f.

к=f-1=5-1=4.

Так как табличное значение χ²₀₅ (4)=9,49 и вычисленное эмпирическое 1,93<χ²₀₅, значит> различий менаду частотами в двух группах испытуемых нет, обе эмпирические совокупности можно считать выборками из одной генеральной совокупности.