12-3. Критерий числа инверсий

12-3. Критерий числа инверсий (Вилкоксона - Манна - Уитни) предназначен (как и серийный критерий) для оценки различия величин членов двух выборок, но является более мощным.

Этот критерий основан на подсчете числа инверсий U (перестановок, нарушений порядка расположения) членов в их общем упорядоченном ряду. Общая сумма инверсий сравнивается с табличной (табл. VII приложения).

Применим этот критерий для нашего примера № 11.

Первый шаг работы полностью аналогичен осуществленному для серийного критерия, т. е. составляется общий упорядоченный ряд. Таким образом, повторяется таблица 18.

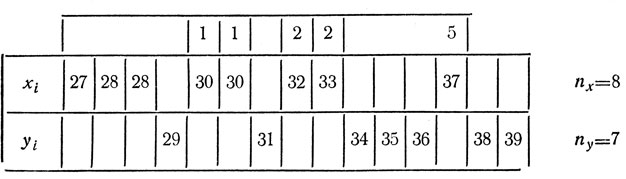
Таблица 19

Теперь нужно подсчитать число инверсий U, т. е. для нашего случая число нарушений того порядка расположения членов, при котором члены верхнего ряда x_i идут впереди членов второго ряда y_i. Соответствующие цифры удобнее проставлять над числами верхнего ряда.

Перед числами 30, 30 впереди идет одно число 29 из нижнего ряда, поэтому сверху проставлено по единице. Перед числами 32 и 33 величин x_i вперед попадают уже два числа y_i (29 и 31), поэтому над величинами 32 и 33 проставлены двойки. Наконец, числу 37 верхнего ряда предшествует уже 5 чисел ряда нижнего.

Общее число инверсий U=1+1+2+2+5=11. По табл. VII приложения находим, что U₀₅(8,7)=12, так что можно считать различия величин порогов мужчин и женщин статистически значимыми для пятипроцентного уровня значимости (P=0,05).